题目
只允许利用numpy包,实现Pytorch二维卷积函数nn.Conv2d()
解答
此代码考察二维卷积的概念,详见:
6.2. 图像卷积 — 动手学深度学习 2.0.0 documentation
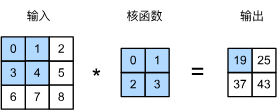
6.3. 填充和步幅 — 动手学深度学习 2.0.0 documentation


6.4. 多输入多输出通道 — 动手学深度学习 2.0.0 documentation

代码实现:
import numpy as np
import torch
import torch.nn as nn
def conv2d(input, weight, bias=None, stride=1, padding=0):
"""
实现二维卷积操作
参数:
input: 输入数据, 形状为 (batch_size, in_channels, height, width)
weight: 卷积核, 形状为 (out_channels, in_channels, kernel_h, kernel_w)
bias: 偏置项, 形状为 (out_channels,)
stride: 步长, 可以是整数或元组 (stride_h, stride_w)
padding: 填充, 可以是整数或元组 (pad_h, pad_w)
返回:
输出特征图, 形状为 (batch_size, out_channels, out_h, out_w)
"""
# 解析步长和填充参数
if isinstance(stride, int):
stride_h = stride_w = stride
else:
stride_h, stride_w = stride
if isinstance(padding, int):
pad_h = pad_w = padding
else:
pad_h, pad_w = padding
# 获取输入尺寸
batch_size, in_channels, in_h, in_w = input.shape
out_channels, _, kernel_h, kernel_w = weight.shape
# 计算输出尺寸
out_h = (in_h + 2 * pad_h - kernel_h) // stride_h + 1
out_w = (in_w + 2 * pad_w - kernel_w) // stride_w + 1
# 添加填充
if pad_h > 0 or pad_w > 0:
# 使用零填充
padded_input = np.pad(
input,
((0, 0), (0, 0), (pad_h, pad_h), (pad_w, pad_w)),
mode='constant'
)
else:
padded_input = input
# 初始化输出数组
output = np.zeros((batch_size, out_channels, out_h, out_w))
# 执行卷积操作
for b in range(batch_size):
for c_out in range(out_channels):
for h_out in range(out_h):
for w_out in range(out_w):
# 计算输入窗口位置
h_start = h_out * stride_h
w_start = w_out * stride_w
h_end = h_start + kernel_h
w_end = w_start + kernel_w
# 提取输入窗口
window = padded_input[b, :, h_start:h_end, w_start:w_end]
# 计算点积 (卷积操作)
conv_val = np.sum(window * weight[c_out])
# 添加偏置
if bias is not None:
conv_val += bias[c_out]
# 存储结果
output[b, c_out, h_out, w_out] = conv_val
return output
import torch
import torch.nn as nn
if __name__ == "__main__":
# 创建测试数据
np.random.seed(42)
# 输入数据: (batch_size=2, in_channels=3, height=5, width=5)
input_data = np.random.randn(2, 3, 5, 5).astype(np.float32)
# 卷积核: (out_channels=2, in_channels=3, kernel_h=3, kernel_w=3)
weights = np.random.randn(2, 3, 3, 3).astype(np.float32)
# 偏置: (out_channels=2)
bias = np.array([0.5, -0.5], dtype=np.float32)
# 转换为 PyTorch 张量
input_torch = torch.tensor(input_data)
weights_torch = torch.tensor(weights)
bias_torch = torch.tensor(bias)
# 测试1: 无填充, 步长=1
print("测试1: 无填充, 步长=1")
output1 = conv2d(input_data, weights, bias, stride=1, padding=0)
# 创建 PyTorch 卷积层
conv1_nn = nn.Conv2d(in_channels=3, out_channels=2, kernel_size=3,
stride=1, padding=0, bias=True)
# 设置权重和偏置
with torch.no_grad():
conv1_nn.weight.data = weights_torch
conv1_nn.bias.data = bias_torch
# 计算 PyTorch 输出
output1_nn = conv1_nn(input_torch).detach().numpy()
# 比较结果
print("自定义实现与PyTorch输出是否一致:", np.allclose(output1, output1_nn, atol=1e-6))
print(f"输出形状: {output1.shape}")
print("自定义实现输出 (第一个样本的第一个通道前2x2):")
print(output1[0, 0, :2, :2])
print("PyTorch输出 (第一个样本的第一个通道前2x2):")
print(output1_nn[0, 0, :2, :2])
# 测试2: 填充=1, 步长=1
print("\n测试2: 填充=1, 步长=1")
output2 = conv2d(input_data, weights, bias, stride=1, padding=1)
# 创建 PyTorch 卷积层
conv2_nn = nn.Conv2d(in_channels=3, out_channels=2, kernel_size=3,
stride=1, padding=1, bias=True)
with torch.no_grad():
conv2_nn.weight.data = weights_torch
conv2_nn.bias.data = bias_torch
output2_nn = conv2_nn(input_torch).detach().numpy()
print("自定义实现与PyTorch输出是否一致:", np.allclose(output2, output2_nn, atol=1e-6))
print(f"输出形状: {output2.shape}")
print("自定义实现输出 (第一个样本的第一个通道前2x2):")
print(output2[0, 0, :2, :2])
print("PyTorch输出 (第一个样本的第一个通道前2x2):")
print(output2_nn[0, 0, :2, :2])
# 测试3: 无填充, 步长=2
print("\n测试3: 无填充, 步长=2")
output3 = conv2d(input_data, weights, bias, stride=2, padding=0)
# 创建 PyTorch 卷积层
conv3_nn = nn.Conv2d(in_channels=3, out_channels=2, kernel_size=3,
stride=2, padding=0, bias=True)
with torch.no_grad():
conv3_nn.weight.data = weights_torch
conv3_nn.bias.data = bias_torch
output3_nn = conv3_nn(input_torch).detach().numpy()
print("自定义实现与PyTorch输出是否一致:", np.allclose(output3, output3_nn, atol=1e-6))
print(f"输出形状: {output3.shape}")
print("自定义实现输出 (第一个样本的第一个通道):")
print(output3[0, 0])
print("PyTorch输出 (第一个样本的第一个通道):")
print(output3_nn[0, 0])
# 测试4: 无偏置
print("\n测试4: 无偏置")
output4 = conv2d(input_data, weights, None, stride=1, padding=0)
# 创建 PyTorch 卷积层
conv4_nn = nn.Conv2d(in_channels=3, out_channels=2, kernel_size=3,
stride=1, padding=0, bias=False)
with torch.no_grad():
conv4_nn.weight.data = weights_torch
output4_nn = conv4_nn(input_torch).detach().numpy()
print("自定义实现与PyTorch输出是否一致:", np.allclose(output4, output4_nn, atol=1e-6))
print("自定义实现输出 (第一个样本的第一个通道前2x2):")
print(output4[0, 0, :2, :2])
print("PyTorch输出 (第一个样本的第一个通道前2x2):")
print(output4_nn[0, 0, :2, :2])
'''
测试1: 无填充, 步长=1
自定义实现与PyTorch输出是否一致: True
输出形状: (2, 2, 3, 3)
自定义实现输出 (第一个样本的第一个通道前2x2):
[[-6.4546895 -2.49435902]
[-6.27663374 3.31103873]]
PyTorch输出 (第一个样本的第一个通道前2x2):
[[-6.4546895 -2.4943593]
[-6.276634 3.3110385]]
测试2: 填充=1, 步长=1
自定义实现与PyTorch输出是否一致: True
输出形状: (2, 2, 5, 5)
自定义实现输出 (第一个样本的第一个通道前2x2):
[[ 1.17402518 1.28695214]
[-0.09722954 -6.4546895 ]]
PyTorch输出 (第一个样本的第一个通道前2x2):
[[ 1.1740253 1.2869523 ]
[-0.09722958 -6.4546895 ]]
测试3: 无填充, 步长=2
自定义实现与PyTorch输出是否一致: True
输出形状: (2, 2, 2, 2)
自定义实现输出 (第一个样本的第一个通道):
[[-6.4546895 1.38441801]
[ 3.1934371 -1.1537782 ]]
PyTorch输出 (第一个样本的第一个通道):
[[-6.4546895 1.3844179]
[ 3.1934366 -1.1537789]]
测试4: 无偏置
自定义实现与PyTorch输出是否一致: True
自定义实现输出 (第一个样本的第一个通道前2x2):
[[-6.9546895 -2.99435902]
[-6.77663374 2.81103873]]
PyTorch输出 (第一个样本的第一个通道前2x2):
[[-6.9546895 -2.9943593]
[-6.776634 2.811039 ]]
'''