
在之前的文章中,我们介绍了永磁同步电机无感控制中的滑模观测器,但是同时我们也认识到了他的缺点:因符号函数带来的高频切换分量,使用低通滤波器引发相位延迟;在本篇文章,我们将会介绍高阶滑模观测器的无感控制策略,该种方案拥有不需要经过低通滤波器的优势,收敛速度更快,能够增强观测精度,通过构造更复杂的滑模面,引入额外的滑膜增益项,可以有效地抑制外部噪声、系统参数变化等不确定性,拥有更强的鲁棒性。
目录
一.高阶状态变量
(1)一阶状态变量
(2)“高阶”状态变量
二.永磁同步电机数学模型
(1)永磁同步电机在两相静止坐标系下的数学模型为:
(2)扩展电动势
三.高阶滑模观测器设计
六.Simulink仿真
一.高阶状态变量
状态变量是用来描述系统动态行为的一组变量,通常构成状态空间模型的基础。而状态变量本身都是通过一阶微分方程来描述的,不管原系统是几阶。
(1)一阶状态变量
一阶系统由单个一阶微分方程描述,仅需一个状态变量。例如:

仅含一个状态变量 x
(2)“高阶”状态变量
高阶系统(如n阶微分方程)通过引入多个一阶状态变量来简化。例如二阶系统可简化:
![]()
可分解为:

对应的状态方程:

这里的“高阶”指原系统的微分方程阶数(如二阶、三阶),而非状态变量本身。指通过增加状态变量的数量来处理高阶系统,其每个状态变量仍是一阶的,但数量与系统阶数相等。
在传统的滑膜观测器设计中,其状态估计变量是电流,而在我们的高阶滑膜观测器中,其状态估计变量除了电流,还有我们的反电动势。在后面会对其原理和设计进行介绍。
二.永磁同步电机数学模型
(1)永磁同步电机在两相静止坐标系下的数学模型为:

---式(1)
(2)扩展电动势(electromotive force,EMF)可以写为如下形式:

---式(2)
三.高阶滑模观测器设计
设计我们高阶滑膜观测器的前提是,机械时间常数远大于电气时间常数,故ωe的导等于0;或者可以这么理解,在mcu的一个很短的控制周期内,速度变化量小,ωe的导约等于0。
所以我们可将式(2)求导并化简得到:



---式(3)
将式(1)的电流状态变量和式(3)的EMF作为高阶状态变量描述如下:

---式(4)
式(4)中![]()
基于上式,我们设计高阶滑膜观测器为:
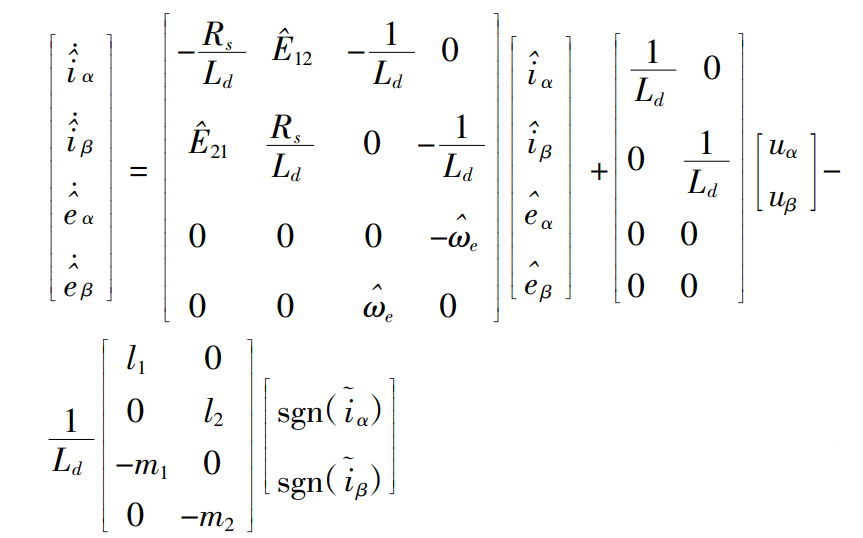
将上矩阵展开得到:

---式(5)
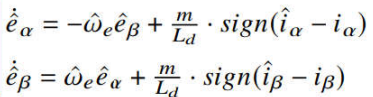
在滑模面附近,有 ,所以带入式(5)中,两个不连续的高频切换控制分量可以等效表示为:
,所以带入式(5)中,两个不连续的高频切换控制分量可以等效表示为:

将上式代入式(5)的后两式,可得:

---式(6)
由此可见,由于我们将符号函数用等效表示替代,式中没有出现因符号函数带来的高频切换分量。因此,使用高阶滑模观测器估计的角速度不需要经过低通滤波器,简化了控制系统结构。
将公式编码到MCU迭代计算,调整增益矩阵中的参数使得观测器收敛,可得到反电动势矩阵![]() 反电动势中包含θe的信息,对其提取可得到速度与角度。当采用id=0控制时,有:
反电动势中包含θe的信息,对其提取可得到速度与角度。当采用id=0控制时,有:

根据反电动势求解出电角度:![]()
在经过PLL角度速度提取,即可得到角速度和电角度:

注:EEMF的收敛速度与转速密切相关,固定的滑模增益不能确定固定的系统阻尼。
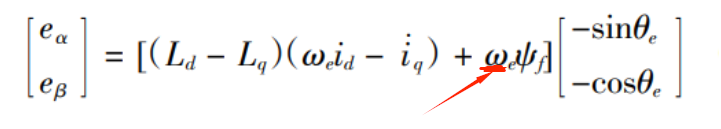
后续还可以归一化PLL,使得观测角度与实际角度的传递函数根轨迹不再与转速相关,在本篇文章中暂且不予说明。
六.Simulink仿真
我们对式(5)式(6)进行建模,并在离散状态下迭代计算:



仿真中的模型Equ1-4分别对应着4个公式





其仿真数据检查器分别是:
1.估计角速度---真实角速度
2.估计电角度和真实电角度
3.αβ反电动势
4.电机三相电流





















