知识总览

生成树(一定是连通的):
是连通的无向图的一个子图,子图包含这个无向图的所有顶点+有n-1条边(少一条边,生成树就不连通了)即为生成树,一个连通图可能有多个生成树

最小生成树(最小代价树):
只有连通的无向图才有生成树,不连通的无向图有多个连通分量,每个连通分量有生成树,合起来叫生成森林,单个的不连通的无向图没有生成树
如果一个连通的无向图本身就是一棵树,那最小生成树就是它本身




求最小生成树:
同一个图可能有多个最小生成树,虽然形态不同,但是生成的最小生成树的各个边的权值之和都是最小的

prim(普里姆算法):
概念:
从任意一个顶点出发构建最小生成树,每次都把权值最小的边连接的顶点纳入到生成树里,直到所有顶点都被纳入进去
过程:
假设从如下P城出发开始构建生成树,此时生成树里只有P城顶点,与P城相连的权值最小的顶点为学校1,把P城->学校边标红,此时生成树里的顶点有P城、学校,与P城、学校相连的权值最小的边是矿场或渔村都是4,假设选择矿场把P城->矿场边标红,此时生成树里的顶点有P城、学校、矿场,与P城、学校、矿场相连的权值最小的边为渔村2,生成树里的顶点有P城、学校、矿场、渔村,把矿场->渔村边标红,与P城、学校、矿场、渔村相连的权值最小的边为农场5,生成树里的顶点有P城、学校、矿场、渔村、农场,把P城->农场边标红,与P城、学校、矿场、渔村、农场相连的权值最小的边为电站3,把农场->电站边标红,生成树里的顶点有P城、学校、矿场、渔村、农场、电站。至此所有顶点纳入到生成树,最小生成树生成,权值为各边权值之和1+4+2+5+3=15
假设从如下P城出发开始构建生成树,此时生成树里只有P城顶点,与P城相连的权值最小的顶点为学校1,把P城->学校边标红,此时生成树里的顶点有P城、学校,与P城、学校相连的权值最小的边是矿场或渔村都是4,假设选择渔村把P城->渔村边标红,此时生成树里的顶点有P城、学校、渔村,与P城、学校、渔村连的权值最小的边为矿场2,生成树里的顶点有P城、学校、矿场、渔村,把渔村->矿场边标红,与P城、学校、渔村、矿场相连的权值最小的边为农场5,生成树里的顶点有P城、学校、渔村、矿场、农场,把P城->农场边标红,与P城、学校、渔村、矿场、农场相连的权值最小的边为电站3,把农场->电站边标红,生成树里的顶点有P城、学校、渔村、矿场、农场、电站。至此所有顶点纳入到生成树,最小生成树生成,权值为各边权值之和1+4+2+5+3=15
两个从P城出发的最小生成树形态不同,但是权值之和一样,即一个图的最小生成树有多个
如图(最后一个图)为从农场出发的最小生成树,最后权值之和=15




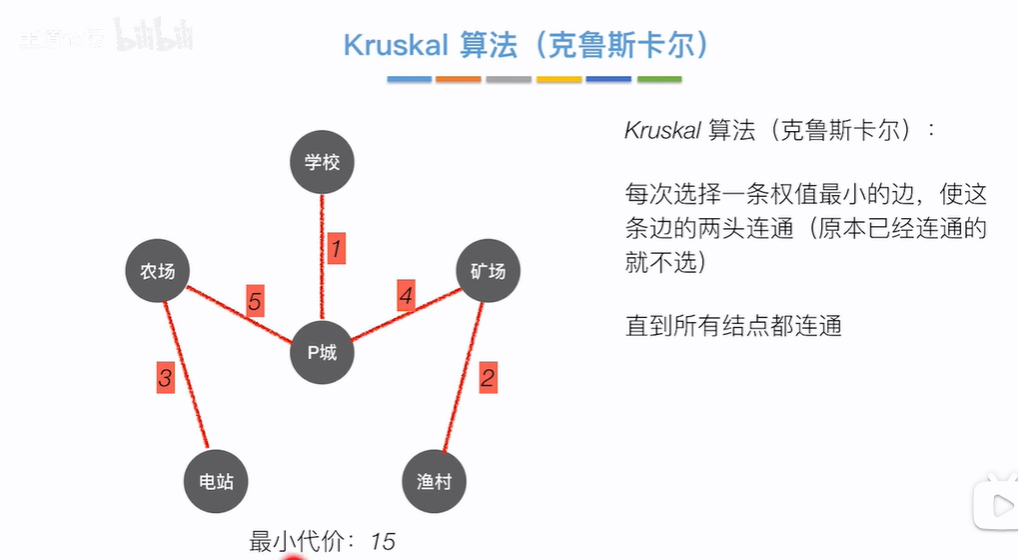
Kruskal(克鲁斯卡尔算法):
注意连通不是2个顶点直接相连,而是有从一个顶点到另外一个顶点的路径,即A、B、C三个顶点,A->B->C也叫做A和C连通
概念:
每次都找权值最小的边,直到所有的边对应的2个顶点都连通(有路径,不是直接相连)
过程:
各个顶点没有连通所以是虚线,每次选权值最小的边,如下图开始权值最小为1,即把P城和学校标红连通,去掉权值1,然后剩余权值最小为2即把矿场和渔村标红连通,去掉权值2,剩余权值最小为3即把农场和电站标红连通,去掉权值3,剩余权值最小为4即P城和矿场或者P城和渔村,假设选择P城和矿场即把P城和矿场标红连通,去掉权值4,剩余权值最小为4,但是P城和渔村已经连通,即P城->矿场->渔村,故去掉P城->渔村权值4,剩余权值最小为5,即把矿P城和农场标红连通,此时如下图所有节点都已连通,最小生成树生成,权值之和为1+2+3+4+5=15跟普利姆算法同
如下所示假如先选择P城和渔村相连最后最小生成树形态和上述不同,但是权值之和应该还是15


普里姆算法和克鲁斯卡尔算法比较:
普里姆算法是从顶点开始,致力于把顶点都纳入到生成树,时间复杂度只和顶点有关系为O(v²),适用于边稠密图(为啥?因为边稠密可能顶点少,时间复杂度低,跟邻接矩阵差不多?),克鲁斯卡尔算法是每次找边,致力于把边都连通,时间复杂度只和边有关系为O(Elog2|E|),适用于边稀疏图(因为边稀疏时间复杂度低)
普利姆算法时间复杂度:每次都要把一个未加入生成树的顶点加入到生成树,共有n个顶点遍历n-1次,每次遍历的时候要再遍历一遍lowCost数组去处理各个顶点的最小代价,所以是双层for循环,所以时间复杂度是O(v²)【大概是吧,想不出来。。。。。】
克鲁斯卡尔算法时间复杂度:每次都要用并查集遍历所有的边查询变对应的2个顶点是否属于一个集合,不是一个集合就把2个顶点边标红放到生成树,假设边数为e,每条边使用并查集时间开销为log2e,则一共时间复杂度是O(elog2e)。。。。。。。。。



prim普利姆算法实现思想:
时间开销计算在上边
初始化:2个数组,isJoin数组记录已经加入生成树的节点,lowCost数组记录要加入当前生成树各个节点花费的代价,初始化时vo已经加入生成树,其他顶点还没加入生成树,vo和v1直接相连有一条边权值为6,则加入当前生成树V1花费代价为6,v0和V2相连边上的权值为5,则v2加入当前生成树花费代价为5,同理v3代价为1,v4和v5并不和v0直接相连,所以认为花费代价是∞
第一轮处理:循环遍历isJoin数组找到没加入生成树的节点+从lowCost数组找到未加入节点花费最小的节点加入生成树,由初始化过程知道没加入+加入花费最小节点为V3,即把V3加入节点,修改剩余未加入生成树节点的最小花费代价,目前V0、V3已加入生成树,v3和v1相连花费代价为5,比v0和v1相连代价6要小,更新v1加入生成树代价为5,v3和v2相连权值为4比v0和V2相连代价5小,更新v2加入生成树代价为4,v3和V4相连权值为6比V0和V4不相连代价∞小,更新v4加入生成树代价为6,同理更新V5加入生成树代价为4
第二轮:上同第一轮
第三轮:上同第一轮
第4轮:上同第一轮
第5轮:上同第一轮
![]()
![]()
![]()
![]()
![]()
![]()
![]()
卡鲁斯卡尔算法思想:
时间开销计算在上边
初始化:因为每次找的都是权值最小的边,所以先将各个边按权值大小排序
第一轮:检查第一条边的2个顶点是否连通,不连通连起来,是否连通用并查集判断,听说是开始这俩顶点因为不连通分别属于各个集合,当连通了就把这俩顶点放到一个集合上了,所以集合1{V0,V3}
第2轮:检查第2条边的2个顶点是否连通,不连通连起来,上同第一轮,V2V5开始不连通,连通后放到同一集合{V2,V5}
第3轮:检查第3条边的2个顶点是否连通,不连通连起来,上同第一轮,V1V4开始不连通,连通后放到同一集合{V1,V4}
第4轮:检查第4条边的2个顶点是否连通,不连通连起来,上同第一轮,V2V3开始不连通,连通后放到同一集合{V0,V3,V2}、{V2,V5、V3}
第4轮:检查第5条边的2个顶点是否连通,不连通连起来,上同第一轮,V3V5已经连通,连通的就跳过(因为上边这俩顶点已经在同一个集合了)
第5轮:上同
第6轮:上同,每次都检查该条边连接的2个顶点是否是同一个集合,不是就选上纳入到生成树
![]()
![]()
![]()
![]()
![]()
![]()
![]()
知识回顾:

。。。。。。。。。。。。。。。。