查询

news2025/7/12 13:26:34

一、顺序查询

普通查找方式：

int SeqSearch(int a[],int n,int k)
{
	int i = 0;
	while (i < n && a[i] != k)
		i++;
	if (i >= n)
		return 0;
	else
		return i + 1;
}

优化版查找方式：

int OPSeqSearch(int a[], int n, int k)
{
	int i = 0;
	a[n] = k;
	while (a[i] != k)
		i++;
	if (i == n)
		return 0;
    else
	    return i + 1;
}

两种查询方式的不同点：循环过程是否需要进行 i<n 的判断。

优化方式：在数组的末尾增加了要查找的元素，使每次的循环不需要 i<n 的判断。

节省时间展示：

通过60000000次的查询，优化版的比未优化版大约节省了25ms时间。

附：时间间隔求法

完整代码展示：

//顺序查找
# include <iostream>
# include<time.h>
using namespace std;
int SeqSearch(int a[],int n,int k) //未优化前的顺序查询
{
	int i = 0;
	while (i < n && a[i] != k)
		i++;
	if (i >= n)
		return 0;
	else
		return i + 1;
}
int OPSeqSearch(int a[], int n, int k)  //优化后的顺序查询
{
	int i = 0;
	a[n] = k;
	while (a[i] != k)
	{
		i++;
	}
	if (i == n)
	{
		return 0;
	}
	return i + 1;
}
int main(void)
{
	int a[60000000];
	for (int i = 0; i < 60000000; i++)
	{
		a[i] = i;
	}
	clock_t start, finish, OPstart, OPfinish;
	double duration, OPduration;


	//计算未优化前的执行时间
	start = clock(); 
	SeqSearch(a, 60000000, 59999999);
    finish = clock();

	//优化后的执行时间
	OPstart = clock();
	OPSeqSearch(a, 60000000, 59999999);
	OPfinish = clock();

	duration = (double)(finish - start)/CLOCKS_PER_SEC*1000;
	OPduration= (double)(OPfinish - OPstart)/CLOCKS_PER_SEC*1000;

	printf("未优化前执行60000000次查询需花费：%f ms\n", duration);
	printf("优化后执行60000000次查询需花费：%f ms", OPduration);
	system("pause");
	return 0;
}

平均查找长度：在查找运算中，时间主要花费在关键字比较上，把平均需要关键字比较次数称为平均查找长度。

查找成功的平均查找长度：

$ASL=\sum_{i=1}^{n}p_ic_i$ $=\frac{1}{n}\sum_{i=1}^{n}i=\frac{1}{n}\times \frac{n(n+1)}{2}=\frac{n+1}{2}$

查找失败的平均查找长度：

$ASL=n$

因此此顺序查找算法的平均时间复杂度为O(n) 。

顺序查找：优点是算法简单，且对于表的存储结构五特别的要求，无论是顺序表还是链表也无论是元素之间是否按关键字有用，他都同样适用

缺点是查找效率低。

二、折半查找

1.思路与代码

折半查找又称二分查找，其要求是线性表是有序表，即表中的元素按关键字有序排列。

查找思路：

设 R[low...high] 是当前的查找区间，首先确定该区间的中点位置 mid=[(low+high)/2]，然后将待查的 k 值与 R[mid] 进行比较。

1.若k=R[mid]，则查找成功并返回该元素的逻辑序号。

2. 若k<R[mid]，则由表的有序性可知 R[mid...high] 均大于k，因此若表中存在关键字等于k的元素，则该元素必定在位置mid左边的子表 R[low...mid-1] 中，故新查找的区间是左子表 R[low...mid-1]。

3.若k>R[mid]，则关键字为 k 的元素必定在 mid 的右子表 R[mid+1...high] 中，即新的查找区间是右子表 R[mid+1...high]。

折半查询代码：

int BinSearch(int R[], int n, int k)
{
	int low = 0, high = n - 1, mid;
	while (low <= high)
	{
		mid = (low + high) / 2;
		if (k == R[mid])
			return mid + 1;             //查找成功返回其逻辑序号mid+1
		if (k < R[mid])
			high = mid - 1;             //在R[low...mid-1]中查找
		else
			low = mid + 1;              //在R[mid+1...high]中查找
	}
	return 0;                           //未找到时返回0（查找失败）
}

2.折半查找判定树

折半查找判定树：用来描述折半查找过程的的二叉树叫做判定树或比较树。

设存在有序表R[0...10]={2，7，11，16，21，27，32，45，53，62，78}.则其二叉查找树为：

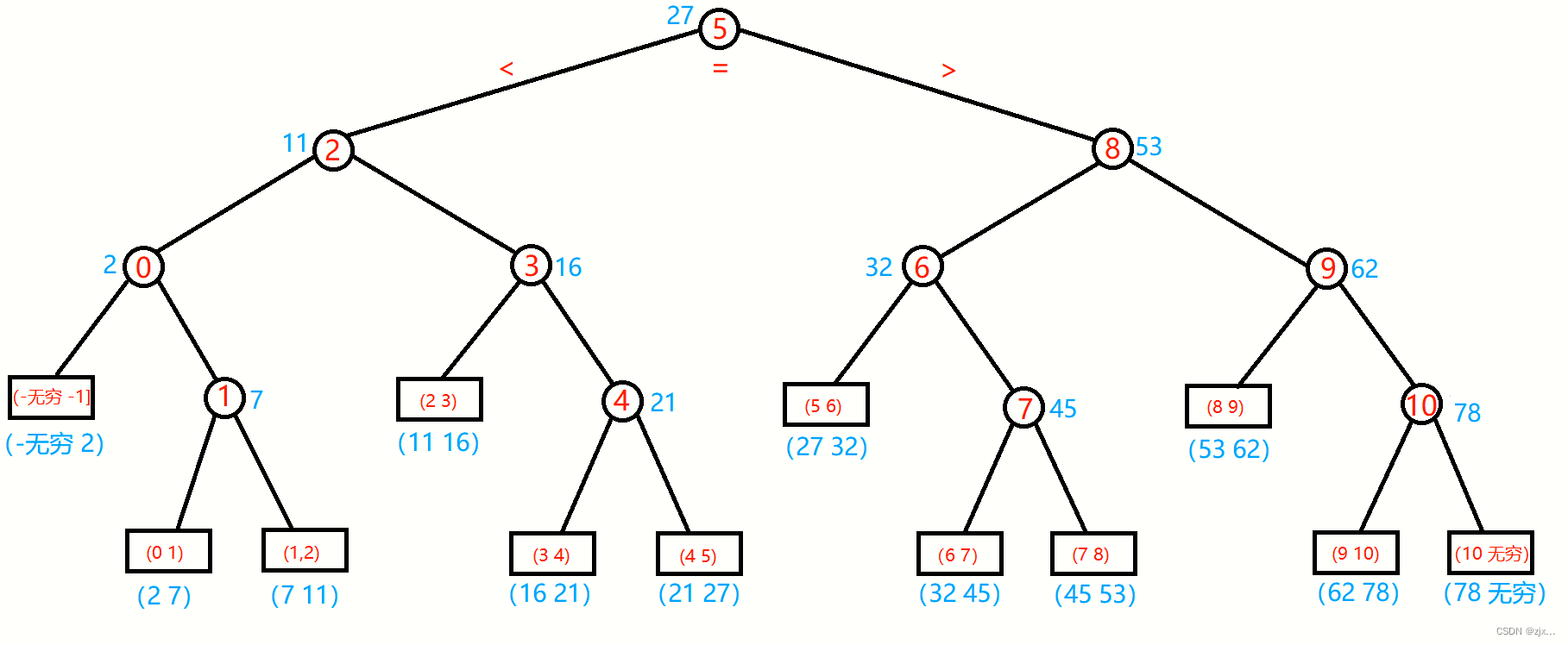
注：

1. 红色字体代表数组下标，蓝色字体代表数组下标对应的值。

2. 圆节点代表可查询到的节点，方块节点代表未在数组中的节点。

3. 蓝色（2 7）代表 2 与 7 之间的数，不包括2与7。

4. 红色（0 1）代表 0 与 1 之间的数组下标，不包括 0 与1。

内部点：树中圆节点个数。

外部点：树中方节点个数。

如果树中有n个内部点，则其有n+1个外部点。

3.平均查找长度与时间复杂度

由折半查找判定树可知，节点的层数即为该节点的查找次数，由此可得成功的二分查找次数是：

$ASL=\frac{1}{n}\sum_{i=1}^{h}c_i\times i$

其中 n 为总结点数（不包括方节点），h 为树的高度，ci 为第 i 层节点的个数。

成功与不成功的最多查找次数为树的高度：

$\left \lceil log_2(n+1) \right \rceil$

综上所述其时间复杂度为

$O(log_2n)$

三、分块查找

1.实现原理

性能介于顺序查找与折半查找之间，通过索引存储结构将整个数组分块，以便于查找。

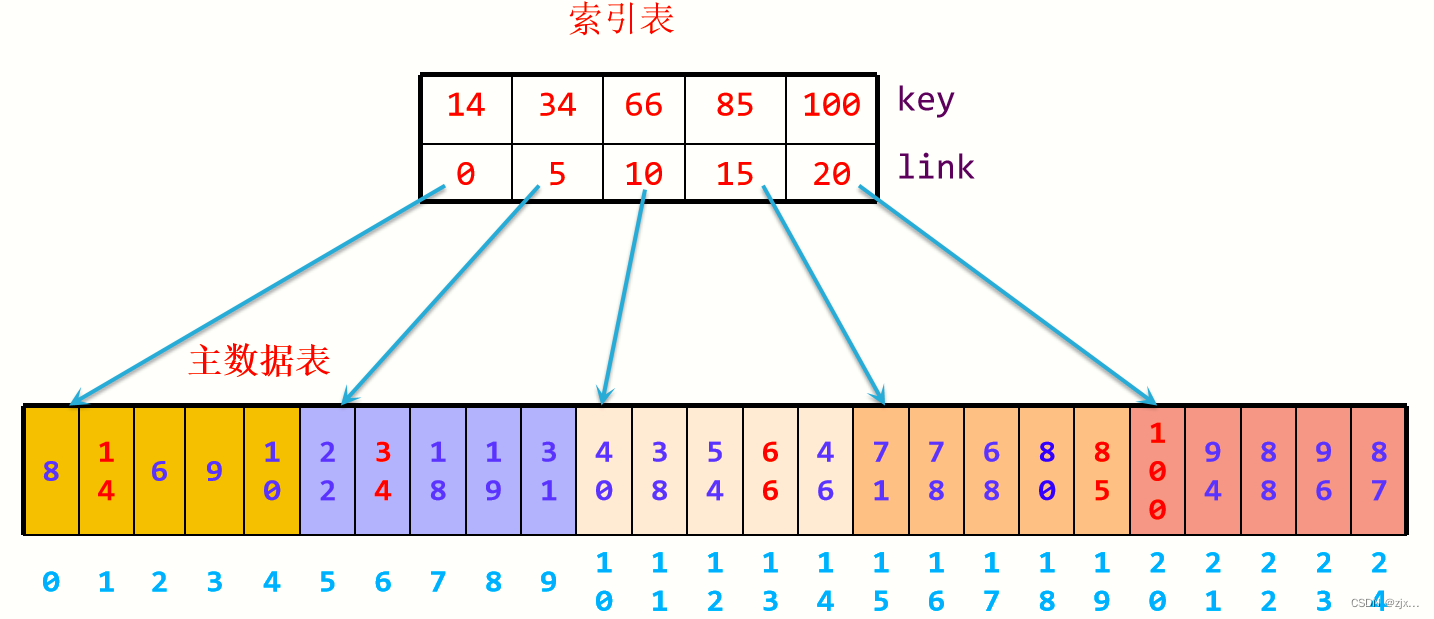
索引表中的 key 值对应主数据表中此块的最大值 ，link 值对应主数据表此块的起始位置下标。

2.实现代码

int IdxSearch(int I[], int R[], int b, int n, int k)
{
	//I为索引表，R为数据表，b为索引表的长度，n为数据表的长度，k为要查找的数据
	int s = (n + b - 1) / b;     //s为每块中的元素个数，应为（n/b）下取整
	int low = 0, high = b - 1, mid, i;
	while (low <= high)                 //采用折半查找，找到的位置为high+1
	{
		mid = (low + high) / 2;
		if (I[mid].key >= k)
			high = mid - 1;
		else
			low = mid + 1;
	}
	i = I[high + 1].link;
	while (i < I[high + 1].link + s && R[i] != k)
		i++;

	if (i <= I[high + 1].link + s - 1)
		return i + 1;              //返回其逻辑序号
	else
		return 0;
}

3.平均查找长度及时间复杂度

设有 n 个元素，每个块中有 s 个元素，索引表长度为b。

折半查找+顺序查找：

$\small ASL=ASL_b+ASL_s= log_2(b+1)-1+\frac{s+1}{2} \approx log_2(\frac{n}{s}+1)+\frac{s}{2}$

s 越小 ASL 的值越小，即当采用折半查找确定块时，每块的长度越小越好。

顺序查找+顺序查找：

$\small ASL=ASL_b+ASL_b=\frac{b+1}{2}+\frac{s+1}{2}=\frac{1}{2}(\frac{n}{s}+s)$

显然，当s= $\small \sqrt{n}$ 时，ASL取极小值 $\small \sqrt{n}+1$ ，故采用此方式查找时选定 $\small \sqrt{n}$ 效果最佳。