1. 置信区间是衡量测量精度的一个指标，也能显示出估算有多稳定，也就是说如果重复做某项实验，得到的结果与最初的估计有多接近。
2. 步骤：
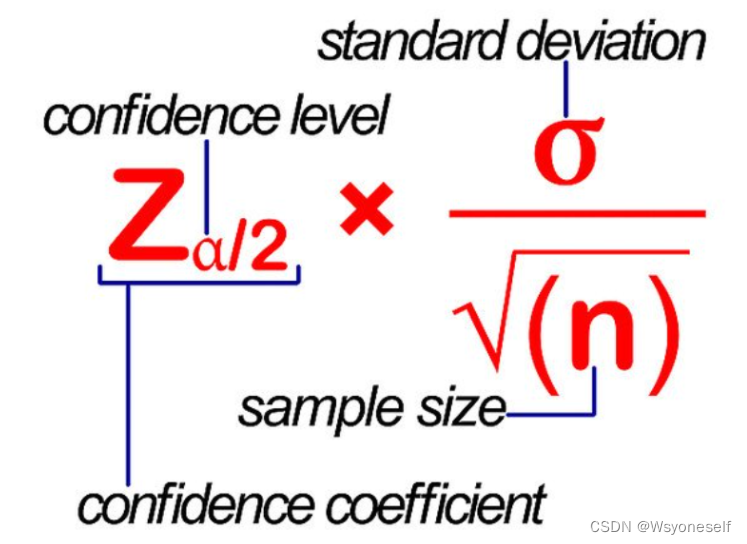
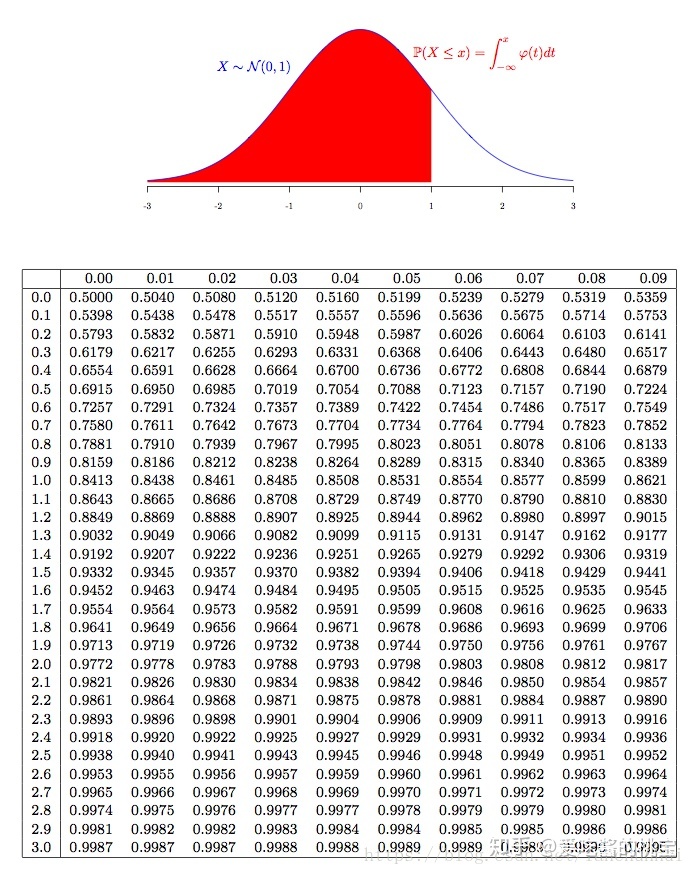
   1. 确定要测试的情况：如“A大学男生的平均体重是80公斤”，则后续就是要测试在给定的置信区间内，能够准确预测A大学男生体重的概率；
   2. 从所选总体中选择一个样本：从总体中抽取数据验证假设；
   3. 计算样本均值和样本标准差：选择要用于估计总体参数的样本统计信息，如样本均值、样本标准差。总体参数是一个表示特定总体特性的值；
   4. 选择所需的置信度：最常用的置信度是90%、95%和99%；
   5. 计算误差范围：可以使用以下公式计算误差裕度： Z_(a/2) * σ/√(n). Z_(a/2) = 置信度系数，其中A=置信度，σ=标准差，N=样本量。这个公式的意义是用标准误差乘以临界值。下面将此公式分解为多个部分来进行求解：
      1. 找到临界值Za/2：假设置信水平95%，则显著水平α等于0.05， 则上分位点右侧的概率值为0.025，注意查z值表时z（0.025）的数值对应的概率值为1-0.025=0.975，即表示该分位点左侧的概率值：

         

         根据对应概率值查找相应分位点值，若表格中无此概率值，则取较接近的概率值即可。恰好表格中有0.975，该数据行最左侧数值为1.9，数据所在列最上端数据为0.06，则Z（0.025）=1.96，即行头表示前两位数字，列头表示末尾数字。
      2. 找到标准误差：假设标准偏差x，再除以样本大小的平方根
      3. 将临界值乘以标准误差得到误差幅度；
   6.  说明置信区间：
      1. 只需取平均值，并将其写在±和误差裕度旁边。可以通过从均值中加上和减去误差，找到置信区间的上下限；
      2. 也可以使用这个公式来查找置信区间： x̅ ± Z_(a/2) * σ/√(n) 。x̅表示平均值。
3. some tips
   1. 样本总体必须是正态的，置信区间才有效。
   2. 用于计算误差幅度的临界值是一个常数，表示为T分值或Z分值。当总体标准偏差未知或使用小样本时，T分数通常是首选的。
   3. 有许多方法可以抽取样本，如简单随机抽样、系统抽样和分层抽样。你可以从中选择一个有代表性的样本来检验你的假设。
   4. 置信区间不表示特定结果的概率。例如，如果你95%确信你的人口平均值在75到100之间，95%的置信区间并不意味着平均值落入你计算范围内的概率为95%。