一、pcl中点云配准算法

PCL 库中 ICP 的接口及其变种：

点到点：pcl::IterativeClosestPoint< PointSource, PointTarget, Scalar >
点到面：pcl::IterativeClosestPointWithNormals< PointSource, PointTarget, Scalar >
面到面：pcl::GeneralizedIterativeClosestPoint< PointSource, PointTarget >

其中，IterativeClosestPoint 模板类是 ICP 算法的一个基本实现，其优化求解方法基于 Singular Value Decomposition (SVD)，算法迭代结束条件包括：

最大迭代次数：Number of iterations has reached the maximum user imposed number of iterations (via setMaximumIterations)
两次变换矩阵之间的差值：The epsilon (difference) between the previous transformation and the current estimated transformation is smaller than an user imposed value (via setTransformationEpsilon)
均方误差：The sum of Euclidean squared errors is smaller than a user defined threshold (via setEuclideanFitnessEpsilon)

基本用法：

IterativeClosestPoint<PointXYZ, PointXYZ> icp;

// Set the input source and target
icp.setInputCloud (cloud_source);
icp.setInputTarget (cloud_target);

// Set the max correspondence distance to 5cm (e.g., correspondences with higher distances will be ignored)
icp.setMaxCorrespondenceDistance (0.05);
// Set the maximum number of iterations (criterion 1)
icp.setMaximumIterations (50);
// Set the transformation epsilon (criterion 2)
icp.setTransformationEpsilon (1e-8);
// Set the euclidean distance difference epsilon (criterion 3)
icp.setEuclideanFitnessEpsilon (1);

// Perform the alignment
icp.align (cloud_source_registered);
// Obtain the transformation that aligned cloud_source to cloud_source_registered
Eigen::Matrix4f transformation = icp.getFinalTransformation ();

两帧点云配置算法可以看这里

How to incrementally register pairs of clouds — Point Cloud Library 0.0 documentation (pcl.readthedocs.io)

GitHub - geekerboy/pairwise_incremental_registration: 修复参考书代码中Segmentation fault (core dumped) 问题

二、关于svd原理求解部分

高翔视觉SLAM十四讲求解 ICP 的代码

void pose_estimation_3d3d(const vector<Point3f>& pts1,
                          const vector<Point3f>& pts2,
                          Mat& R, Mat& t)
{
    // 求质心
    Point3f p1, p2;
    int N = pts1.size();
    for (int i=0; i<N; i++)
    {
        p1 += pts1[i];
        p2 += pts2[i];
    }
    p1 /= N;
    p2 /= N;

    // 去质心
    vector<Point3f> q1(N), q2(N);
    for (int i=0; i<N; i++)
    {
        q1[i] = pts1[i] - p1;
        q2[i] = pts2[i] - p2;
    }

    // 计算 q1*q2^T
    Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
    for (int i=0; i<N; i++)
    {
        W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x,
                q2[i].y, q2[i].z).transpose();
    }
    cout << "W=" << W << endl;

    // 对W进行SVD求解Rt
    Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();
    cout << "U=" << U << endl;
    cout << "V=" << V << endl;

    Eigen::Matrix3d R_ = U * (V.transpose());
    Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);

    // Eigen 转换成 cv::Mat
    R = (Mat_<double>(3, 3) <<
            R_(0, 0), R_(0, 1), R_(0,2),
            R_(1, 0), R_(1, 1), R_(1,2),
            R_(2, 0), R_(2, 1), R_(2,2));
    t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}

另外的方法求RT，本质也是svd分解

/// <summary>
/// 通过svd分解求解旋转和平移
/// </summary>
/// <param name="A"></param>
/// <param name="B"></param>
/// <returns>返回值为4*4变换矩阵T</returns>
Eigen::Matrix4d best_fit_transform(const Eigen::MatrixXd& A, const Eigen::MatrixXd& B) {
    /*
    Notice:
    1/ JacobiSVD return U,S,V, S as a vector, "use U*S*Vt" to get original Matrix;
    2/ matrix type 'MatrixXd' or 'MatrixXf' matters.
    */
    Eigen::Matrix4d T = Eigen::MatrixXd::Identity(4, 4);
    Eigen::Vector3d centroid_A(0, 0, 0);
    Eigen::Vector3d centroid_B(0, 0, 0);
    Eigen::MatrixXd AA = A;
    Eigen::MatrixXd BB = B;
    int row = A.rows();

    for (int i = 0; i < row; i++) {
        centroid_A += A.block<1, 3>(i, 0).transpose();
        centroid_B += B.block<1, 3>(i, 0).transpose();
    }
    centroid_A /= row;
    centroid_B /= row;
    for (int i = 0; i < row; i++) {
        AA.block<1, 3>(i, 0) = A.block<1, 3>(i, 0) - centroid_A.transpose();
        BB.block<1, 3>(i, 0) = B.block<1, 3>(i, 0) - centroid_B.transpose();
    }

    Eigen::MatrixXd H = AA.transpose() * BB;
    Eigen::MatrixXd U;
    Eigen::VectorXd S;
    Eigen::MatrixXd V;
    Eigen::MatrixXd Vt;
    Eigen::Matrix3d R;
    Eigen::Vector3d t;

    JacobiSVD<Eigen::MatrixXd> svd(H, ComputeFullU | ComputeFullV);
    U = svd.matrixU();
    S = svd.singularValues();
    V = svd.matrixV();
    Vt = V.transpose();
    R = Vt.transpose() * U.transpose();

    if (R.determinant() < 0) {
        Vt.block<1, 3>(2, 0) *= -1;
        R = Vt.transpose() * U.transpose();
    }

    t = centroid_B - R * centroid_A;

    T.block<3, 3>(0, 0) = R;
    T.block<3, 1>(0, 3) = t;
    return T;

}

icp求解是利用pcl工具来做，省时省力。

Introduction — Point Cloud Library 1.12.1-dev documentation (pointclouds.org)

Interactive Iterative Closest Point — Point Cloud Library 1.12.1-dev documentation (pointclouds.org)

三、pcl IterativeClosestPoint 完成demo

代码：

#include <iostream>
#include <numeric>
#include "icp.h"
#include "Eigen/Eigen"

using namespace std;
using namespace Eigen;


/// <summary>
/// 通过svd分解求解旋转和平移
/// </summary>
/// <param name="A"></param>
/// <param name="B"></param>
/// <returns>返回值为4*4变换矩阵T</returns>
Eigen::Matrix4d best_fit_transform(const Eigen::MatrixXd& A, const Eigen::MatrixXd& B) {
    /*
    Notice:
    1/ JacobiSVD return U,S,V, S as a vector, "use U*S*Vt" to get original Matrix;
    2/ matrix type 'MatrixXd' or 'MatrixXf' matters.
    */
    Eigen::Matrix4d T = Eigen::MatrixXd::Identity(4, 4);
    Eigen::Vector3d centroid_A(0, 0, 0);
    Eigen::Vector3d centroid_B(0, 0, 0);
    Eigen::MatrixXd AA = A;
    Eigen::MatrixXd BB = B;
    int row = A.rows();

    for (int i = 0; i < row; i++) {
        centroid_A += A.block<1, 3>(i, 0).transpose();
        centroid_B += B.block<1, 3>(i, 0).transpose();
    }
    centroid_A /= row;
    centroid_B /= row;
    for (int i = 0; i < row; i++) {
        AA.block<1, 3>(i, 0) = A.block<1, 3>(i, 0) - centroid_A.transpose();
        BB.block<1, 3>(i, 0) = B.block<1, 3>(i, 0) - centroid_B.transpose();
    }

    Eigen::MatrixXd H = AA.transpose() * BB;
    Eigen::MatrixXd U;
    Eigen::VectorXd S;
    Eigen::MatrixXd V;
    Eigen::MatrixXd Vt;
    Eigen::Matrix3d R;
    Eigen::Vector3d t;

    JacobiSVD<Eigen::MatrixXd> svd(H, ComputeFullU | ComputeFullV);
    U = svd.matrixU();
    S = svd.singularValues();
    V = svd.matrixV();
    Vt = V.transpose();
    R = Vt.transpose() * U.transpose();

    if (R.determinant() < 0) {
        Vt.block<1, 3>(2, 0) *= -1;
        R = Vt.transpose() * U.transpose();
    }

    t = centroid_B - R * centroid_A;

    T.block<3, 3>(0, 0) = R;
    T.block<3, 1>(0, 3) = t;
    return T;

}

/*
typedef struct{
    Eigen::Matrix4d trans;
    std::vector<float> distances;
    int iter;
}  ICP_OUT;
*/

ICP_OUT icp(const Eigen::MatrixXd& A, const Eigen::MatrixXd& B, int max_iterations, int tolerance) {
    int row = A.rows();
    Eigen::MatrixXd src = Eigen::MatrixXd::Ones(3 + 1, row);
    Eigen::MatrixXd src3d = Eigen::MatrixXd::Ones(3, row);
    Eigen::MatrixXd dst = Eigen::MatrixXd::Ones(3 + 1, row);
    NEIGHBOR neighbor;
    Eigen::Matrix4d T;
    Eigen::MatrixXd dst_chorder = Eigen::MatrixXd::Ones(3, row);
    ICP_OUT result;
    int iter = 0;

    for (int i = 0; i < row; i++) {
        src.block<3, 1>(0, i) = A.block<1, 3>(i, 0).transpose();
        src3d.block<3, 1>(0, i) = A.block<1, 3>(i, 0).transpose();
        dst.block<3, 1>(0, i) = B.block<1, 3>(i, 0).transpose();
    }

    double prev_error = 0;
    double mean_error = 0;
    for (int i = 0; i < max_iterations; i++) 
    {
        neighbor = nearest_neighbot(src3d.transpose(), B);
        for (int j = 0; j < row; j++) 
        {
            dst_chorder.block<3, 1>(0, j) = dst.block<3, 1>(0, neighbor.indices[j]);
        }
        T = best_fit_transform(src3d.transpose(), dst_chorder.transpose());
        src = T * src;
        for (int j = 0; j < row; j++) 
        {
            src3d.block<3, 1>(0, j) = src.block<3, 1>(0, j);
        }
        mean_error = std::accumulate(neighbor.distances.begin(), neighbor.distances.end(), 0.0) / neighbor.distances.size();
        if (abs(prev_error - mean_error) < tolerance) 
        {
            break;
        }
        prev_error = mean_error;
        iter = i + 2;
    }

    T = best_fit_transform(A, src3d.transpose());
    result.trans = T;
    result.distances = neighbor.distances;
    result.iter = iter;

    return result;
}

/*
typedef struct{
    std::vector<float> distances;
    std::vector<int> indices;
} NEIGHBOR;
*/

NEIGHBOR nearest_neighbot(const Eigen::MatrixXd& src, const Eigen::MatrixXd& dst) {
    int row_src = src.rows();
    int row_dst = dst.rows();
    Eigen::Vector3d vec_src;
    Eigen::Vector3d vec_dst;
    NEIGHBOR neigh;
    float min = 100;
    int index = 0;
    float dist_temp = 0;

    for (int ii = 0; ii < row_src; ii++) {
        vec_src = src.block<1, 3>(ii, 0).transpose();
        min = 100;
        index = 0;
        dist_temp = 0;
        for (int jj = 0; jj < row_dst; jj++) {
            vec_dst = dst.block<1, 3>(jj, 0).transpose();
            dist_temp = dist(vec_src, vec_dst);
            if (dist_temp < min) {
                min = dist_temp;
                index = jj;
            }
        }
        // cout << min << " " << index << endl;
        // neigh.distances[ii] = min;
        // neigh.indices[ii] = index;
        neigh.distances.push_back(min);
        neigh.indices.push_back(index);
    }

    return neigh;
}


float dist(const Eigen::Vector3d& pta, const Eigen::Vector3d& ptb) {
    return sqrt((pta[0] - ptb[0]) * (pta[0] - ptb[0]) + (pta[1] - ptb[1]) * (pta[1] - ptb[1]) + (pta[2] - ptb[2]) * (pta[2] - ptb[2]));
}

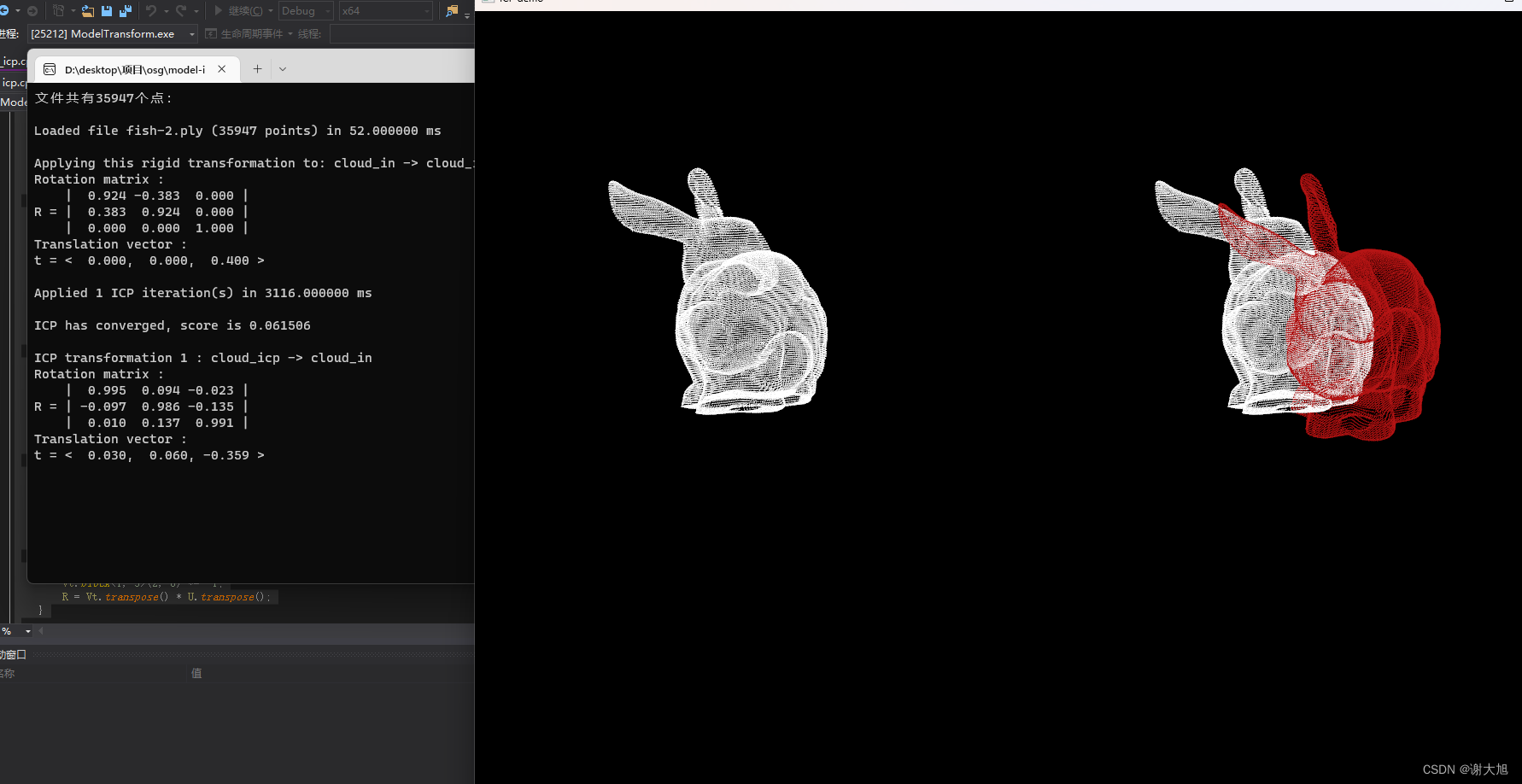
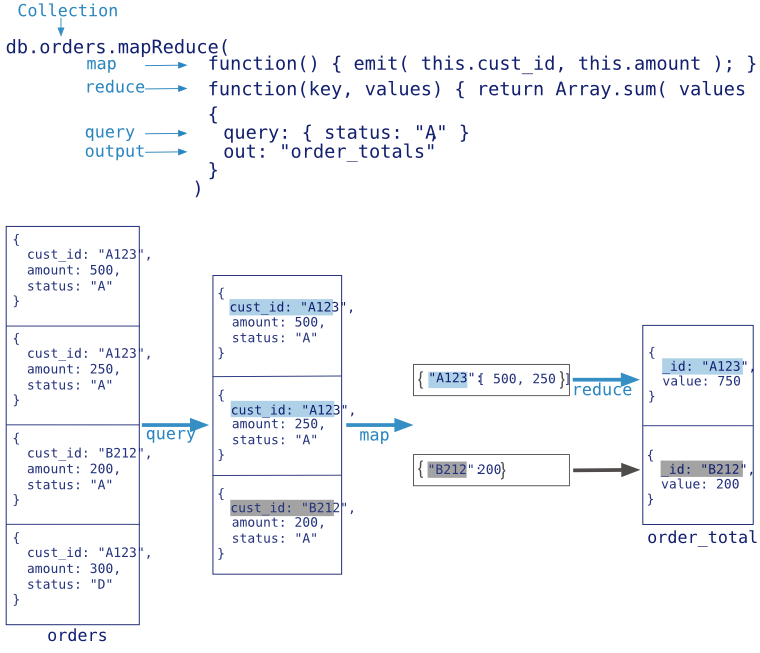
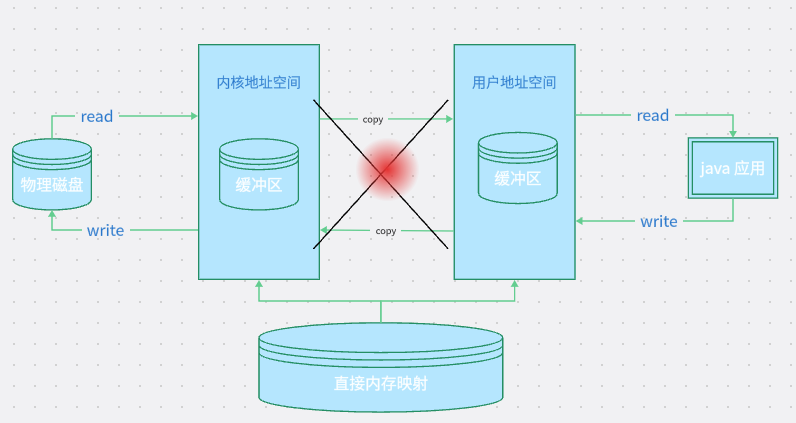
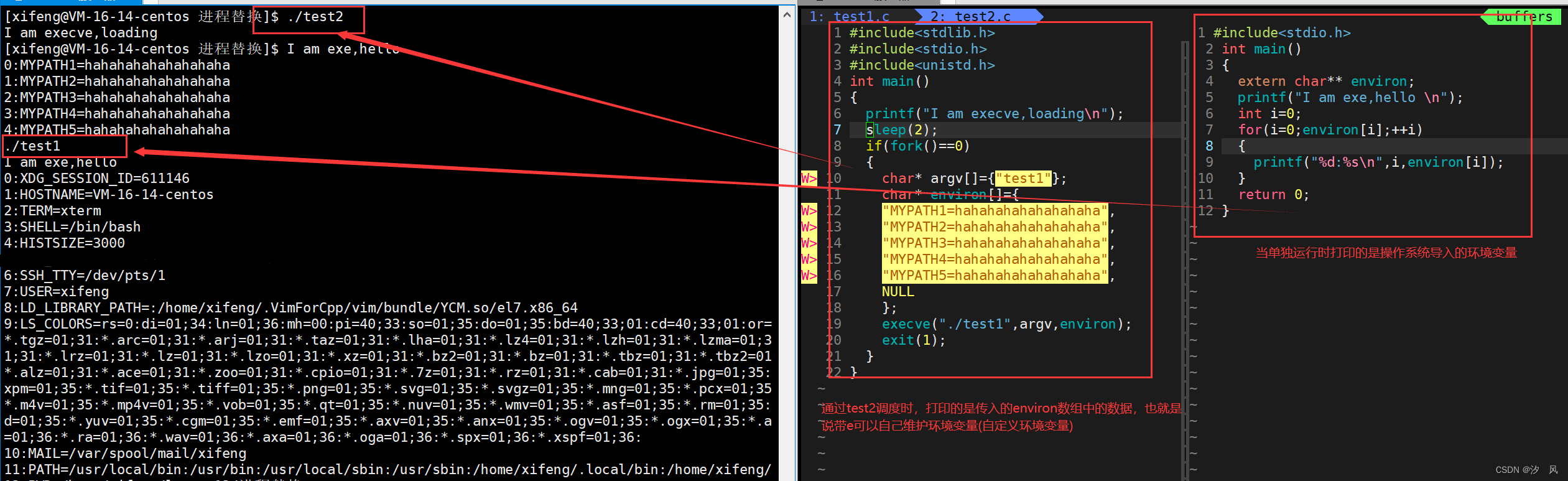
截图：