文章目录
- 1. 图的遍历
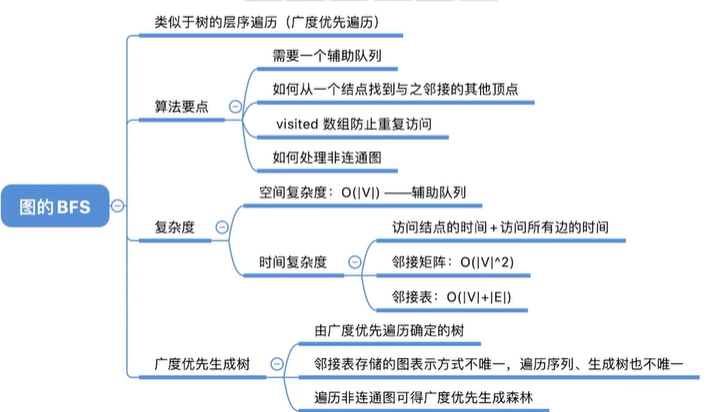
- 1.1 广度优先搜索(BFS)
- 1.1.1 遍历序列的可变性
- 1.1.2 复杂度的分析
- 1.1.3 广度优先生成树
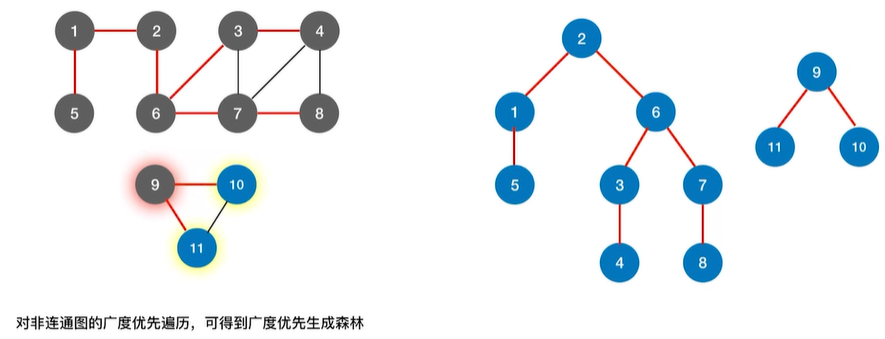
- 1..1.4 广度优先生成森林
- 1.2 深度优先搜索(DFS)
- 1.2.1 树的深度优先遍历
- 1.2.2 图的深度优先遍历
- 1.2.2 复杂度的分析
- 1.2.4 深度优先遍历序列
- 1.2.5 深度优先生成树
- 1.3 图的遍历与图的连通性·
- 总结
- 2. 图的应用
- 2.1 最小生成树
- 2.1.1 最小生成树的概念
- 2.1.2 Prim算法
- 2.1.3 Kruskal算法
- 2.2 最短路径(BFS算法——无权值)
- 2.2.1 BFS求无权图的单源最短路径
- 2.2.2 最短路径——Dijkstra(迪杰斯特拉)算法
- 2.2.2.1 BFS算法的局限性
- 2.2.2.2 Dijkstra算法
- (1). 如何使用数组信息?
- (2)Dijkstra算法的时间复杂度
- (3) 用于负权值带权图
- 2.2.3 最短路径——Floyd(弗洛伊德)算法
- 2.2.3.1 Floyd算法用于负权图
- 2.3 有向无环图(DAG)描述表达式
- 2.3.1 DAG描述表达式
- 2.4 拓扑排序
- 2.4.1 AOV网
- 2.4.2 拓扑排序
- 2.4.3 对有回路的图进行拓扑排序
- 2.4.4 逆拓扑排序
- 2.5 关键路径
- 2.5.1 AOE网
- 2.5.2 关键路径
- 2.5.3 求关键路径的步骤
- 2.5.4 关键活动、关键路径的特性
1. 图的遍历
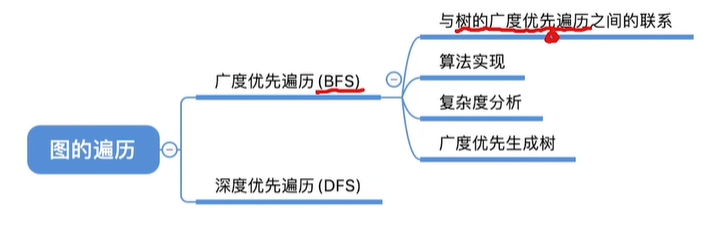
教程:https://www.bilibili.com/video/BV1b7411N798/?p=59&share_source=copy_web&vd_source=d228985826b563972268952905224139)
图的遍历是指从图中的某一顶点出发,按照某种搜索方法沿着图中的边对图中的所有顶点访问一次且仅访问一次。
注意到树是一种特殊的图,所以树的遍历实际上也可视为一种特殊的图的遍历。
图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。
图的遍历比树的遍历要复杂得多,因为图的任一顶点都可能和其余的顶点相邻接,所以在访问某个顶点后,可能沿着某条路径搜索又回到该顶点上。为避免同一顶点被访问多次,在遍历图的过程中,必须记下每个已访问过的顶点,为此可以设一个辅助数组visited []来标记顶点是否被访问过。
图的遍历算法主要有两种:广度优先搜索和深度优先搜索。
1.1 广度优先搜索(BFS)
教程:广度优先遍历https://www.bilibili.com/video/BV1b7411N798/?p=59&share_source=copy_web&vd_source=d228985826b563972268952905224139
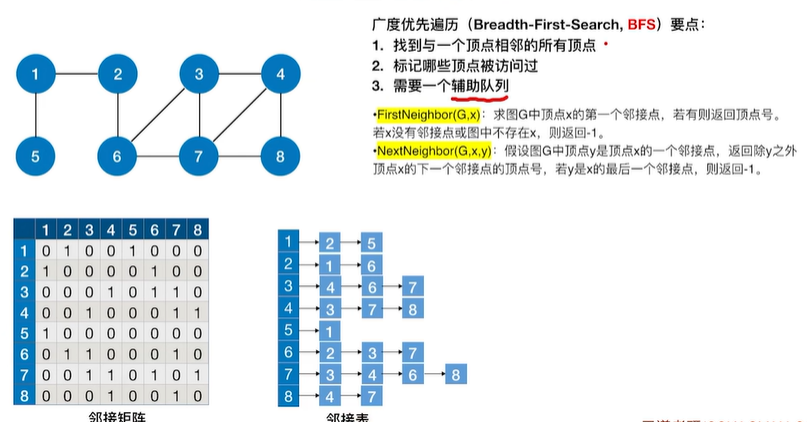
广度优先搜索算法的伪代码如下:
bool visited[MAX_VERTEX_NUM];//访问标记数组
void BFSTraverse(Graph G) { //对图G进行广度优先遍历
for (i = 0; i < G.vexnum; ++i)
visited[i] = FALSE; //访问标记数组初始化
initQueue(Q);//初始化辅助队列Q
for (i = 0; i < G.vexnum; ++i)//从0号顶点开始遍历
if (!visited[i])//对每一个连通分量调用一次BFS
BFS(G, i);//vi未访问过,从vi开始BFS
}
void BFS(Graph G, int v) { //从顶点v出发,广度优先遍历图G
visit(v);//访问初始顶点v
visited[v] = TRUE;//对v做已访问标记
Enqueue(Q, v);//顶点v入队列Q
while (!isEmpty(Q)) {
DeQueue(Q, v); //顶点v出队列
for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))//检测v所有临界点
if (!visited[w]) { //w为v的尚未访问的邻接顶点
visit(w);//访问顶点w
visited[w] = TRUE;//对w做已访问标记
EnQueue(Q, w);//顶点w入队列
}//if
}//while

1.1.1 遍历序列的可变性
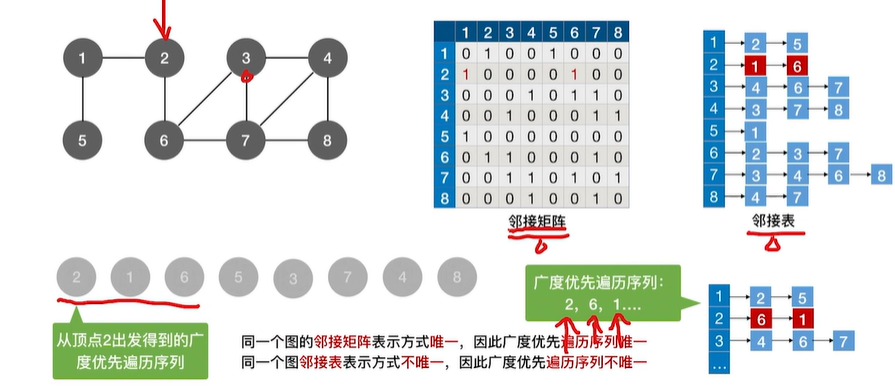
1.1.2 复杂度的分析
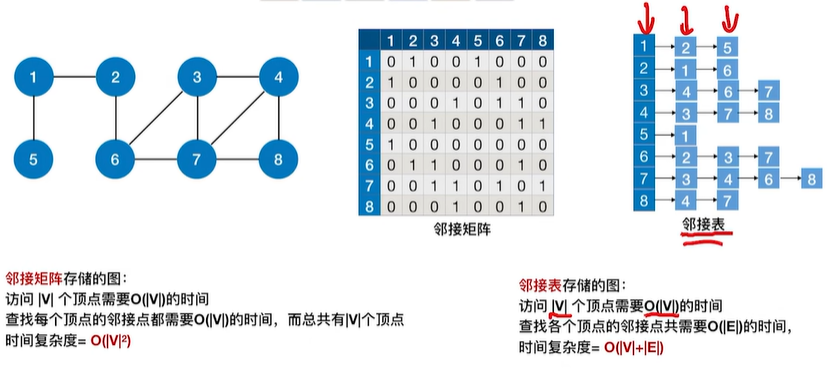


1.1.3 广度优先生成树

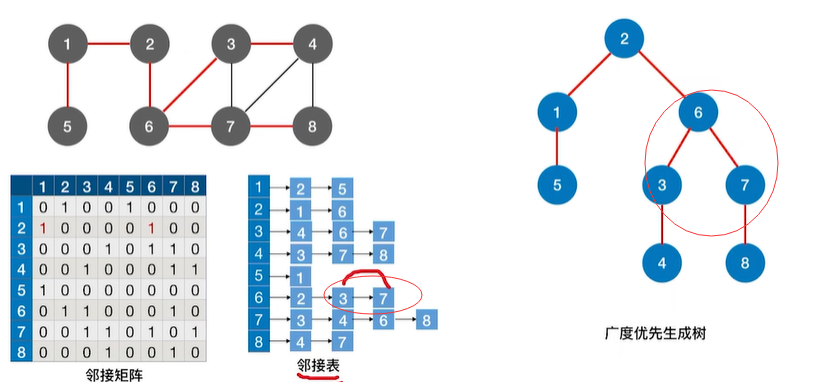
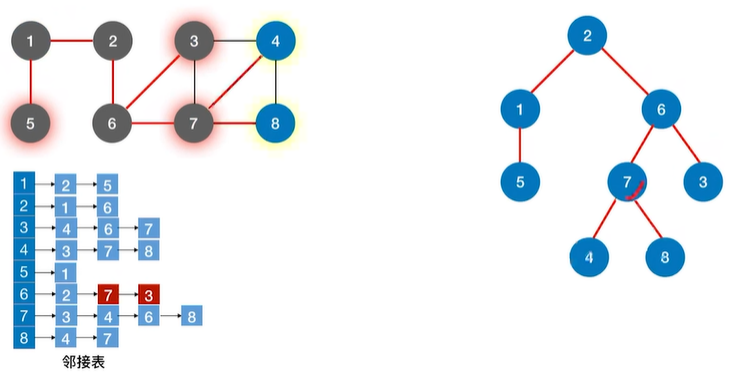
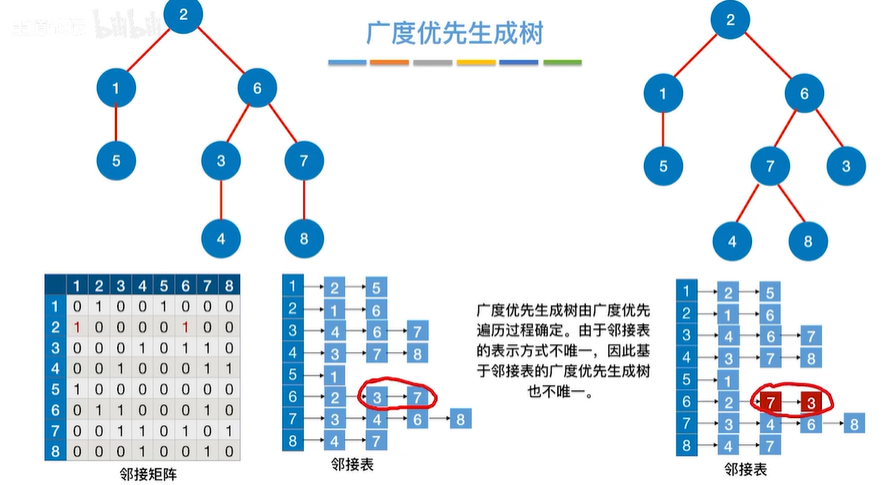
1…1.4 广度优先生成森林
1.2 深度优先搜索(DFS)
教程:深度优先搜索(DFS)https://www.bilibili.com/video/BV1b7411N798/?p=60&share_source=copy_web&vd_source=d228985826b563972268952905224139
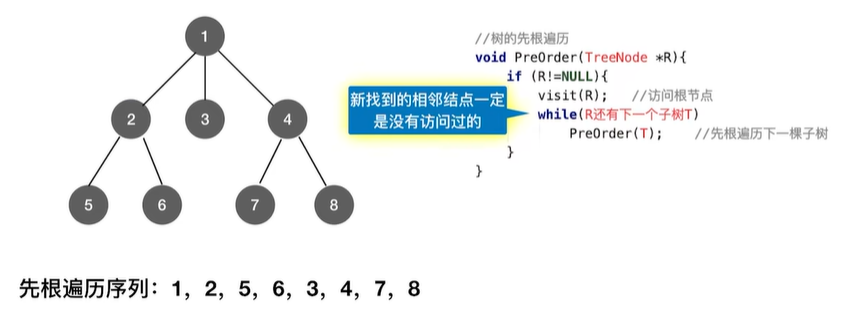
与广度优先搜索不同,深度优先搜索(Depth-First-Search,DFS)类似于树的先序遍历。如其名称中所暗含的意思一样,这种搜索算法所遵循的搜索策略是尽可能“深”地搜索一个图。
它的基本思想如下:首先访问图中某一起始顶点v,然后由v出发,访问与v邻接且未被访问的任一顶点w,再访问与w,邻接且未被访问的任一顶点w……重复上述过程。当不能再继续向下访问时,依次退回到最近被访问的顶点,若它还有邻接顶点未被访问过,则从该点开始继续上述搜索过程,直至图中所有顶点均被访问过为止。
1.2.1 树的深度优先遍历
1.2.2 图的深度优先遍历
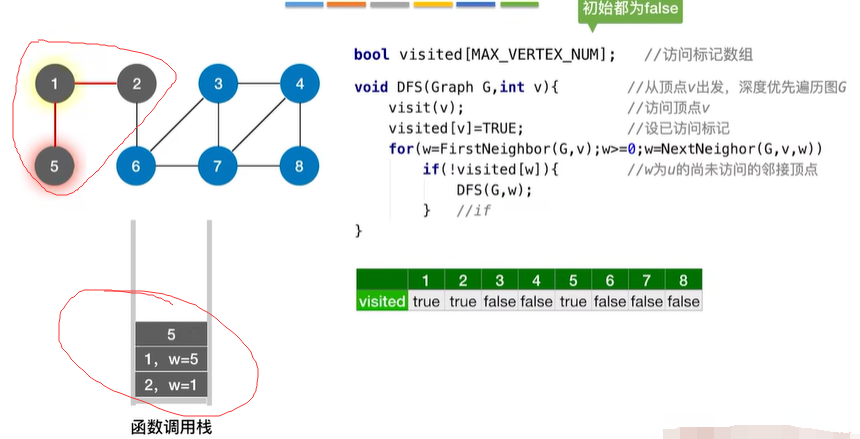
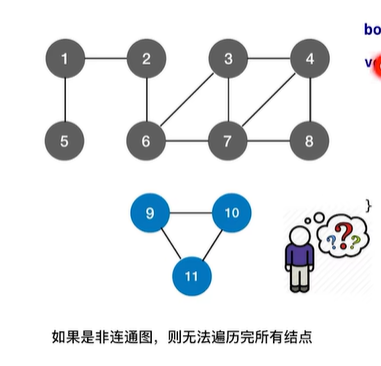
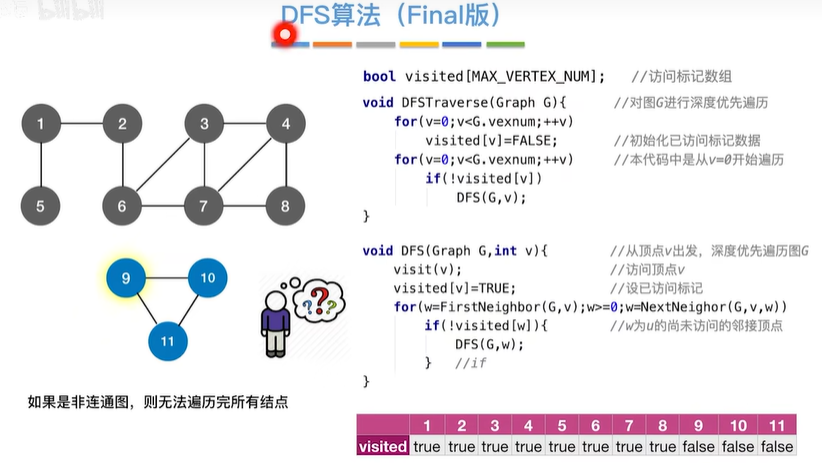
bool visited[MAX_VERTEX_NUM];//访问标记数组
void DFSTraverse(Graph G) { //对图G进行深度优先遍历
for (v= 0; v < G.vexnum; ++v)
visited[v] = FALSE; //访问标记数组初始化
for (v = 0; v < G.vexnum; ++v)//从0号顶点开始遍历
if (!visited[v])//对每一个连通分量调用一次BFS
DFS(G, v);//vi未访问过,从vi开始BFS
}
void DFS(Graph G, int v) { //从顶点v出发,广度优先遍历图G
visit(v);//访问初始顶点v
visited[v] = TRUE;//对v做已访问标记
for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))//检测v所有临界点
if (!visited[w]) { //w为v的尚未访问的邻接顶点
visit(w);//访问顶点w
visited[w] = TRUE;//对w做已访问标记
}//if
}
1.2.2 复杂度的分析
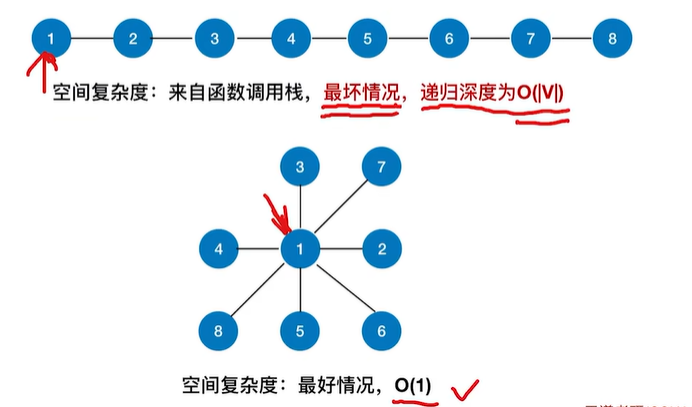
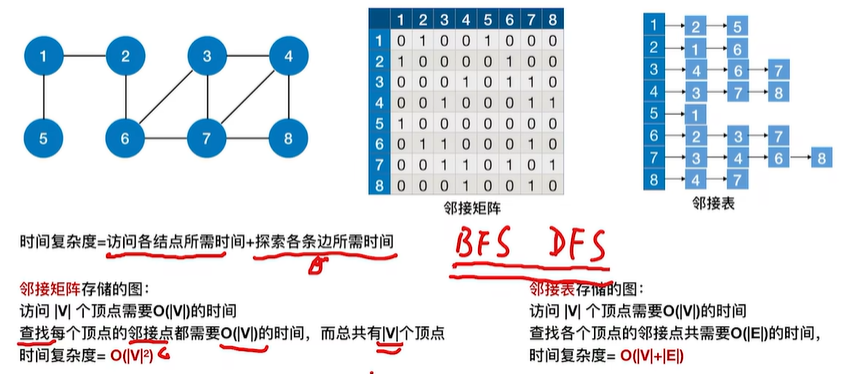
1.2.4 深度优先遍历序列
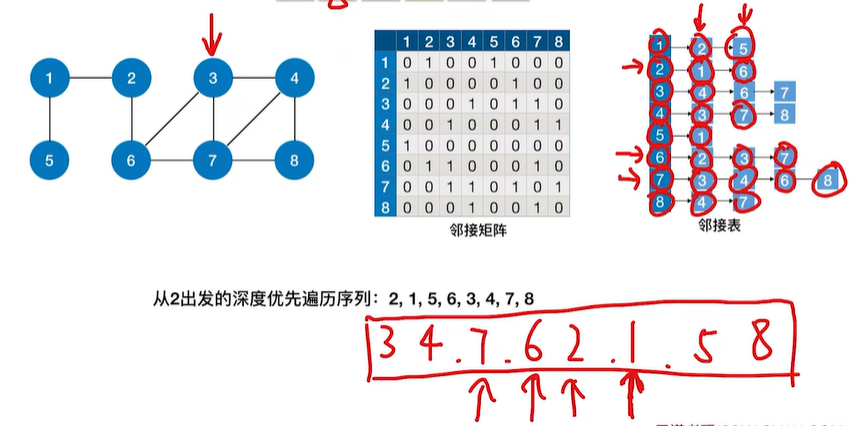

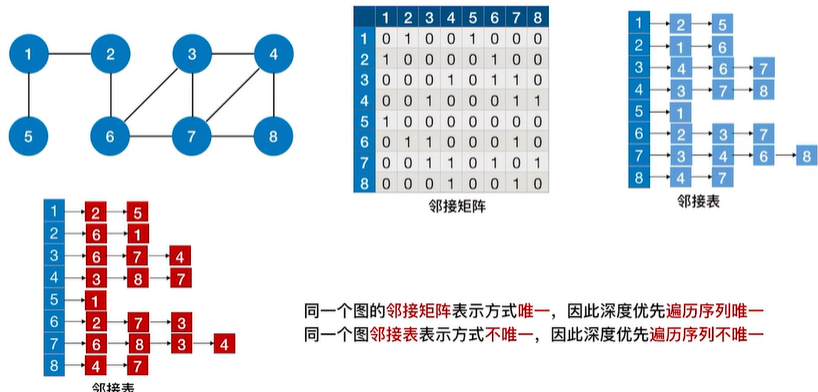
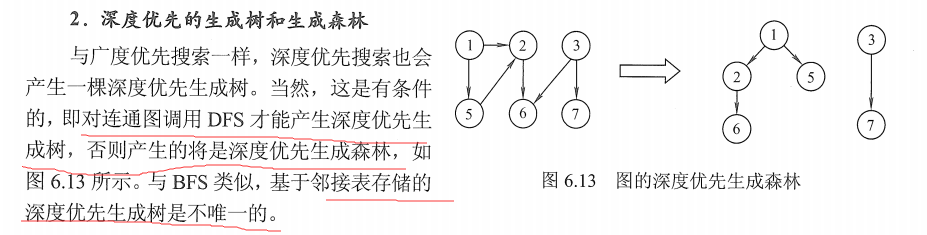
1.2.5 深度优先生成树
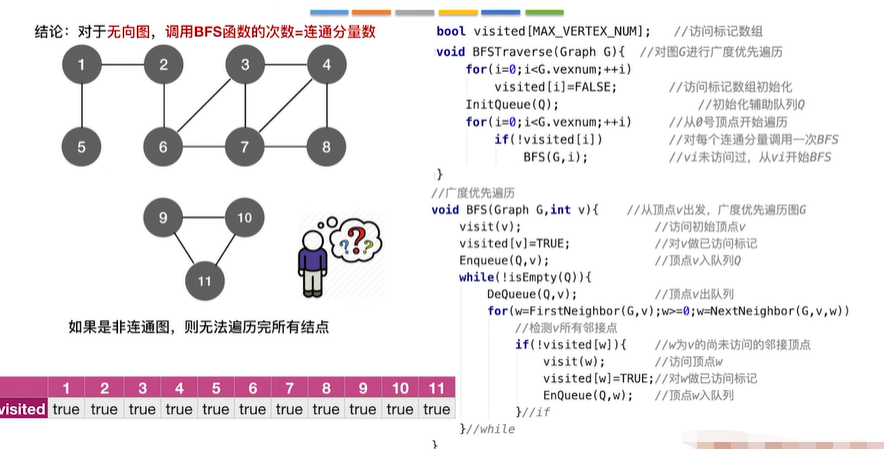
1.3 图的遍历与图的连通性·
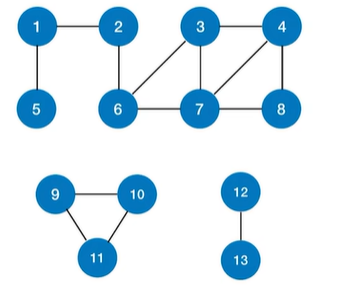
- 对
无向图进行BFS/DFS遍历,调用BFS/DFS函数的次数=连通分量数 - 对于
连通图,只需调用1次BFS/DFS
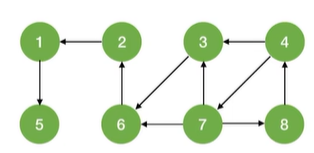
- 对
有向图进行BFS/DFS遍历,调用BFS/DFS函数的次数要具体问题具体分析 - 若起始顶点到其他各顶点都有路径,则只需调用1次BFS/DFS函数
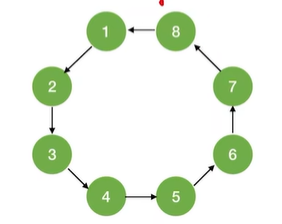
对于强连通图,从任一结点出发都只需调用1次 BFS/DFS
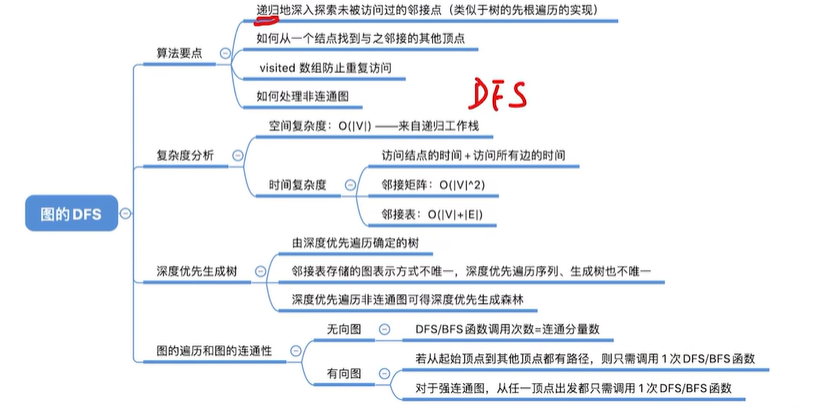
总结
2. 图的应用
2.1 最小生成树
教程:最小生成树 https://www.bilibili.com/video/BV1b7411N798/?p=61&share_source=copy_web&vd_source=d228985826b563972268952905224139
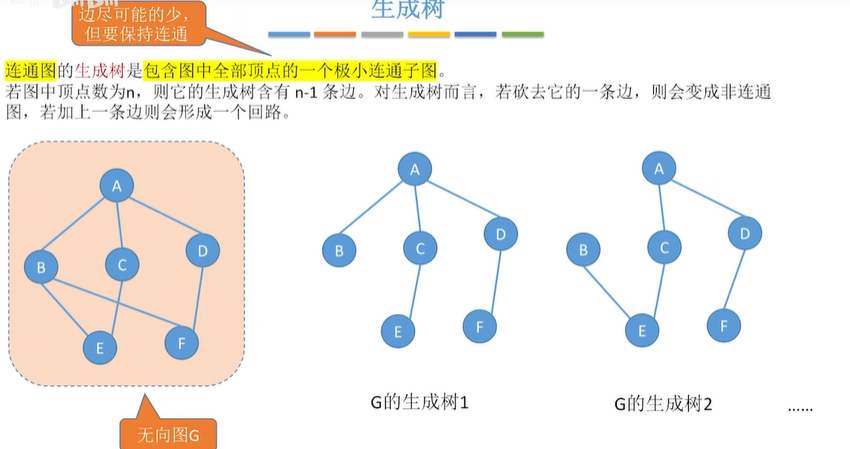
2.1.1 最小生成树的概念
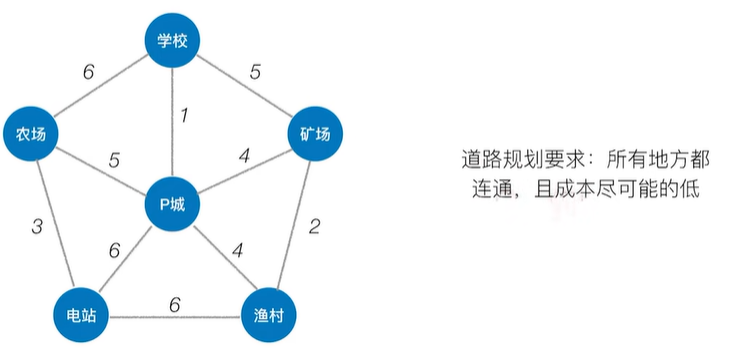
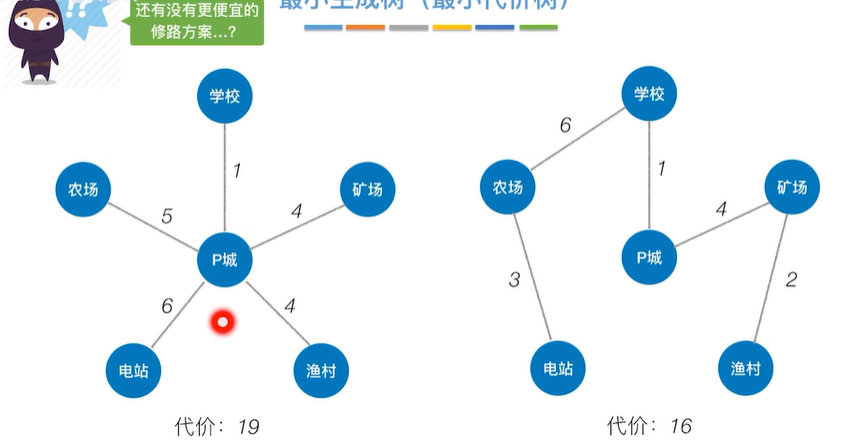

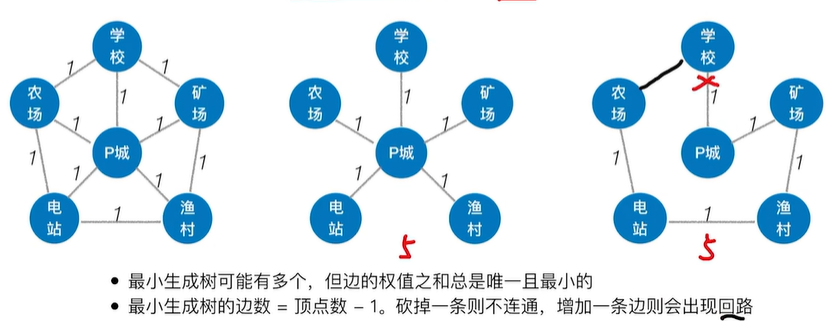
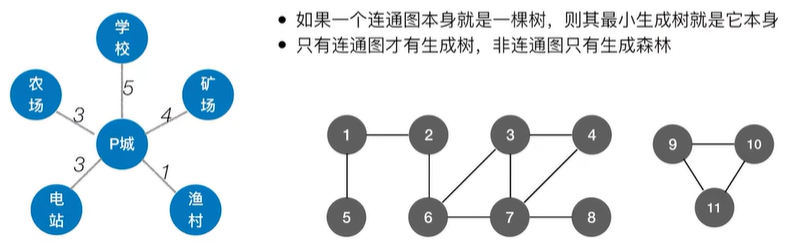
2.1.2 Prim算法
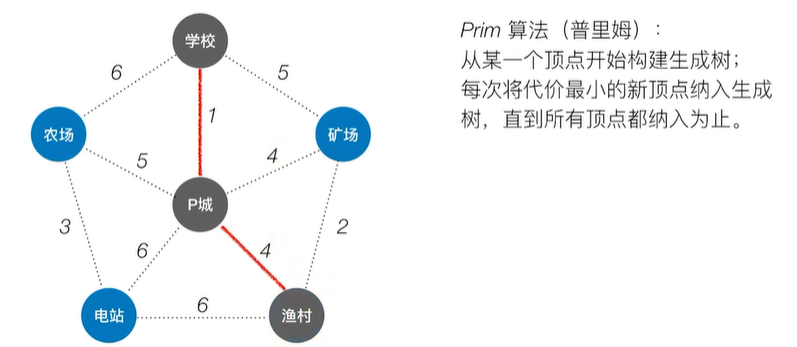

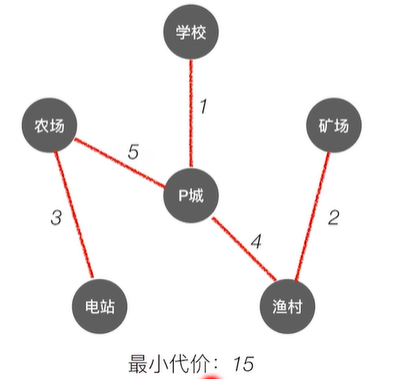
2.1.3 Kruskal算法
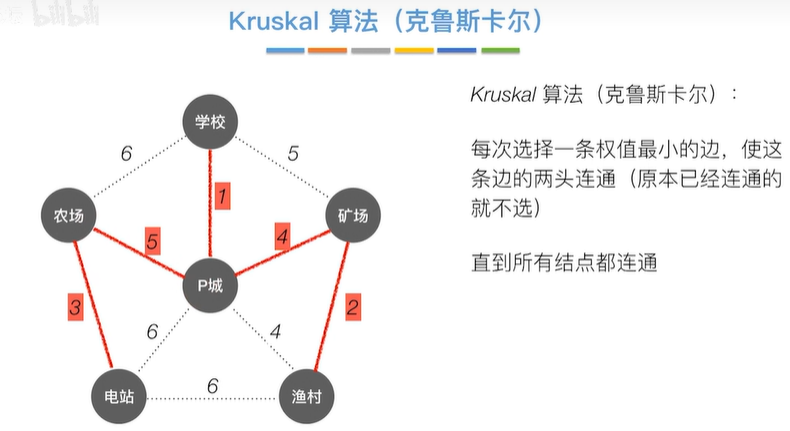

2.2 最短路径(BFS算法——无权值)
教程:最短路径 https://www.bilibili.com/video/BV1b7411N798/?p=62&share_source=copy_web&vd_source=d228985826b563972268952905224139
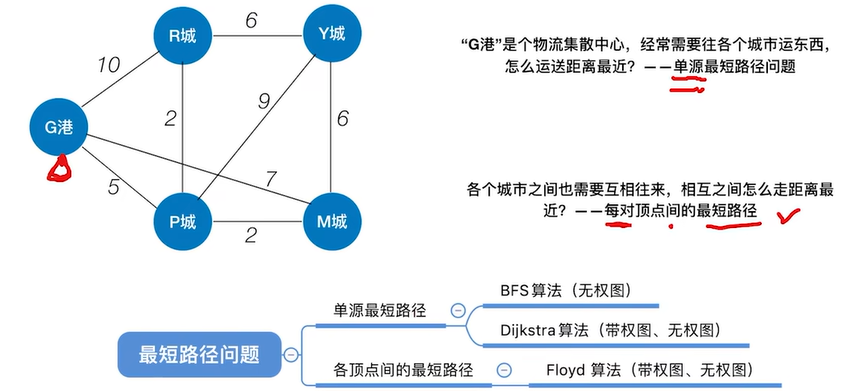
2.2.1 BFS求无权图的单源最短路径
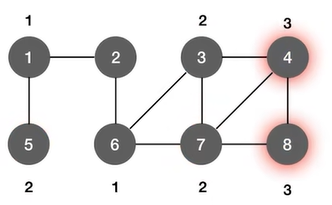
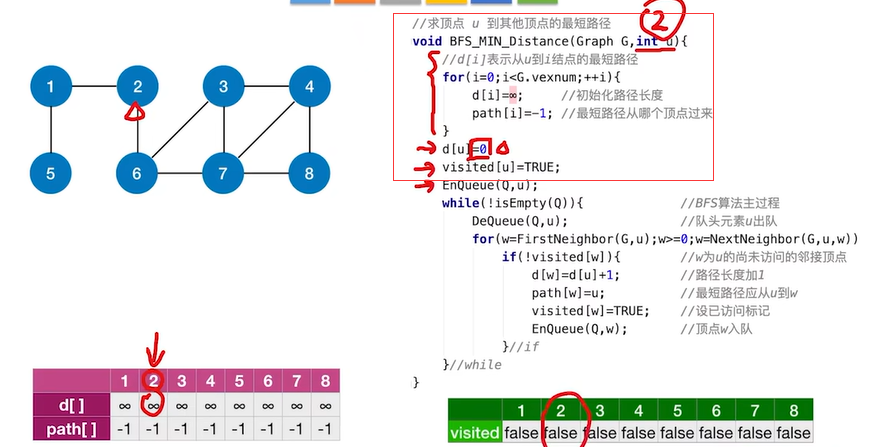
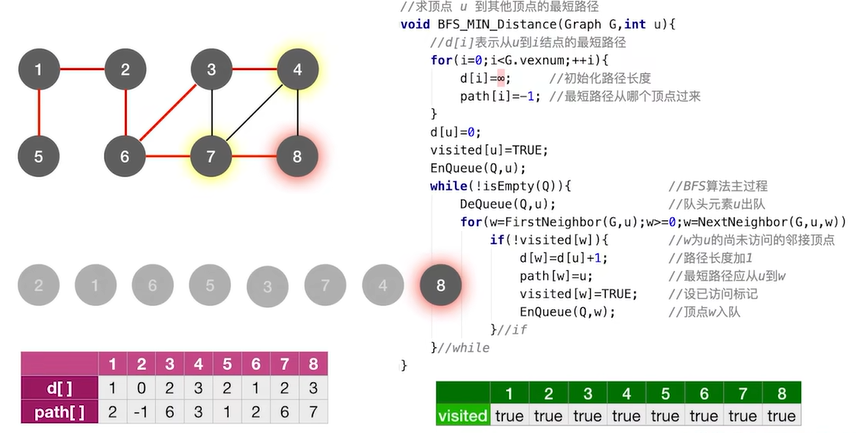
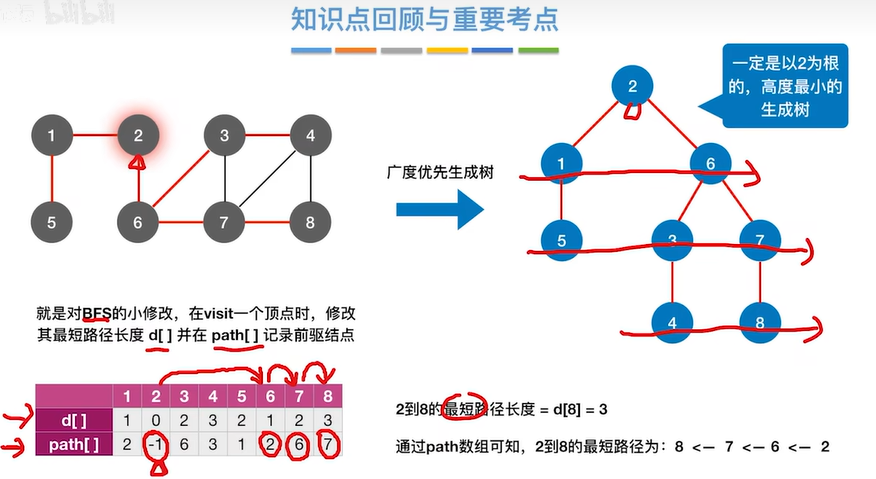
2.2.2 最短路径——Dijkstra(迪杰斯特拉)算法
教程:最短路径——Dijkstra(迪杰斯特拉)算法 https://www.bilibili.com/video/BV1b7411N798/?p=63&share_source=copy_web&vd_source=d228985826b563972268952905224139

2.2.2.1 BFS算法的局限性
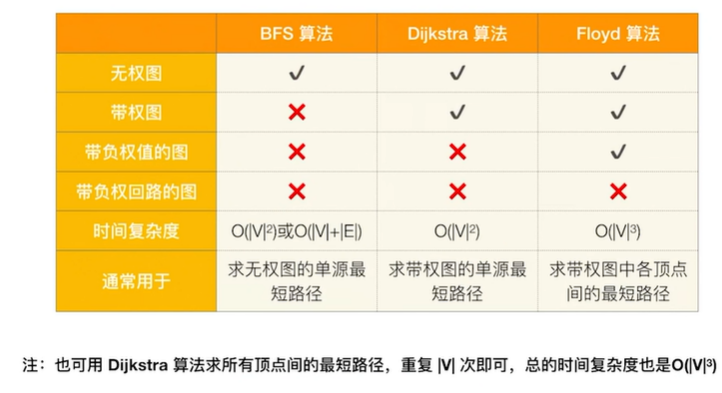
BFS算法求单源最短路径只适用于无权图,或所有边的权值都相同的图

带权路径长度――当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度
2.2.2.2 Dijkstra算法
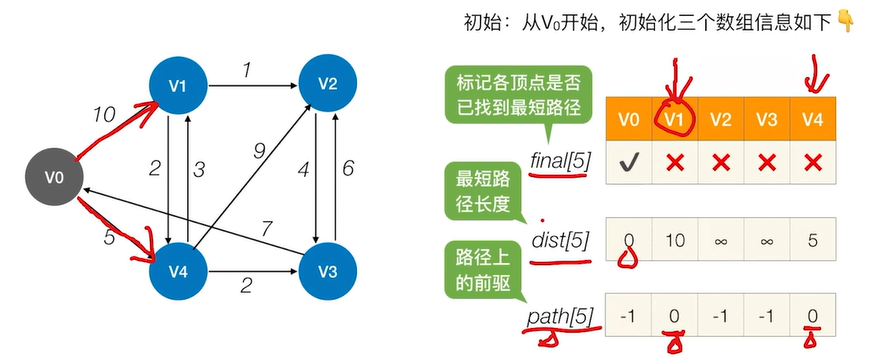
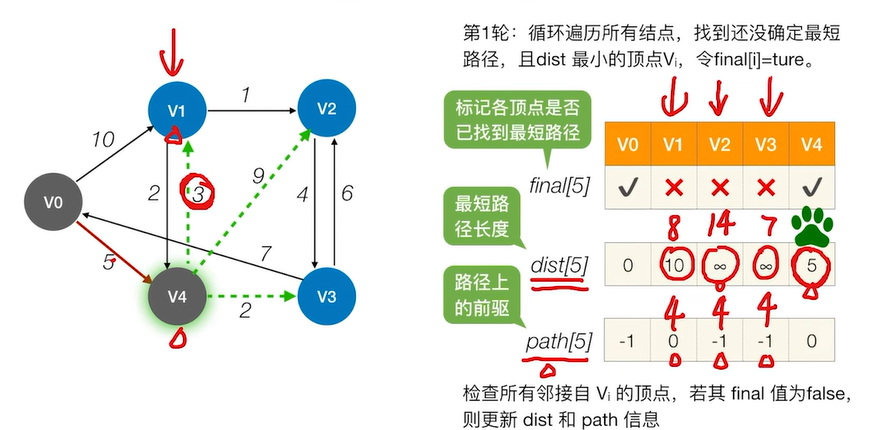
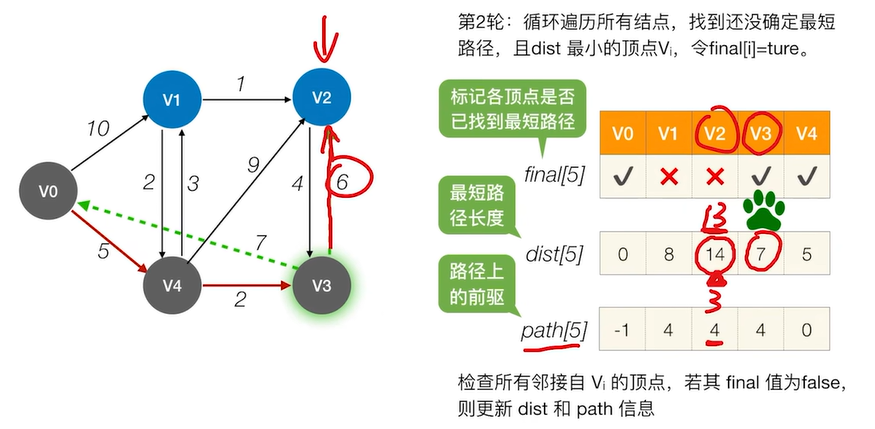
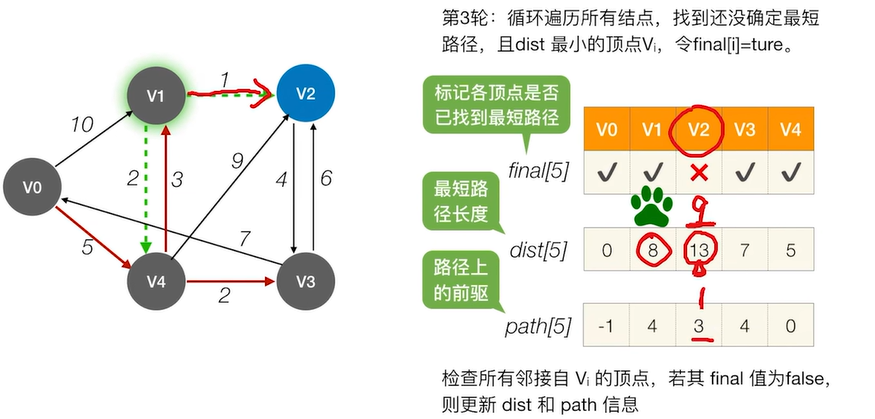
(1). 如何使用数组信息?
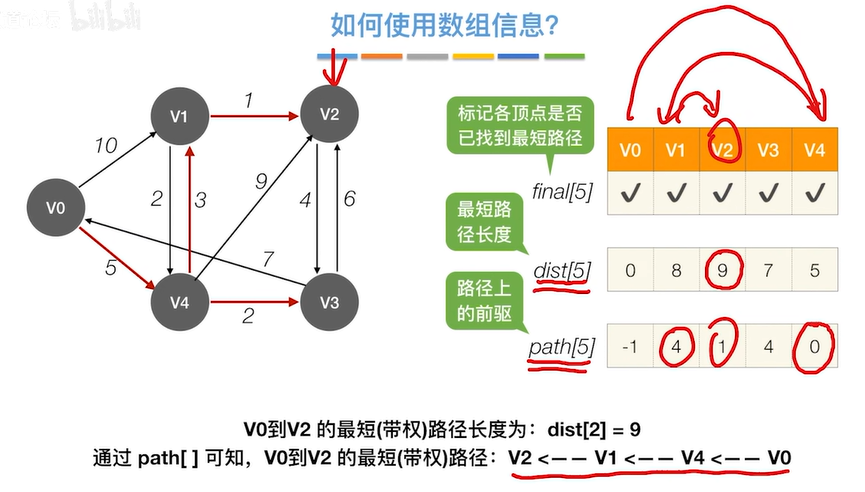
(2)Dijkstra算法的时间复杂度
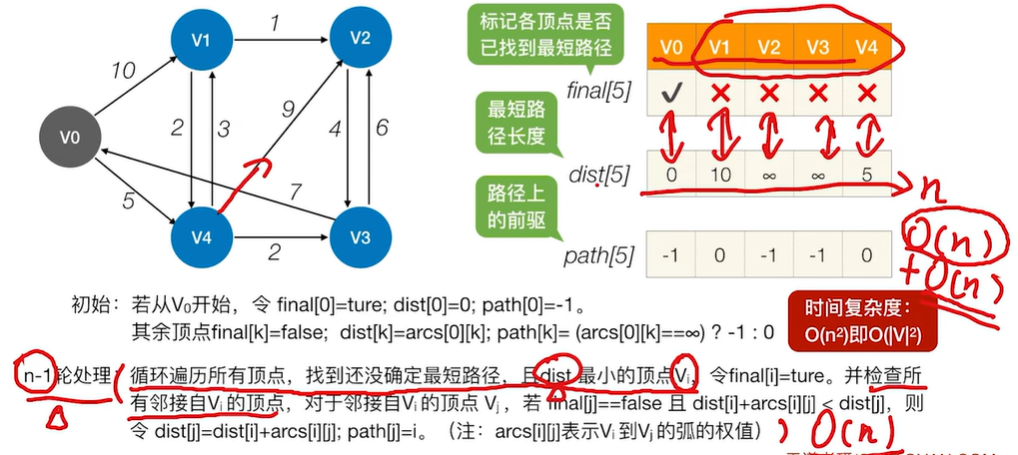
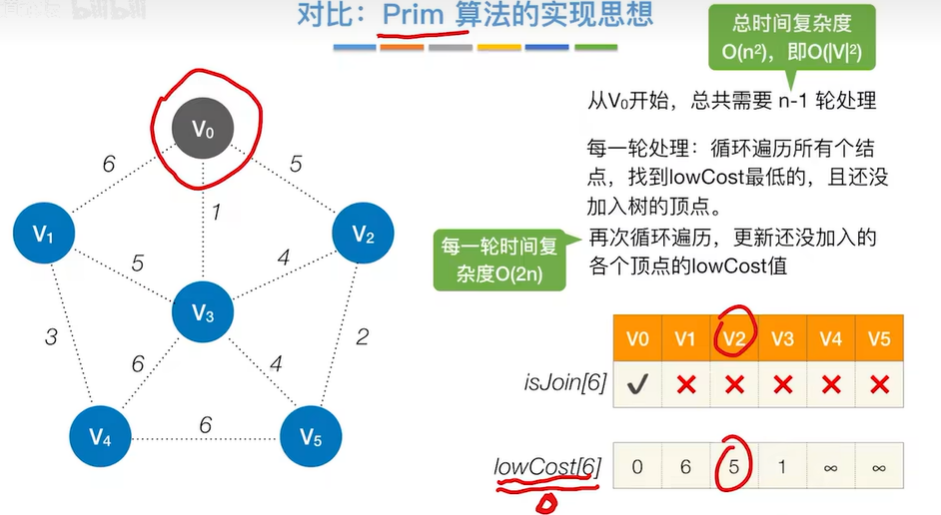
(3) 用于负权值带权图
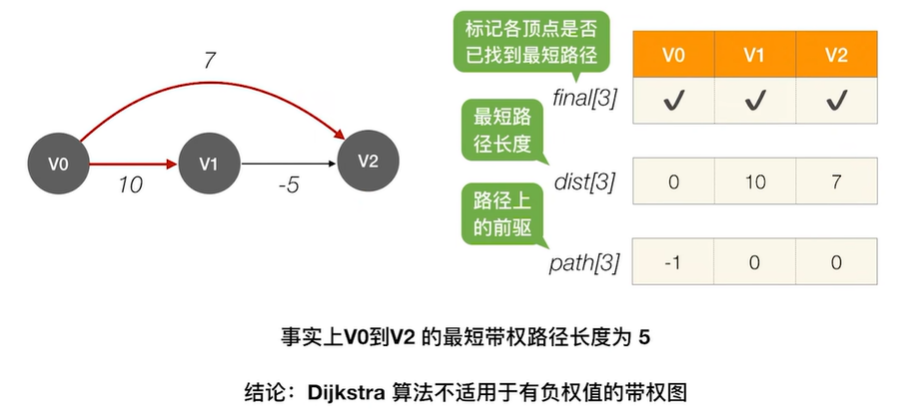
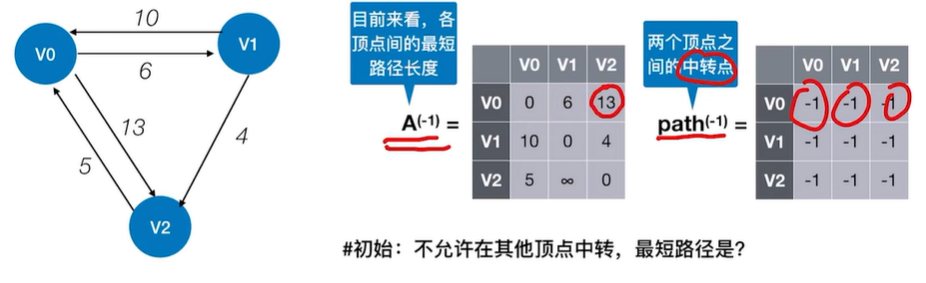
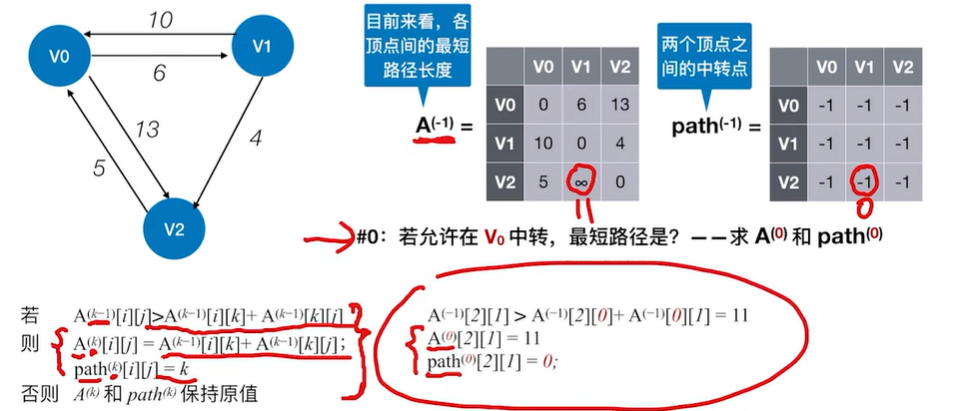
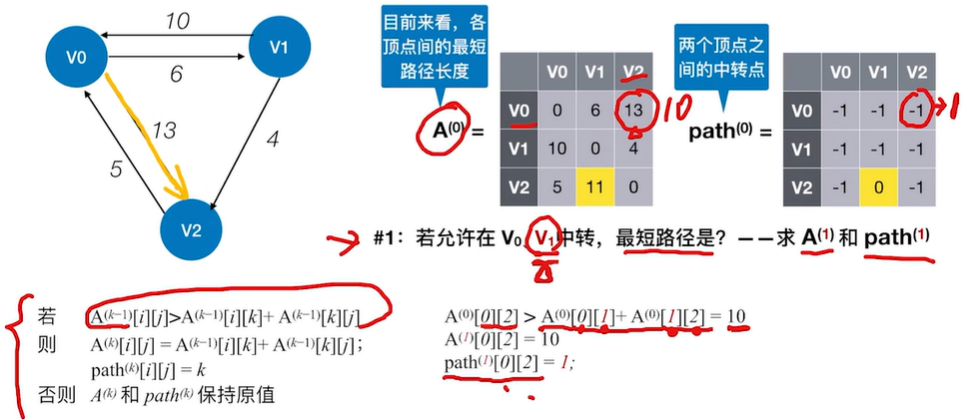
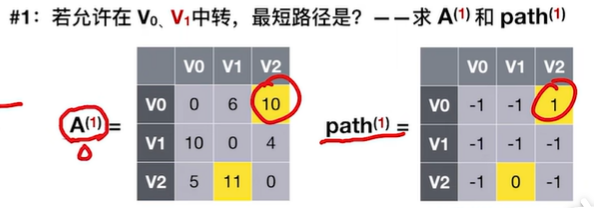
2.2.3 最短路径——Floyd(弗洛伊德)算法
教程:最短路径——Floyd(弗洛伊德)算法: https://www.bilibili.com/video/BV1b7411N798/?p=64&share_source=copy_web&vd_source=d228985826b563972268952905224139


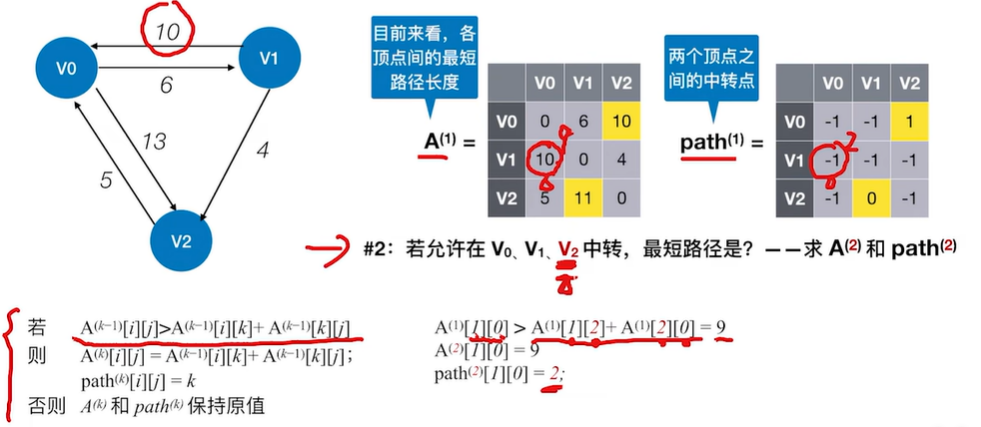
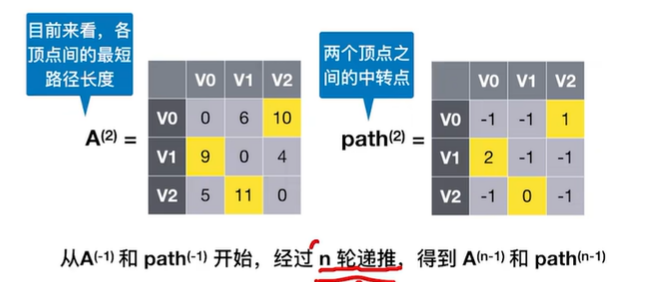
***
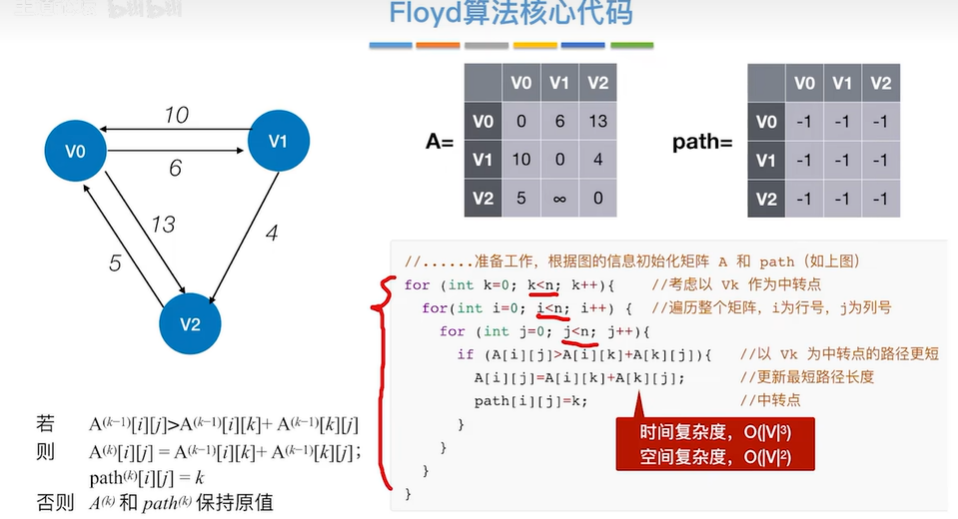
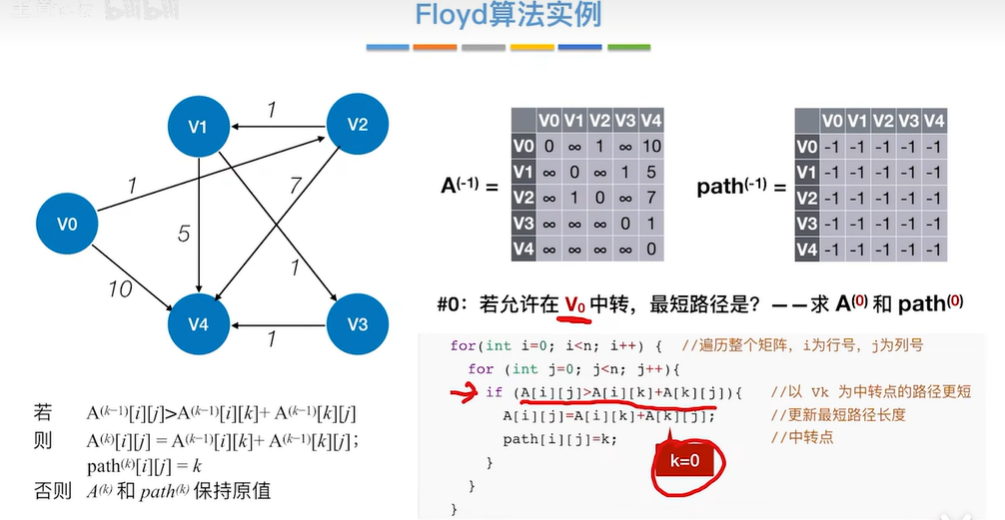


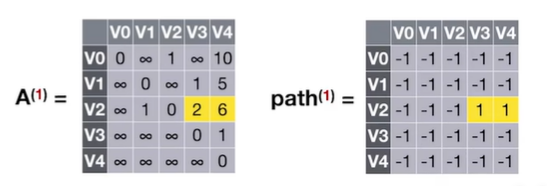
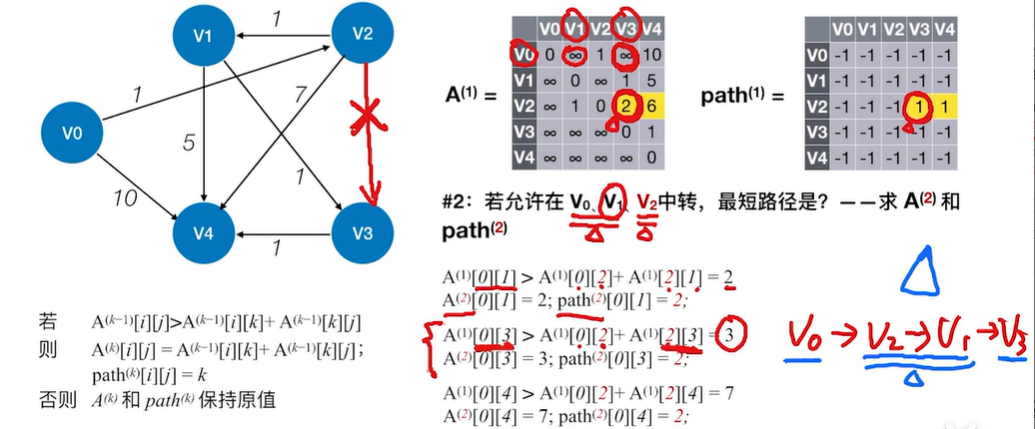
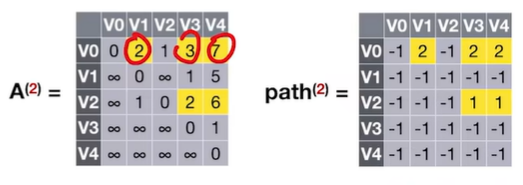
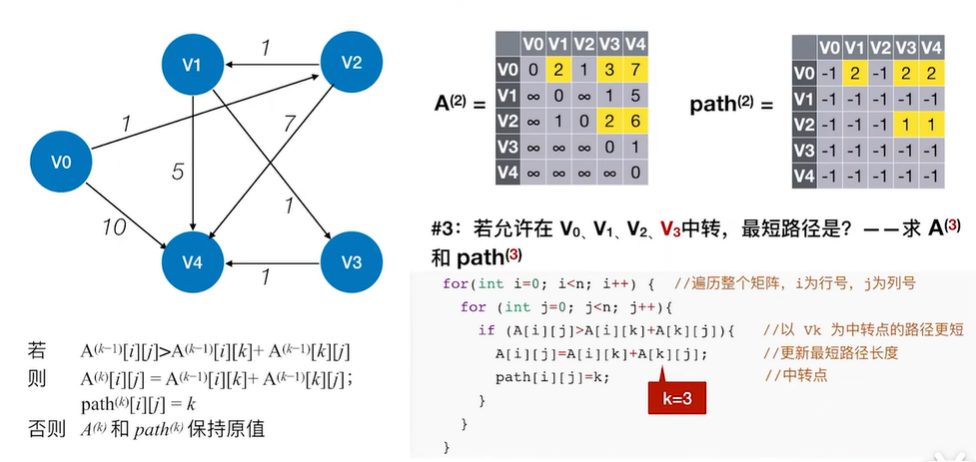

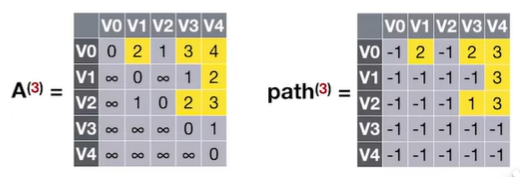
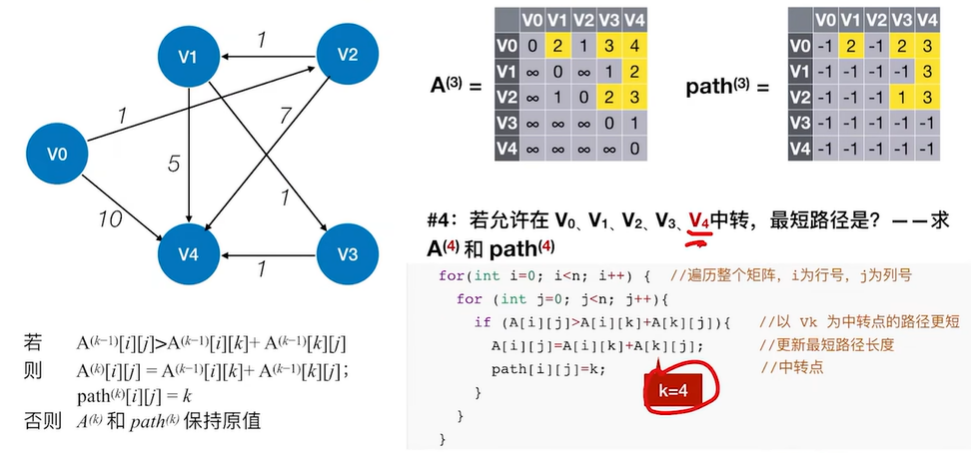

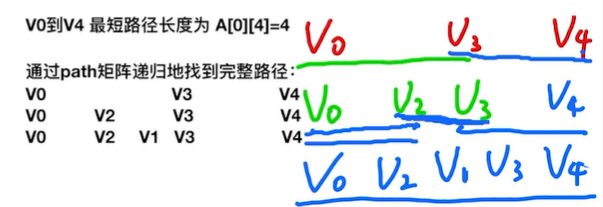
2.2.3.1 Floyd算法用于负权图
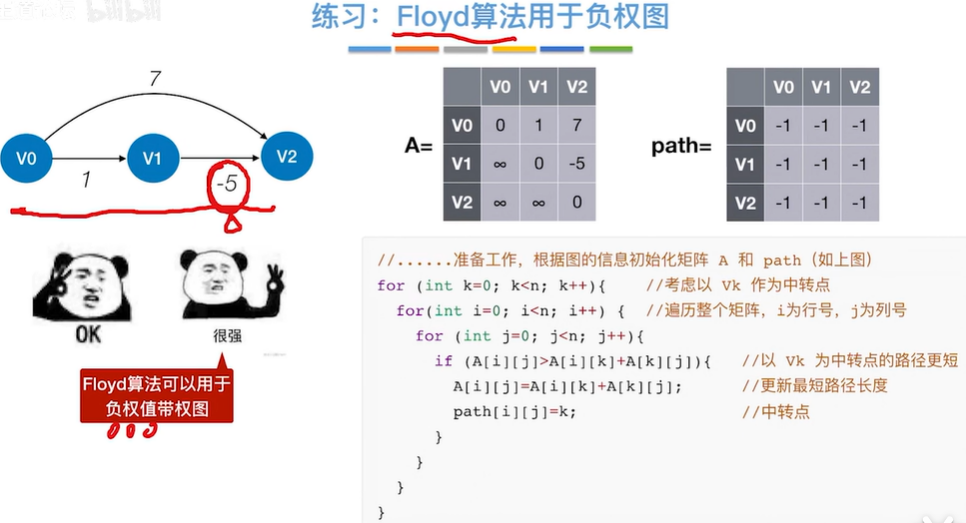

总结:
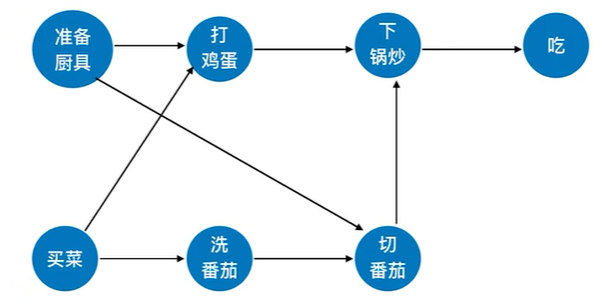
2.3 有向无环图(DAG)描述表达式
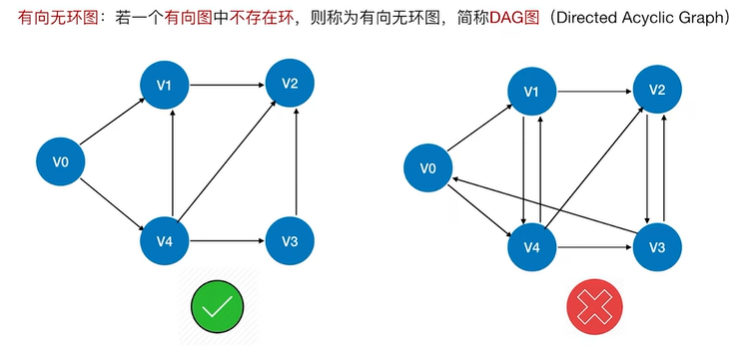
2.3.1 DAG描述表达式
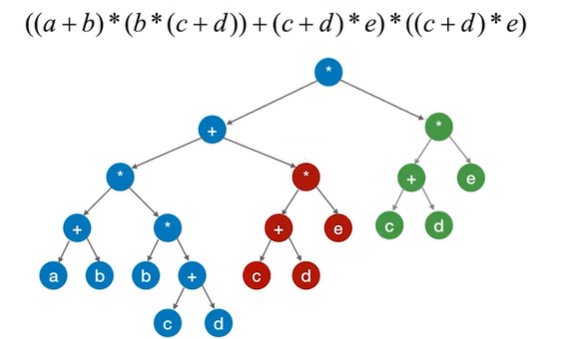
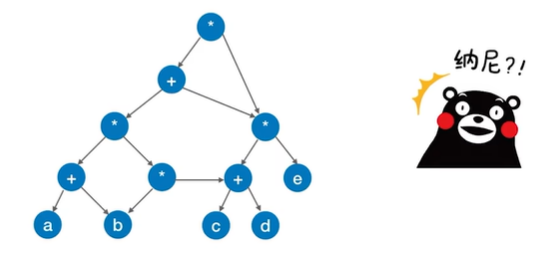
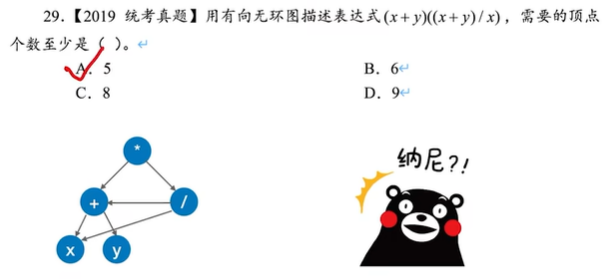
例题:

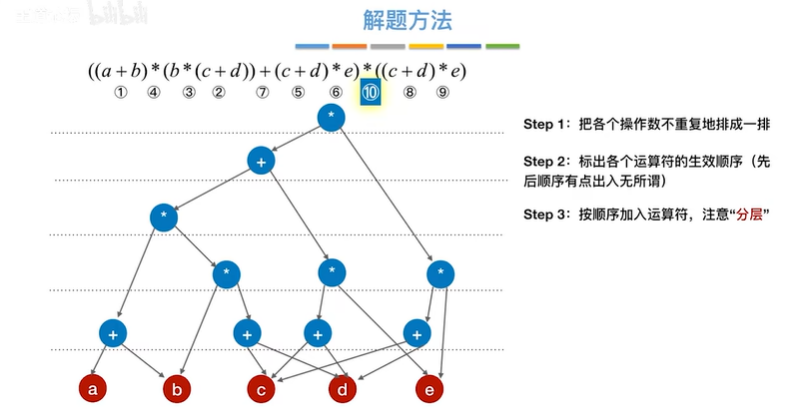
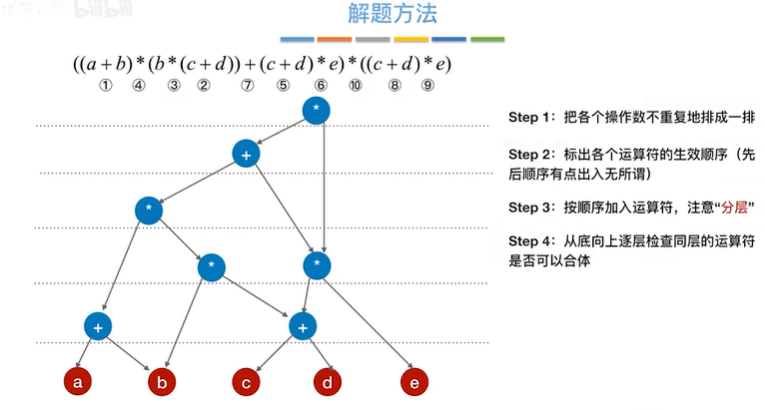
2.4 拓扑排序
拓扑排序 https://www.bilibili.com/video/BV1b7411N798/?p=66&share_source=copy_web&vd_source=d228985826b563972268952905224139
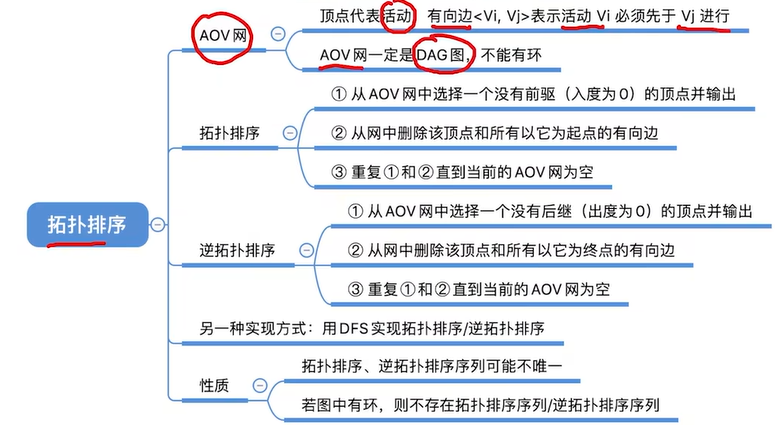
2.4.1 AOV网
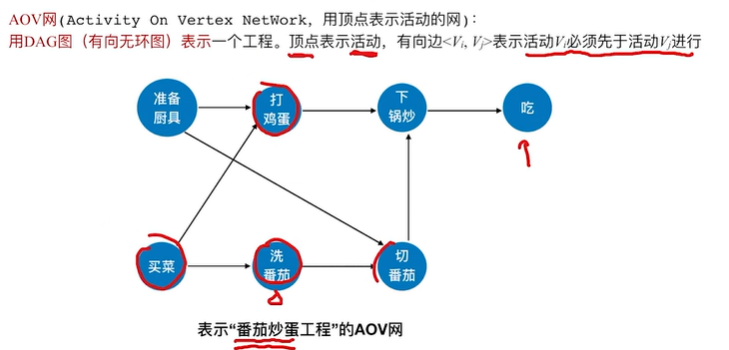
2.4.2 拓扑排序
拓扑排序:在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序:
① 每个顶点出现且只出现一次。
② 若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径。
或定义为:拓扑排序是对有向无环图的顶点的一种排序,它使得若存在一条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。
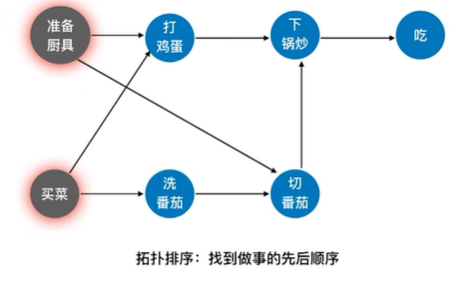

拓扑排序的实现:
①从AOV网中选择一个没有前驱(入度为0)的顶点并输出。
②从网中删除该顶点和所有以它为起点的有向边。
③重复①和②直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。(说明有回路)
2.4.3 对有回路的图进行拓扑排序
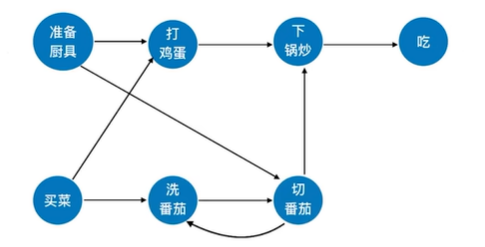
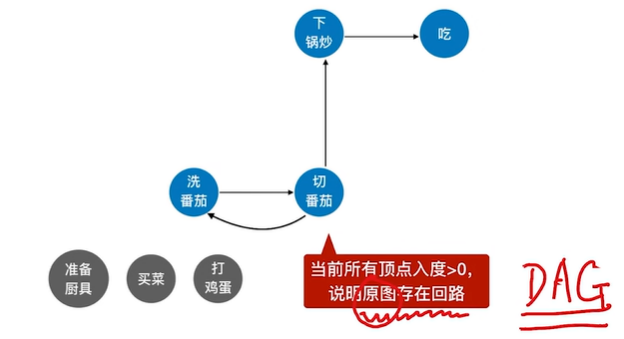
不能进行拓扑排序
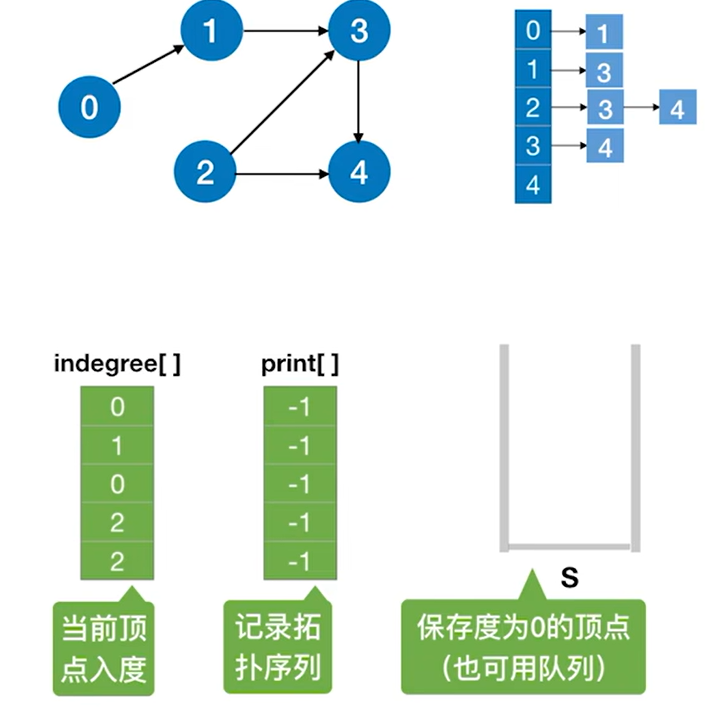
拓扑排序算法的实现如下:
#define MaxVertekNum 100 //图中顶点数目的最大值
typeder strtct ArcNcde{ //边表结点
int adjvex; //该弧所指向的顶点的位置
struct ArcNode* nextarc; // 指向下一条弧的指针
//InfoType info; //网的边权值
}ArcNode;
typedef struct VNode { //顶点表结点
vertexType data; //顶点信息
ArcNode* firstarc; // 指向第一条依附该顶点的弧的指针
}VNode, AdjList[MaxVertexNum];
typedef struct {
AdjList vertices; //邻接表
int vexnum, arcnum; //图的顶点数和弧数
}Graph; // Graph是以邻接表存储的图类型
bool Topologicalsort(Graph G) {
InitStack(S);
//初始化栈,存储入度为0的顶点
for (int i = 0; i < G.vexnum; i++)
if (indegree[i] == 0)
Push(s, i);//将所有入度为0的顶点进栈
int count = 0;
//计数,记录当前已经输出的顶点数
while (!IsEmpty(S)) {
/ 栈不空, 则存在入度为0的顶点
Pop(s, i);
/ 栈顶元素出栈
print[count++] = i;
//输出顶点i
for (p = G.vertices[i].firstarc; p; p = p->nextarc) {
//将所有i指向的顶点的入度减1,并且将入度减为0的顶点压入栈S
v = p->adjvex;
if (!(--indegree[v]))
Push(s, v);
l / 入度为0,则入栈
}//while
if (count < G.vexnum)
return false;
//排序失败,有向图中有回路
else
returntrue;
//拓扑排序成功
}

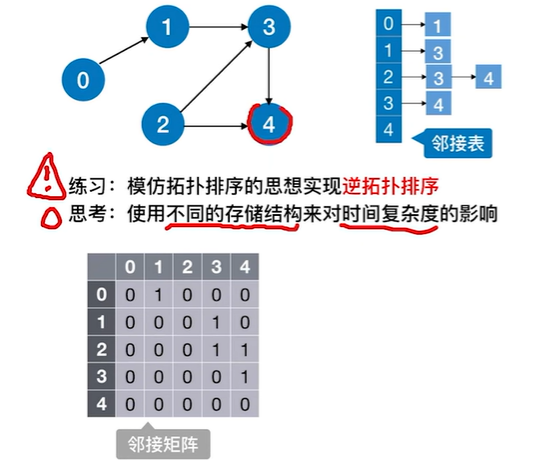
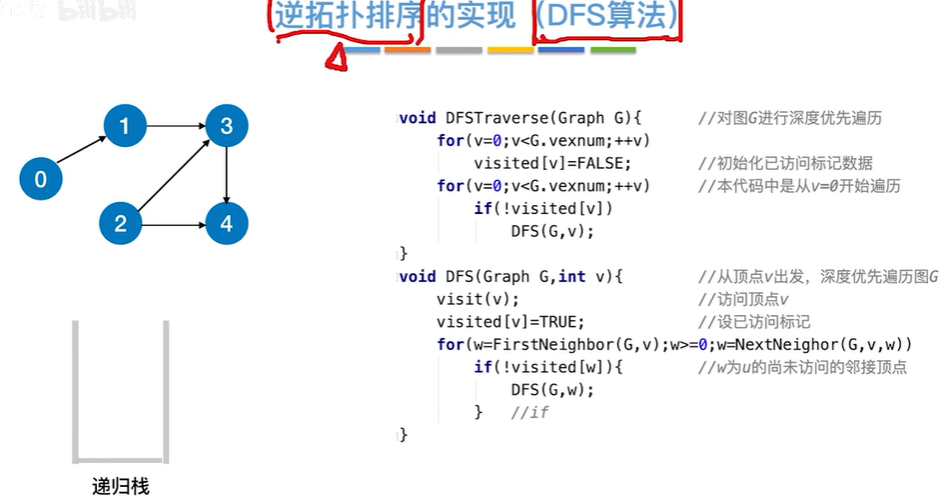
2.4.4 逆拓扑排序
对一个AOV网,如果采用下列步骤进行排序,则称之为逆拓扑排序:
① 从AOV网中选择一个没有后继(出度为0)的顶点并输出。
② 从网中删除该顶点和所有以它为终点的有向边。
③重复①和②直到当前的AOV网为空。


2.5 关键路径
教程:关键路径 https://www.bilibili.com/video/BV1b7411N798/?p=67&share_source=copy_web&vd_source=d228985826b563972268952905224139
2.5.1 AOE网
在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称AOE网(Activity On Edge NetWork)
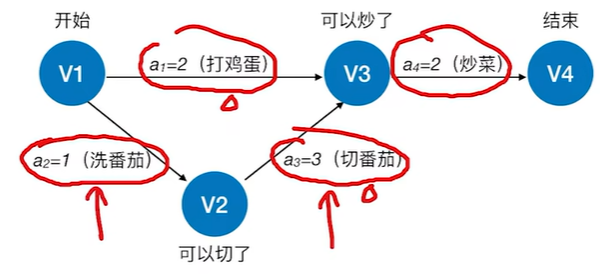
AOE网具有以下两个性质:
①只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始;
②只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生。另外,有些活动是可以并行进行的
在AOE网中仅有一个入度为o的顶点,称为开始顶点(源点),它表示整个工程的开始;
也仅有一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。
从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动
完成整个工程的最短时间就是关键路径的长度,若关键活动不能按时完成,则整个工程的完成时间就会延长
2.5.2 关键路径
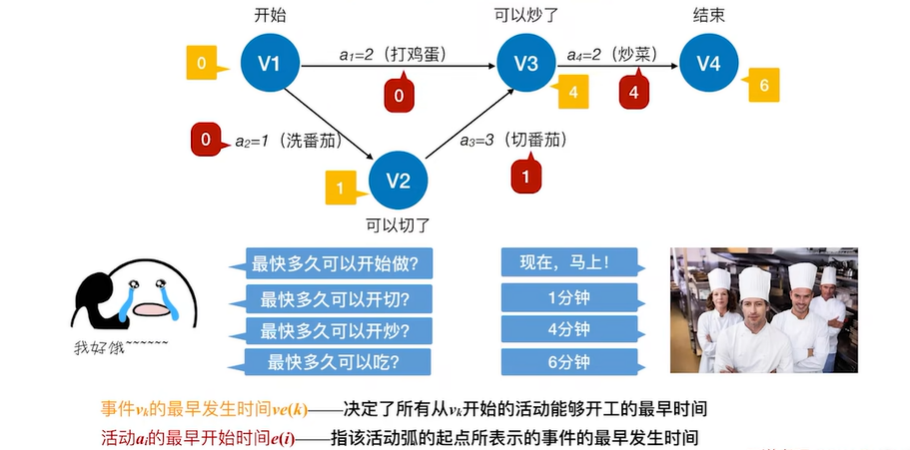


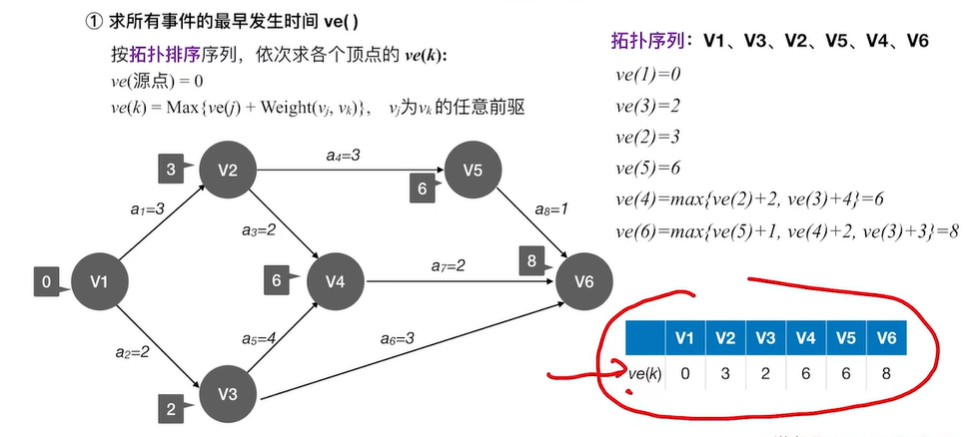
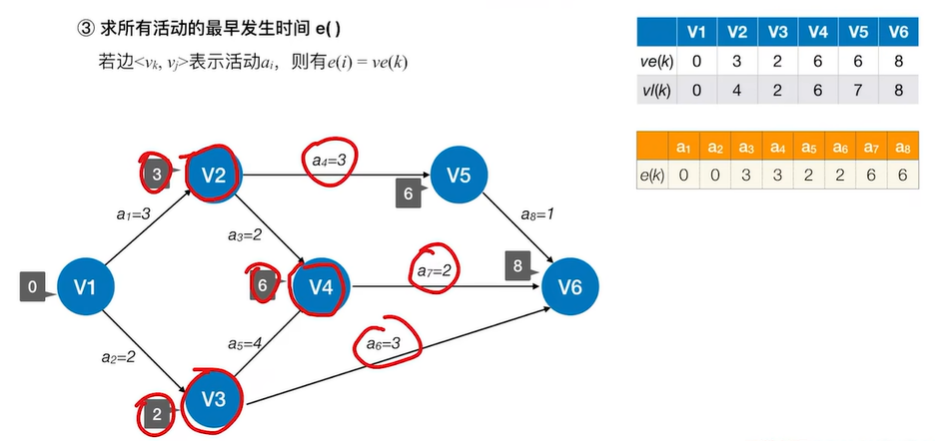
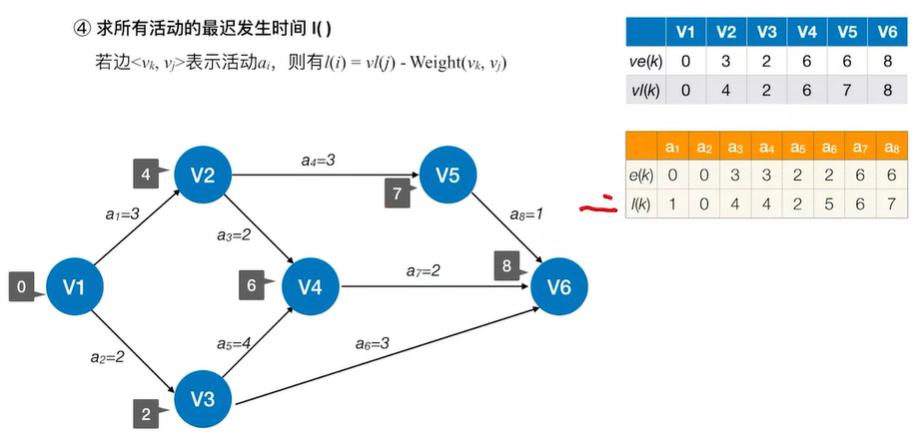
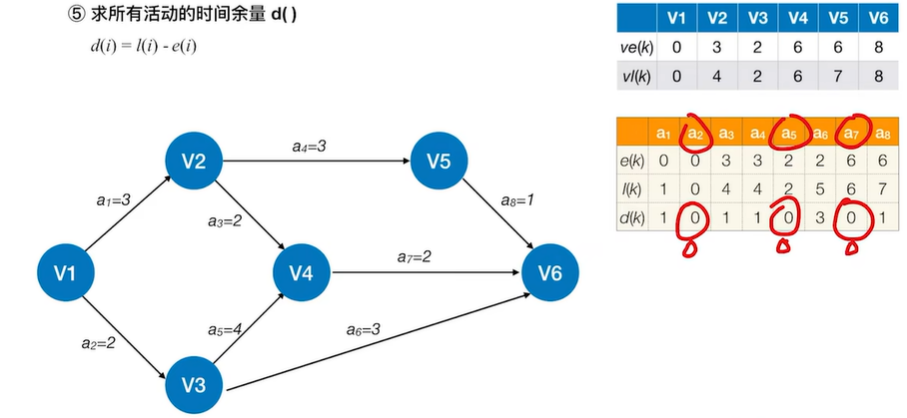
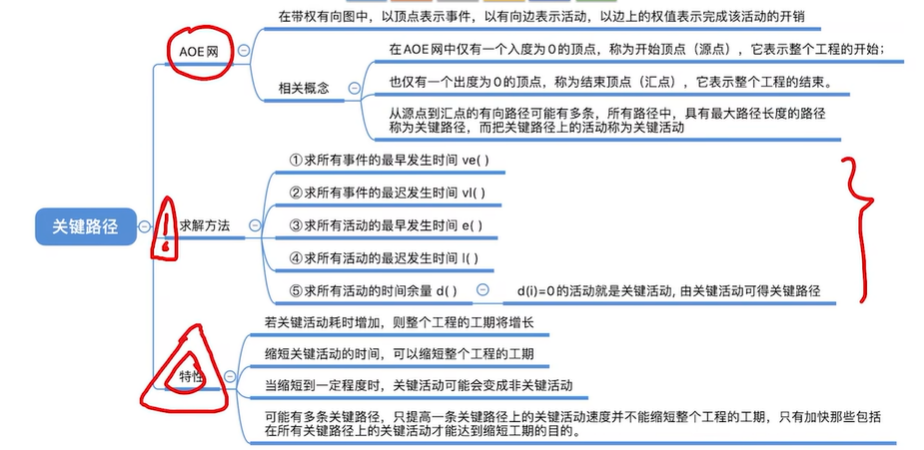
2.5.3 求关键路径的步骤
- 事件Vk的最早发生时间ve(k)


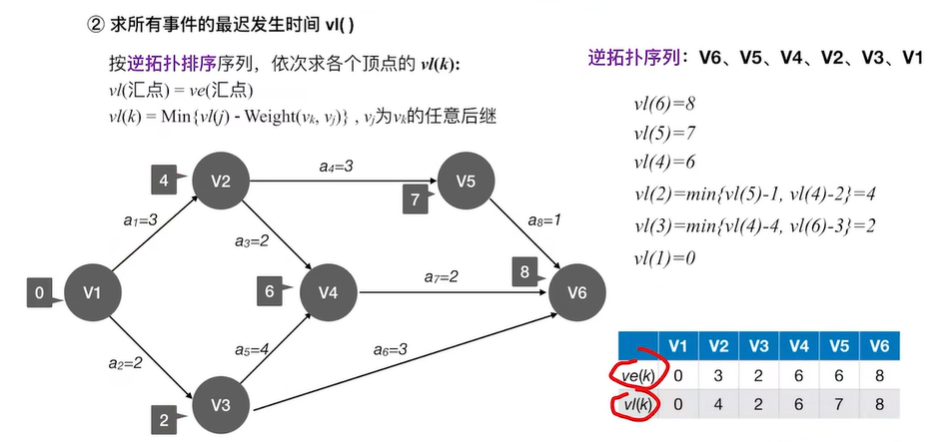




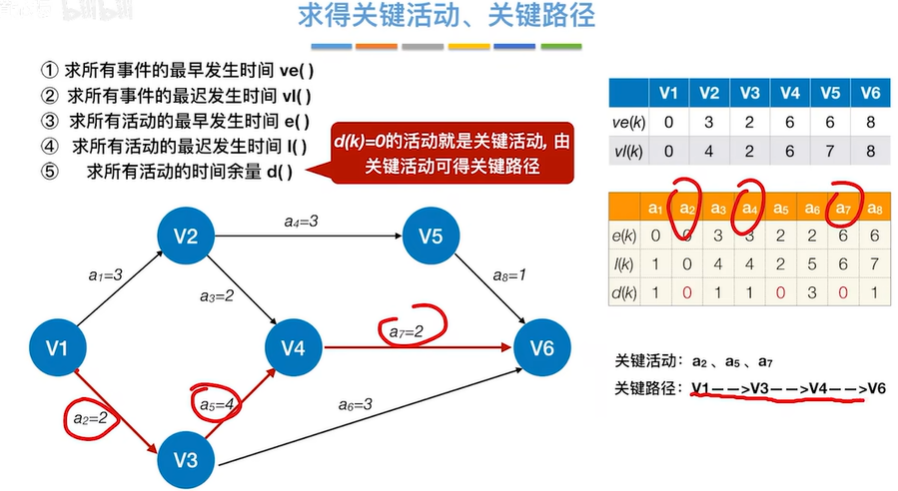
2.5.4 关键活动、关键路径的特性
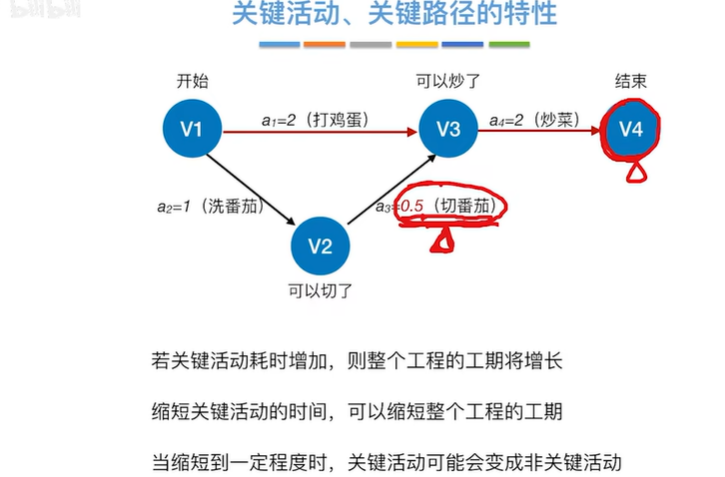
可能有多条关键路径,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。

![[附源码]java毕业设计人口老龄化社区服务与管理平台](https://img-blog.csdnimg.cn/5752d36f256241b291fd5f8cb759171e.png)




![第五届“传智杯”全国大学生计算机大赛(练习赛) [传智杯 #5 练习赛] 复读](https://img-blog.csdnimg.cn/bc42e9d2df6d4415b16fd3fc72afd226.png)