文章目录
- 堆
- 概念
- 堆的创建
- 堆向下调整
- 堆的插入
- 堆的删除
- 堆排序
- 整体代码(创建堆(向下调整),堆的插入,堆的删除,堆排序)
- TOPK
- PriorityQueue特性
堆
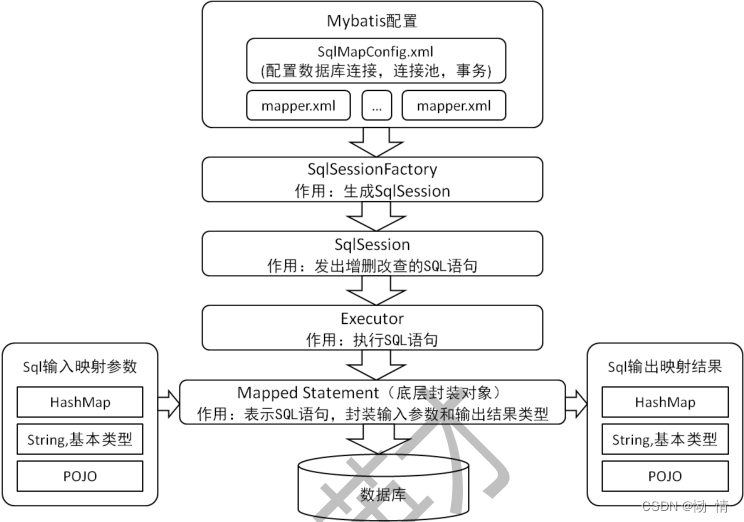
概念
如果有一个关键码的集合K=k0,k1,k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki<= K2i+1且Ki<=K2i+2(Ki>=K2i+1且K>=K2i+2)i=0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
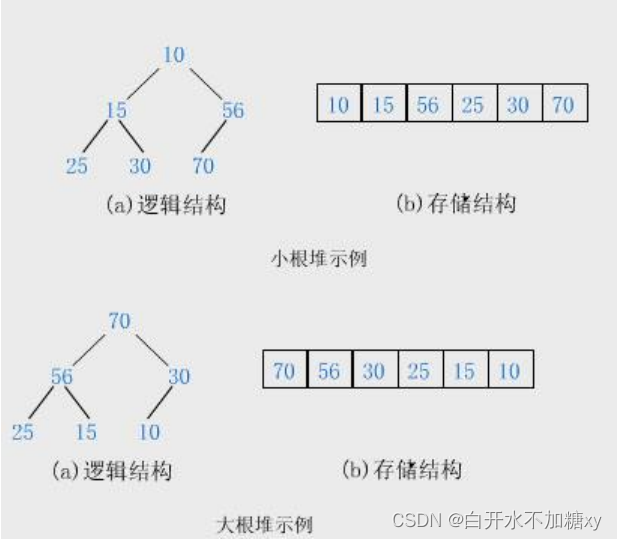
从堆的概念可知,堆是一提完全二叉树,因此可以层序的规则采用顺序的方式来高效存储。
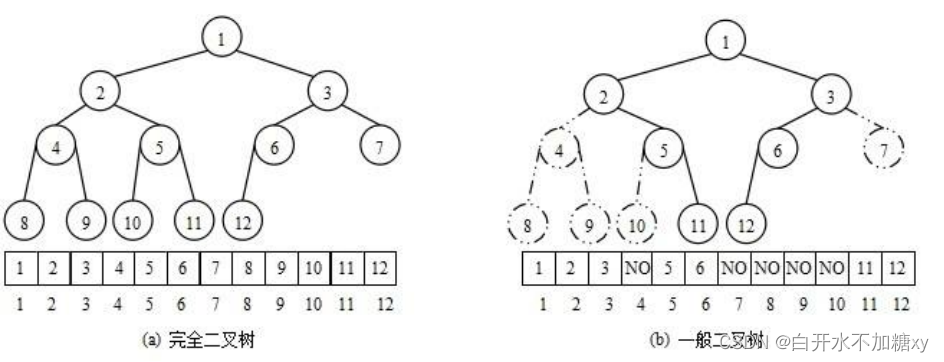
实质:
1.逻辑上是一棵完全二叉树
可以按照层序的方式平铺在数组中。
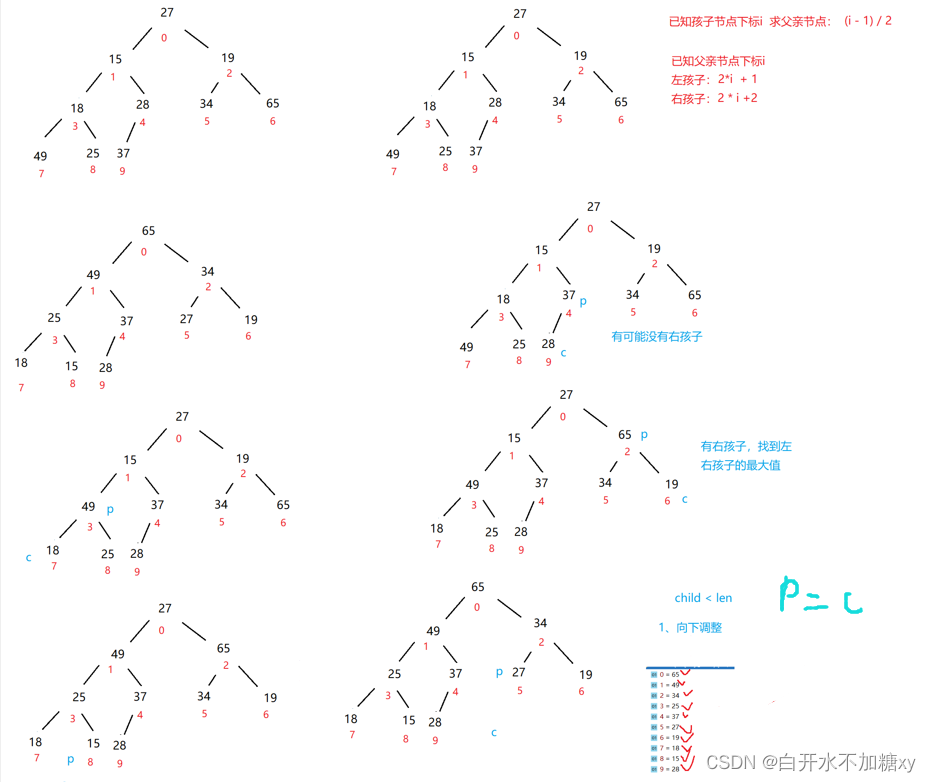
已知parent 的下标:1) left = 2 * parent + 1;
2)right = 2 * parent +2 ;
已知child (不分左右)的下标:parent = ( child -1 ) / 2
2.物理上是一个数组
3.满足任意位置的值大于等于它左右孩子的值 - -大堆
满足任意位置的值小于等于它左右孩子的值 - - 小堆
堆的创建
堆向下调整
从根节点开始的向下调整算法可以把它调整
成一个小堆。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
int[] array = { 27,15,19,18,28,34,65,49,25,37 };
生成大根堆:
堆的插入
先插入一个80到数组的尾上,再进行向上调整算法,直到满足堆。
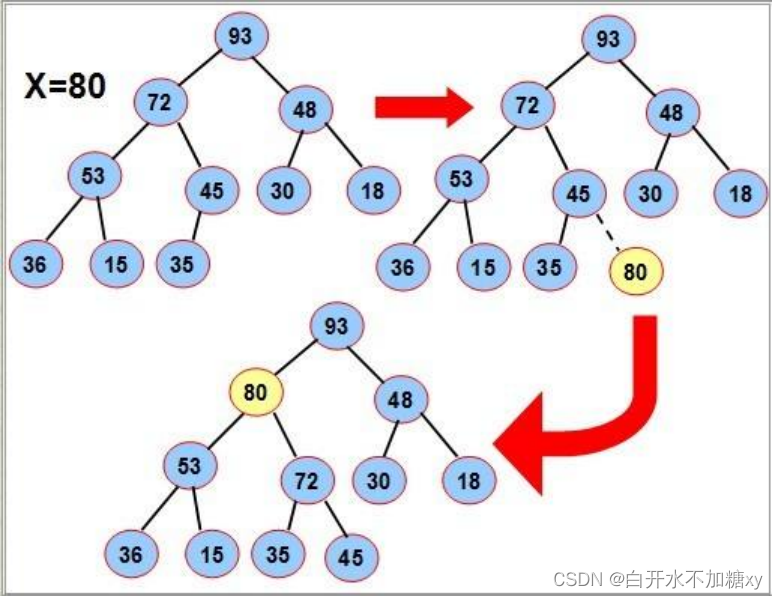
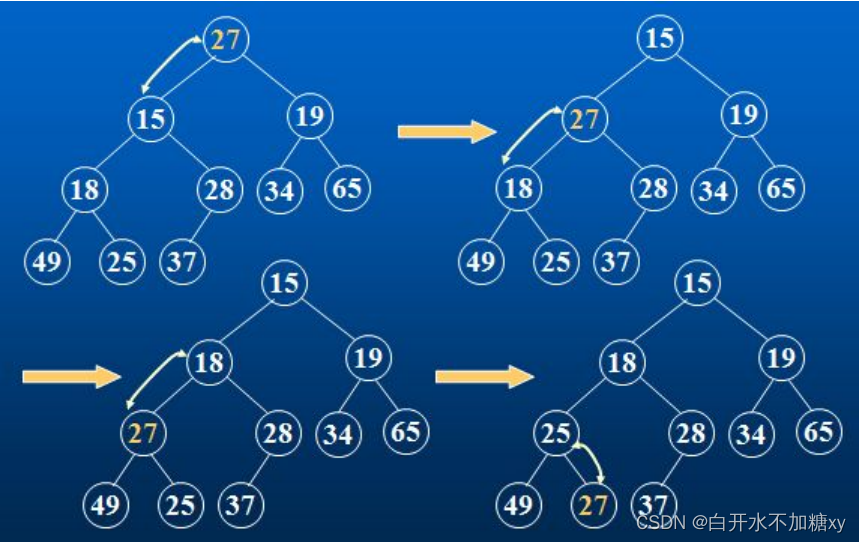
堆的删除
1.0下标和最后一个元素交换
2.向下调整0下标这棵树即可
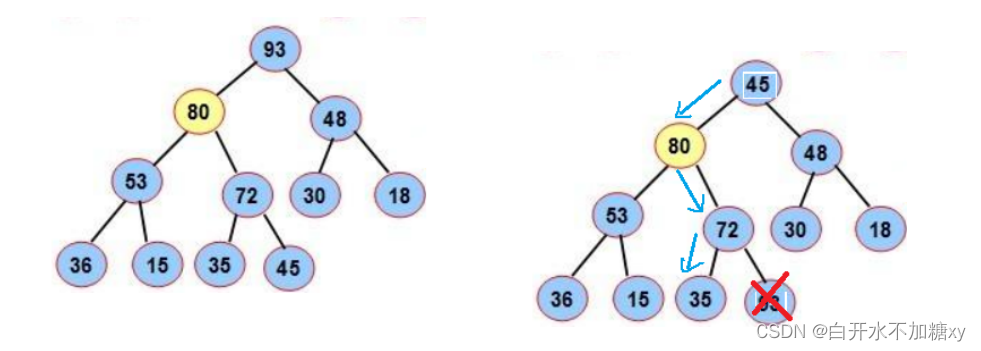
堆排序
1.从小到大排序——升序
- 需要创建一个大根堆
- 堆顶元素不断与堆尾元素(end下标)进行交换,直到end<=0,即堆尾元素遍历到堆顶。
- 交换后,从堆顶再向下调整
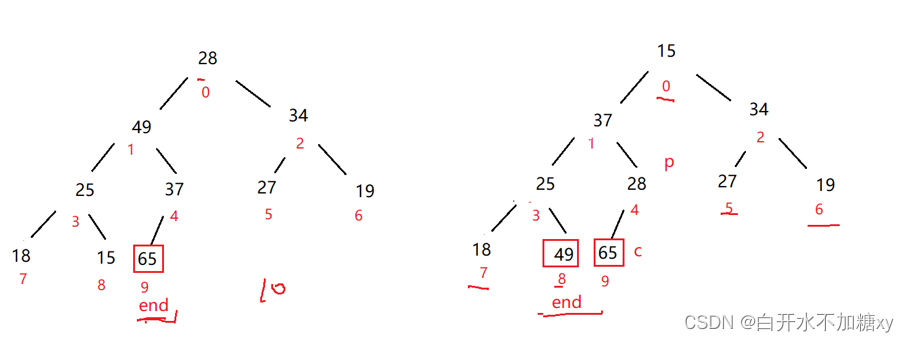
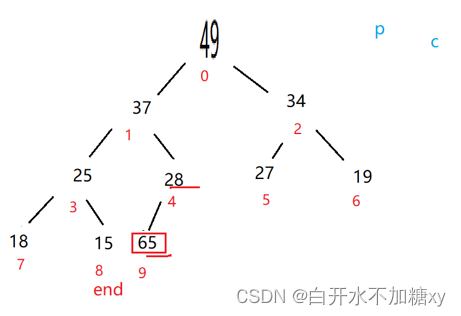
2.从大到小排序——降序
整体代码(创建堆(向下调整),堆的插入,堆的删除,堆排序)
public class TestHeap {
public int[] elem;
public int usedSize;
public TestHeap() {
this.elem = new int[10];
}
/**
* 向下调整
* parent:每次调整的根节点
* len:每次的结束位置
*/
public void shiftDown(int parent,int len) {
int child = (2 * parent)+1;
//说明这棵树没有调整完
while (child < len) {
//如果有右孩子 你才去判断
if(child+1 < len && elem[child] < elem[child+1]) {
child++;
}
//child下标 一定是左右孩子最大值的下标
if(elem[child] > elem[parent]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}
public void createHeap(int[] array) {
//this.elem = Arrays.copyOf(array,array.length); 不算
for (int i = 0; i < array.length; i++) {
elem[i] = array[i];
this.usedSize++;
}
for (int i = (usedSize-1-1)/2; i >= 0 ; i--) {
shiftDown(i,usedSize);
}
}
/**
* 向上调整
* @param child
*/
public void shiftUp(int child) {
int parent = (child-1) / 2;
while (parent >= 0) {
if(elem[child] > elem[parent]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
child = parent;
parent = (child-1)/2;
}else {
break;
}
}
}
/**
* 插入一个元素到堆中
* @param val
*/
public void push(int val) {
if(isFull()) {
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);//扩容
}
this.elem[this.usedSize] = val;
this.usedSize++;
shiftUp(this.usedSize-1);
}
public boolean isFull() {
return this.usedSize == this.elem.length;
}
/**
* 出队,删除堆顶元素.
*/
public int pop() {
if(isEmpty()) {
throw new HeapEmptyException("堆为空!");
}
int tmp = elem[0];
elem[0] = elem[this.usedSize-1];
elem[this.usedSize-1] = tmp;
this.usedSize--;
shiftDown(0,this.usedSize);
return tmp;
}
public boolean isEmpty() {
return this.usedSize == 0;
}
/**
* 堆排序
*/
public void heapSort() {
int end = usedSize-1;
while (end > 0) {
int tmp = elem[end];
elem[end] = elem[0];
elem[0] = tmp;
shiftDown(0,end);
end--;
}
}
public void heapSort1() {
//createHeap();创建一个大根堆
int end = usedSize-1;
while (end > 0) {
int tmp = elem[end];
elem[end] = elem[0];
elem[0] = tmp;
shiftDown(0,end);
end--;
}
}
}
TOPK
代码可参考之前的博客: TOPK

PriorityQueue实现非基本类型的建堆、TOPK操作:
1.实现Comparable 接口 重写compareTo()方法,设计规则实现比较
注意:
@Override
public int compareTo(Student o) {
return this.age-o.age;//小堆
//return o.age-this.age;//大堆
}
2.自己写比较器
//比较器
class AgeComparator implements Comparator<Student>{
@Override
public int compare(Student o1, Student o2) {
return o2.age-o1.age;
}
}
整体参考代码:
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
/**
* @Author 12629
* @Date 2022/3/24 16:18
* @Description:
*/
//实现Comparable 接口 重写compareTo()方法,设计规则通过年龄比较
/*class Student implements Comparable<Student>{
public String name;
public int age;
public Student(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "Student{" +
"name='" + name + '\'' +
", age=" + age +
'}';
}
@Override
public int compareTo(Student o) {
return this.age-o.age;//小堆
//return o.age-this.age;//大堆
}
}*/
class Student {
public String name;
public int age;
public Student(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "Student{" +
"name='" + name + '\'' +
", age=" + age +
'}';
}
}
//比较器
class AgeComparator implements Comparator<Student>{
@Override
public int compare(Student o1, Student o2) {
return o2.age-o1.age;
}
}
public class TestDemo {
/**
* 前K个最小的元素
* @param array
*/
public static int[] topK(int[] array,int k) {
//相当于是一个类,实现了Comparator接口,并且重写了compare接口。匿名内部类
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;//大堆,否则小堆
}
});
//PriorityQueue<Integer> maxHeap2 = new PriorityQueue<>(k,((o1, o2) -> {return o2-o1;}));//lamda表达式上述写法
for (int i = 0; i < array.length; i++) {
if(maxHeap.size() < k) {
maxHeap.offer(array[i]);
}else {
//1、先获取堆顶元素
int top = maxHeap.peek();
if(top > array[i]) {
maxHeap.poll();
maxHeap.offer(array[i]);//maxHeap插入元素,并调整堆为大堆
}
}
}
int[] ret = new int[k];
for (int i = 0; i < k; i++) {
ret[i] = maxHeap.poll();//前K个最小的元素
}
return ret;
}
public static void main(String[] args) {
int[] array = {1,2,31,4,51,16,7};
int[] ret = topK(array,3);
System.out.println(Arrays.toString(ret));
}
public static void main4(String[] args) {
AgeComparator ageComparator = new AgeComparator();
PriorityQueue<Student> students = new PriorityQueue<>(ageComparator);//传入比较器ageComparator参数。默认的话,比较器为null
students.offer(new Student("bit",19));
students.offer(new Student("gaobo",9));
//建堆
System.out.println(students);
}
public static void main3(String[] args) {
//默认容量是11 到底是大根堆 还是 小根堆-> 默认小根堆
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(10);
priorityQueue.offer(8);
priorityQueue.offer(30);
priorityQueue.offer(5);
System.out.println(priorityQueue.poll());//5
System.out.println(priorityQueue.peek());//8
}
}
PriorityQueue特性
- PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出ClassCastException异常
- 不能插入null对象,否则会抛出NullPointerException
- 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
- 插入和删除元素的时间复杂度为O(log2N)
- PriorityQueue底层使用了堆数据结构,(注意:此处大家可以不用管什么是堆,后文中有介绍)7.PriorityQueue默认情况下是小堆—即每次获取到的元素都是最小的元素