学习是一种基础性的能力。然而,“吾生也有涯,而知也无涯。”,如果学习不注意方法,则会“以有涯随无涯,殆矣”。
学习就像吃饭睡觉一样,是人的一种本能,人人都有学习的能力。我们在刚出生的时候,什么也不知道,是一张真正的白纸,我们靠学习的本能,学会了走路、说话、穿衣服…后来,我们上学了,老师把书本上的知识一点一点灌输到我们的脑子里,我们掌握的知识越来越多,与此同时,我们学习能力却好像越来越差了,习惯了被别人喂饱,似乎忘记了怎么来喂自己了。
学习本来只是一种本能,算不上什么能力,然而,经过二十多年的不断学习,学习反而成为了一种真正的能力,因为我们慢慢失去了它,它就更显得珍贵。
作为一个程序员,不断的学习更是重要,不学新的知识就迟早会被淘汰掉
算法能力是每一个程序员的基本功,只懂模型不懂算法,注定只是一个“绣花枕头”,而非真正的工程师。
众所周知,程序员求职面试必考算法,题刷得好,拿Offer更有优势。但是,没有坚实的算法知识体系储备,没有长期持之以恒算法题目训练,很难脱颖而出。
所以,为有需要的朋友们送上一套**【算法与数据结构突击手册】的福利。按照算法知识体系**,精心筛选leetcode、HDU等平台1000+经典题目。
话不多说直接上文档展示图:
字符串
- 旋转词
- 单词间逆序
- 字符串循环左移
- 字符串数组拼接为最小字符串
- 变形词
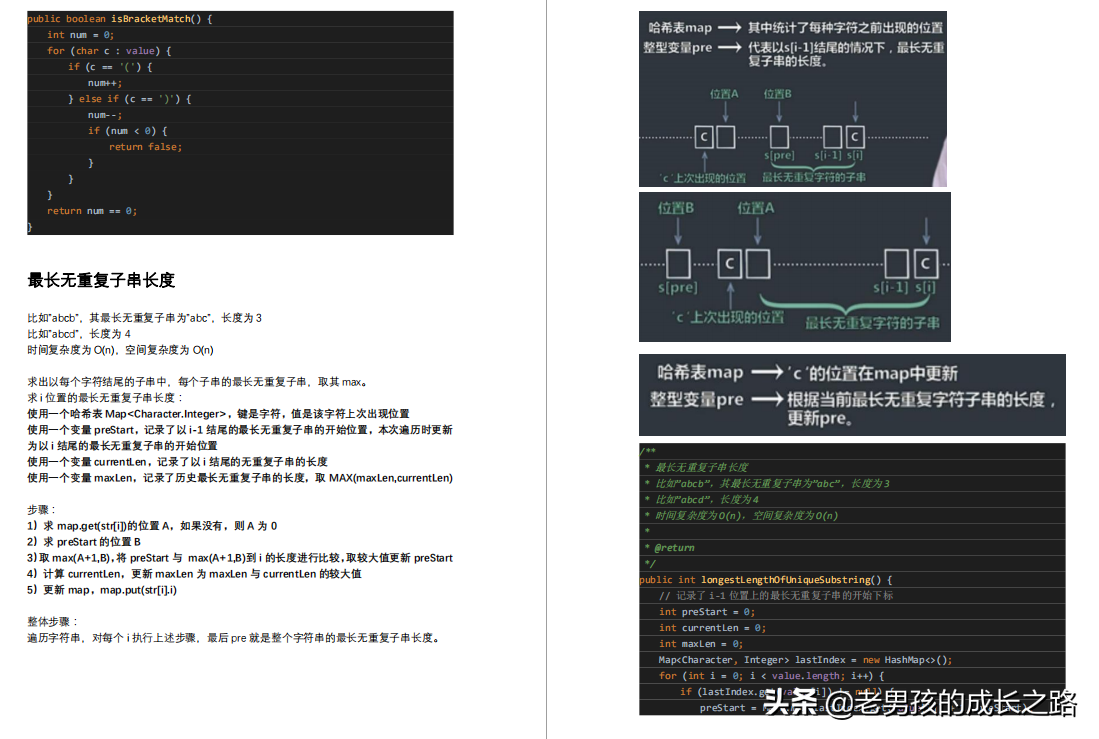
- 括号匹配
- 最长无重复子串长度
- 正则表达式匹配
- 替换空格
- 第一个只出现一次的字符
- atoi
二叉树
- 非递归先中后序遍历
- 层序遍历
- 换行层序遍历
- 层序遍历至二维数组
- 之字形打印二叉树
- 二叉树的深度(递归;非递归)
- 前序遍历重建二叉树
- 翻转二叉树
- 判断一棵二叉树是否是另-棵二叉树的子树
- 平衡二叉树判断(后序遍历)
- 二叉搜索树判断(4种算法,中序遍历最优)
- 完全二叉树判断( 层序遍历)
- 求任意节点的后继节点
- 折纸的折痕(RVL中序遍历)
- 二叉搜索树查错(中序遍历)
- 二叉树节点间最大距离(后序遍历)
- 二叉树中的最大二叉搜索子树(后序遍历)
- 前中序遍历重建二叉树
- 二叉树判断是否对称(先序遍历)
- 二又树的所有路径(先序遍历)
- 二叉树中和为某值的所有路径
- 二叉搜索树转为有序双向链表(中序遍历)
- 二叉搜索树的第k个节点(从小到大)
- 二叉树父节点(先序遍历)
- 二叉树第k层节点个数
- 有序数组重建BST/AVL
- 有序链表重建BST/AVL
- (Skip)二叉树中两节点的最小公共祖先 LeastCommonAncestor LCA
- 二叉树节点间的最短路径
- 递归打印文件和目录

排序
- 快速排序(拆分为qui ckSor t和parti ti on的版本)
- 快速排序非递归实现
- 数组中出现次数超过一半的数字/中位数 ( 类似于快速排序)
- 无序数组Top K
- 无序数组中的第k大元素(基于partition)
- 数据流中的中位数
- 两个有序数组找中位数( 待解决)
- 几乎有序的数组排序(改进后的堆排序)
- 有序数组合并
- 有序矩阵搜索
- 需要排序的最短子数组长度
- 三色排序(类似快排)
- 数组中的逆序对(待解决)
- 有序数组中和为某值的数对( 2Sum )
- 3Sum
- 数组中所有数对的最大差值
- (Skip)数组中邻近数对的最大差值
二分搜索
- 简单二分搜索
- 二分搜索最小位置
- 二分搜索最大位置
- 有序数组中某个数字的出现次数
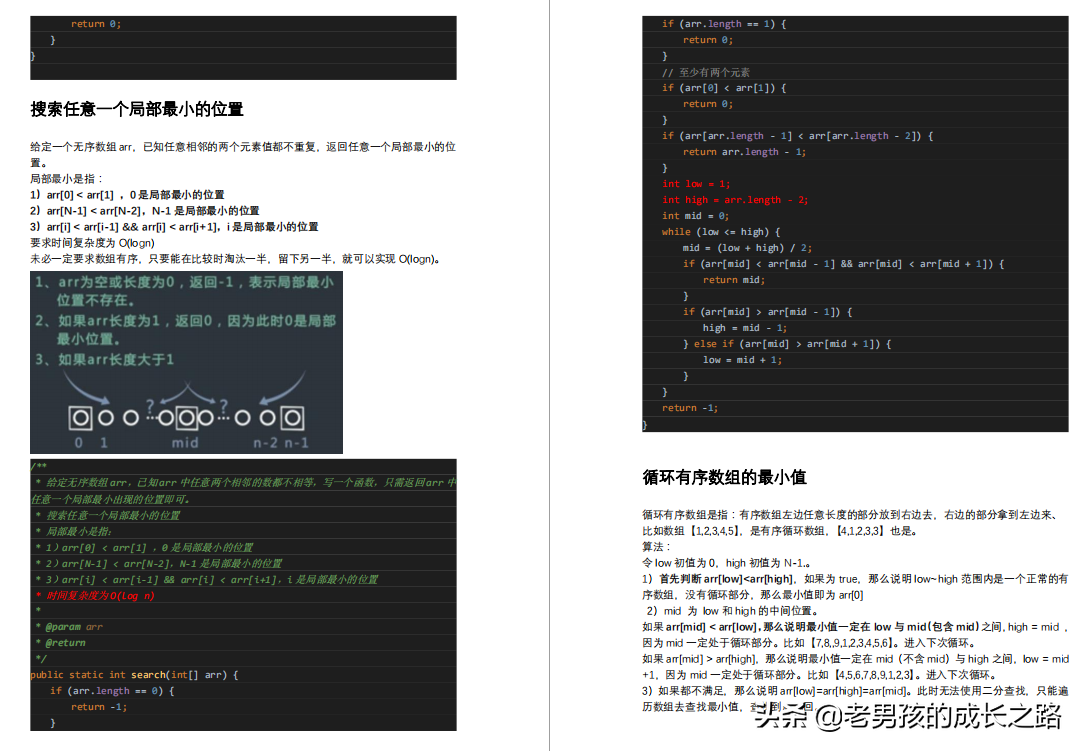
- 搜索任意一个局部最小的位置
- 循环有序数组的最小值
- 最左侧『数值和下标相等』的元素
- 完全二叉树计数
- 快速N次方
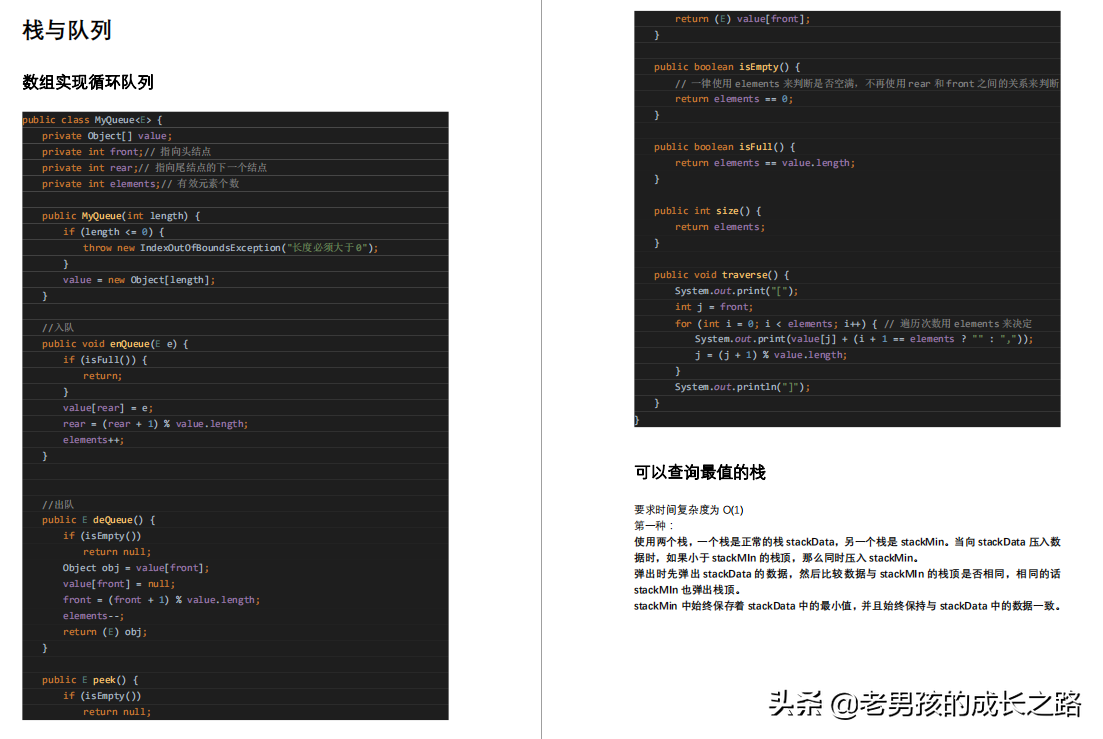
栈与队列
- 数组实现循环队列
- 可以查询最值的栈
- 双栈实现队列
- 栈逆序
- 双栈排序
- 滑动窗口
- (Skip)数组转类似于大顶堆的二叉树MaxTree
- 调整数组顺序使奇数位于偶数前面
- 栈的压入、弹出序列是否匹配
- 逆序打印链表
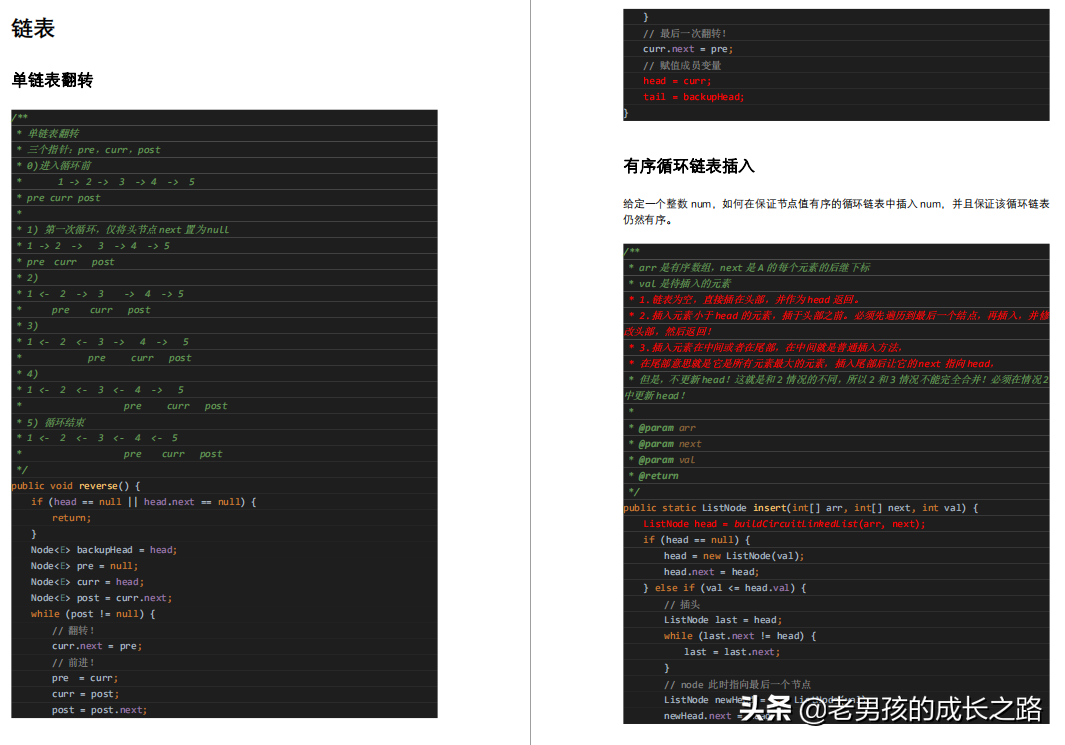
链表
- 单链表翻转
- 有序循环链表插入
- 单链表删除当前节点
- 链表分化(按与某值比较结果分化为三条小链表)
- 调整链表顺序使奇数位于偶数前面
- 两个有序链表的公共值
- 链表每K个节点间逆序
- 链表删除指定值
- 无序链表删除重复节点
- 有序链表删除重复节点
- 判断链表是否为回文
- 简单链表复制
- 复杂链表复制
- 链表判环
- 无环单链表判交
- 有环单链表判交
- 单链表判交(可能有环也可能无环)
- 约瑟夫问题
- 找到倒数第k个节点(双指针,一指针先移动k步)
- 删除倒数第k个节点
- 合并两个有序链表
- 单链表归并排序
位运算
- 交换(异或)
- 比较(移位,与,异或)
- 寻找数组中唯一出现奇数次数的元素(异或)
- 寻找数组中唯二出现奇数次数的元素(异或)
- 寻找乱序后的连续数字[1,N]中缺失的数字/数组中唯一的重复数字
- 二进制中1的个数
- 判断是否是2的幂次
- 求一个数的临近的较大的2的幂次(HashMap)
- (Skip)数字序列中某一位的数字
- 寻找重复数字(整数范围内) bitmap
- 无序数组中数字的重复次数hashmap
- 求一个字符集合的所有可能子集 int as bitmap
- 布隆过滤器

排列组合
- 方格移动
- 全排列
- 打印从1到最大的n位数

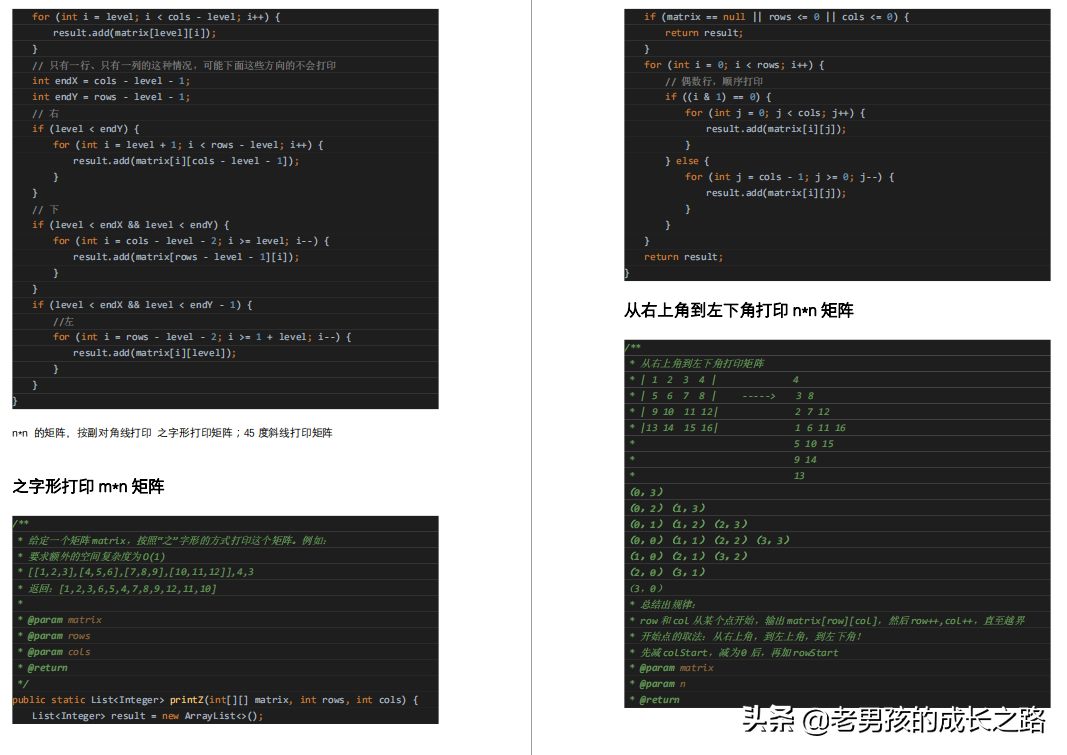
矩阵
- 口顺时针打印 m*n矩阵
- 口之字形打印 m*n矩阵
- 口从右上角到左下角打印 n*n 矩阵
- 口从左上角到右下角打印 n*n矩阵
概率
- 两强相遇概率
- 蚂蚁碰头
- 随机函数
- 随机01
- 随机数组打印

海量数据
- 哈希函数
- Map-Reduce
- 词频统计——哈希表
- 词频统计——Trie树(还可以查询、前缀匹配、排序、去重)
- 海量数据解题关键
- 10亿IP地址排序/10亿数字排序
- 10亿人的年龄排序
- 20亿数字中出现次数最多的数
- 40亿数字中在42亿范围内没有出现过的数
- 百亿词中出现次数最高的10个

动态规划 Dynamic Programming DP
- 准则
- 解法
- 斐波那契序列/跳台阶
- 换零钱
- 最大连续子序列和
- 最长上升子序列(不必连续) LIS longest increasing subsequence
- 最长公共子序列(不必连续) LCS longest common subsequence
- 01背包
- 矩阵最小路径和
- 剪绳子 O(n^2)
- 最长回文子串(待解决)
- 数对之差的最大值(待解决)

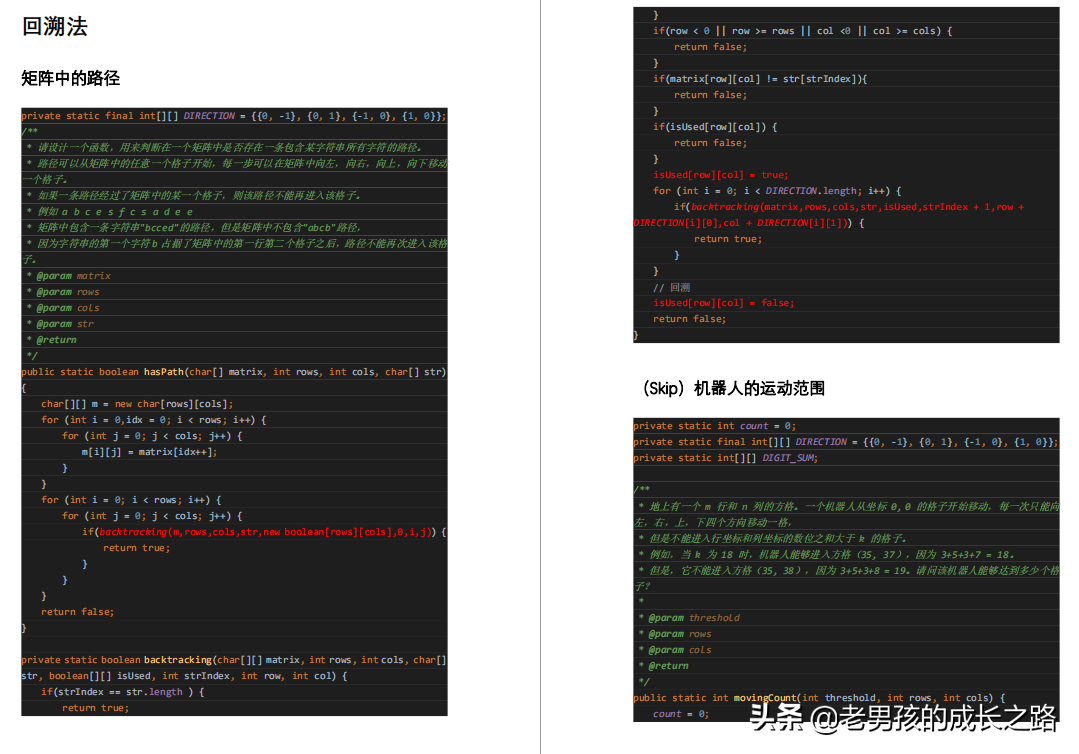
回溯法
- 矩阵中的路径
- (Skip)机器人的运动范围
- 数组中和为某值的所有子序列(待解决)
其他
- 汉诺塔
- 求素数/质数
- 递归求阶乘
- 求最大的n,要求n的阶乘范围在int内
- 数组中元素范围为[0,N-1],找出所有的/任意一个重复数字
- 并集、交集、差集
- 最小公倍数和最大公约数
- 判断是否是回文数
- 数组中第二大的数字
- 数组中重复次数最多的数 hashmap

总目录展示

面试官为什么爱问数据结构与算法,答案很简单:
- 算法能力能够准确辨别一个程序员的技术功底是否扎实;
- 算法能力是发掘程序员的学习能力与成长潜力的关键手段;
- 算法能力能够协助判断程序员在面对新问题时,分析并解决问题的能力;
- 算法能力是设计一个高性能系统、性能优化的必备基础。
BAT 等国内的一线名企,在招聘工程师的过程中,对算法和数据结构都会重点考察。但算法易学难精,我的很多读者技术能力不错,但面试时总败在算法这一关,拿不到好 Offer。但说实话,数据结构和算法花点时间,用对方法,很容易解决。