四、龙贝格求积公式（第三次课）

1.梯形法的递推化 (变步长求积法)

课堂推导：（在考试范围之内！）


收敛太慢。

2.龙贝格算法

如何提高收敛速度以节省计算量是龙贝格算法要讨论的中心问题。Richardson外推extrapolation。

S是辛普森公式，T是梯形公式。
Romberg龙贝格
推导细节在后面。



近似程度更好的原因是只考虑截断误差，不考虑舍入误差。二者的区别
假设导数相等，公式推导不难。

下面是计算次序。

下面还是比较重要的。


就是π

利用公式$|I-T_m^{(k)}|<|T_m^{(k)}-T_m^{(k-1)}|/(4^m-1)$

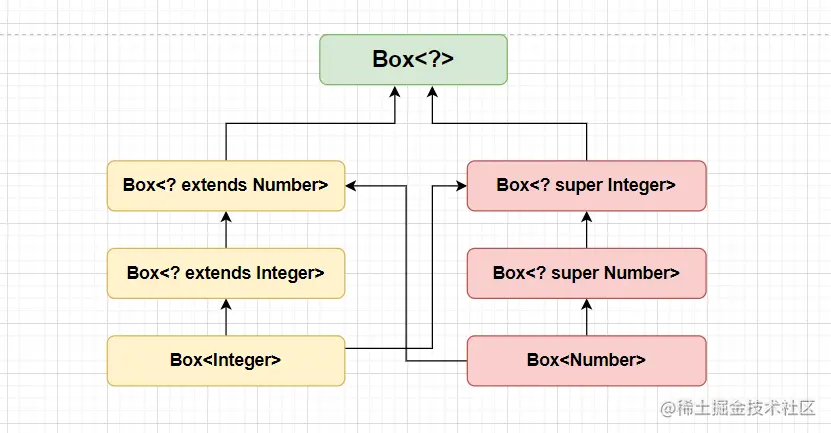
五、高斯求积公式

1.一般理论(1定义1例题)

2n+1是代数精度，n是A_k的个数。
依据上面的公式带入即可。


这个注不用管。

2.构造高斯求积公式方法（二）【定理加证明】

先确定了节点 x_k ，后利用方程组求解系数A_k 。

此证明是考试的最高难度！
充分性和必要性
这里H_n是次数不超过n次的多项式集合。看书52页

5、Gauss型求积公式

5.1Gauss型求积公式的一般理论【2定理1例题】

去掉了x₀

书31页公式3.5：

和书61页：

？？这个内积是怎么变为积分的。看第3章【逼近与拟合】的3.内积与内积空间

此处$\rho (x)=x^2$
l(x)是拉格朗日的基函数。

5.2多种Gauss型求积公式

与书122页的略有不同。不同的是n。书上从0开始，

这里换元改变的积分上下界。 求积公式和误差都变了,Simpson细节可以看上节第4章第一部分【数值积分（数值微分）】

t_i对应x_i回到区间0-1.，只要积分区间是[-1,1]就行
Simpson的结果是什么？

书上第n=5有一行有问题。0.1039919745改为：0.0103991975
书124页。125页例题12重要。

知识结构图（需要注意有例题的部分）

最后的作业：