0098 蓝桥杯真题01

import java.util.Calendar;

/*
* 世纪末的星期
* 曾有邪教称1999年12月31日是世界末日。当然该谣言已经不攻自破。还有人称今后的某个世纪末的12月31日，如果是星期一则会…
* 有趣的是，任何一个世纪末的年份的12月31日都不可能是星期一!! 于是，“谣言制造商”又修改为星期日…
* 1999年的12月31日是星期五，请问：未来哪一个离我们最近的一个世纪末年（即xx99年）的12月31日正好是星期天（即星期日）？
* 请回答该年份（只写这个4位整数，不要写12月31等多余信息）
*
* 思路
* 运用日期API中Calendar类
*
* 构造方法
* 1.protected Calendar() :由于修饰符是protected，所以无法直接创建该对象。需要通过别的途径生成该对象
*
* 成员方法
* 1.static Calendar getInstance(): 使用默认时区和区域设置获取日历。通过该方法生成Calendar对象。
*                             如Calendar cr=Calendar.getInstance()；
* 2.public void set(int year,int month,int date,int hourofday,int minute,int second)
*    设置日历的年、月、日、时、分、秒。
*
* 3.public int get(int field):返回给定日历字段的值。所谓字段就是年、月、日等等。
*
* 日历字段
* 1.YEAR   年
* 2.MINUTE 分
* 3.DAY_OF_WEEK_IN_MONTH 某月中第几周
* 4.MONTH 月
* 5.SECOND/MILLISECOND 秒/毫秒
* 6.WEEK_OF_MONTH 日历式的第几周
* 7.DATE 日
* 8.DAY_OF_MONTH   日
* 9.DAY_OF_YEAR   一年的第多少天
* 10.HOUR_OF_DAY   时
* 11.DAY_OF_WEEK   周几
* 12.WEEK_OF_YEAR   一年的第多少周
*/
public class _01世纪末的星期 {
   public static void main(String[] args) {
       Calendar calendar = Calendar.getInstance();
       for(int i = 1999;i < 10000;i += 100) {
           calendar.set(Calendar.YEAR, i);//1999年
           calendar.set(Calendar.MONTH, 11);//从0开始，11为12月
           calendar.set(Calendar.DAY_OF_MONTH, 31);//31日
           if (calendar.get(Calendar.DAY_OF_WEEK) == 1){//星期天为1，星期一为2....
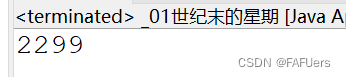
               System.out.println(i);
               break;//2299
           }
       }
   }
}

/*
* 小明参加了学校的趣味运动会，其中的一个项目是：跳格子。
* 地上画着一些格子，每个格子里写一个字，如下所示：
* 从我做起振
* 我做起振兴
* 做起振兴中
* 起振兴中华
* 比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。
* 要求跳过的路线刚好构成“从我做起振兴中华”这句话。
* 请你帮助小明算一算他一共有多少种可能的跳跃路线呢？
*
* 思路
* 枚举：递归和迭代
* 递归三要素
* 1.找重复，利用重复不断减小问题的规模；
* 2.找变化，变化的状态量就是递归的参数；
* 3.找出口，判断什么可以退出递归。
*
* 观察题目，其实在每个格子上时都只能向下走或者向右走，在当前格子上有两种走法，
* 而当到达边界处时，比如走到最下面一行格子或者最右边一列格子时，只能一路向右或向下走，这时从当前格子走到最后只能有一种走法。
*/
public class _02振兴中华 {
   public static void main(String[] args) {
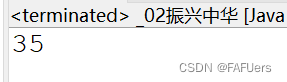
       int ans = f(0, 0);
       System.out.println(ans);//35
   }

   private static int f(int x, int y) {//变化（坐标在变）
       if (x == 3||y == 4) {//出口（走到边界只有1种走法）
           return 1;
       }
       return f(x + 1, y) + f(x, y + 1);//重复（没有走到边界，有两种走法，相加）
   }
}

import java.math.BigInteger;

/*
* 梅森素数如果一个数字的所有真因子之和等于自身，则称它为“完全数”或“完美数”
* 例如：6 = 1 + 2 + 3
* 28 = 1 + 2 + 4 + 7 + 14
* 早在公元前300多年，欧几里得就给出了判定完全数的定理：
* 若 2^n - 1 是素数，则 2^(n-1) * (2^n - 1) 是完全数。
* 其中 ^ 表示“乘方”运算，乘方的优先级比四则运算高，例如：2^3 = 8， 2 * 2^3 = 16, 2^3-1 = 7
* 但人们很快发现，当n很大时，判定一个大数是否为素数到今天也依然是个难题。
* 因为法国数学家梅森的猜想，我们习惯上把形如：2^n - 1 的素数称为：梅森素数。
* 截止2013年2月，一共只找到了48个梅森素数。新近找到的梅森素数太大，以至于难于用一般的编程思路窥其全貌，所以我们把任务的难度降低一点：
* 1963年，美国伊利诺伊大学为了纪念他们找到的第23个梅森素数 n=11213，在每个寄出的信封上都印上了“2^11213-1 是素数”的字样。
* 2^11213 - 1 这个数字已经很大(有3000多位)，请你编程求出这个素数的十进制表示的最后100位。
*
* 思路
* 运用API中的BigInteger类
* 在Java中提供了用于大数字运算的类，即 java.math.BigInteger 类和 java.math.BigDecimal 类。
* 这两个类用于高精度计算，其中BigInteger 类是针对整型大数字的处理类，而 BigDecimal 类是针对大小数的处理类。
*
* 1.java.math.BigInteger.valueOf(long value)方法
* 返回一个BigInteger，其值等于作为参数传递的long的值。
* 该方法是静态方法，因此不需要使用此方法创建BigInteger类的对象。
* 我们可以通过BigInteger.valueOf(long value)代码调用此函数。
*
* 2.基本运算
* 返回值为BigInteger类型
* add()       加
* subtract()   减
* multiply()   乘
* divide()       除
* mod()       取模
* remainder()   求余
* pow()       平方
* abs()       绝对值
* negate()       相反数
*
* 3.比较大小
* compareTo()返回一个int型数据：1 大于； 0 等于； -1 小于
* max()，min()：分别返回大的（小的）那个BigInteger数据
*
* 4.常量
* ZERO，ONE，TEN 返回值为BigInteger类型
*
* 5.字符串方法
* public String substring(int beginIndex)
* public String substring(int beginIndex, int endIndex)
* beginIndex -- 起始索引（包括）, 索引从 0 开始。
* endIndex -- 结束索引（不包括）。
*/
public class _03梅森素数 {
   public static void main(String[] args) {
       BigInteger x = BigInteger.valueOf(2).pow(11213).subtract(BigInteger.ONE);//2^11213-1
       String s = x.toString();//转为字符串
       int length = s.length();//长度
       String ans = s.substring(length - 100);//最后100位
       System.out.println("最后" + ans.length() + "位是" + ans);//输出
       //8586718527586602439602335283513944980064327030278104224144971883680541689784796267391476087696392191
   }
}

/*
* 小李的店里专卖其它店中下架的样品电视机，可称为：样品电视专卖店
* 其标价都是4位数字（即千元不等）。
* 小李为了标价清晰、方便，使用了预制的类似数码管的标价签，只要用颜色笔涂数字就可以了
* 这种价牌有个特点，对一些数字，倒过来看也是合理的数字。如：1 2 5 6 8 9 0都可以。
* 这样一来，如果牌子挂倒了，有可能完全变成了另一个价格，比如：1958 倒着挂就是：8561，差了几千元啊!!
* 当然，多数情况不能倒读，比如，1110 就不能倒过来，因为0不能作为开始数字。
* 有一天，悲剧终于发生了。某个店员不小心把店里的某两个价格牌给挂倒了。并且这两个价格牌的电视机都卖出去了!
* 庆幸的是价格出入不大，其中一个价牌赔了2百多，另一个价牌却赚了8百多，综合起来，反而多赚了558元。
* 请根据这些信息计算：赔钱的那个价牌正确的价格应该是多少？
*
* 思路
* 1.枚举四位数，简单筛选
* 2.将其颠倒，和原价做差
* 3.将赔2百多的放入一个集合，将赚8百多的放入一个集合
* 4.遍历两个集合，检查是否相加为558
*
* 相关方法
* 1.contains() 方法用于判断字符串中是否包含指定的字符或字符串
* 2.continue 语句是跳过循环体中剩余的语句而强制执行下一次循环，其作用为结束本次循环
* 3.parseInt() 方法用于将字符串参数作为有符号的十进制整数进行解析
* 4.charAt() 方法用于返回指定索引处的字符。索引范围为从 0 到 length() - 1
*/

import java.util.ArrayList;

public class _04颠倒的价牌 {
   public static void main(String[] args) {
       //创建集合，保存原价与差价
       ArrayList<Price> a1 = new ArrayList<>();
       ArrayList<Price> a2 = new ArrayList<>();

       //1.枚举四位数，简单筛选
       for(int i = 1000;i < 10000;i++) {
           String s = i + "";//转为字符串
           3,4,7不能颠倒，直接结束本次循环
           if (s.contains("3") || s.contains("4") || s.contains("7")) {
               continue;
           }
           //2.将其颠倒，和原价做差
           String res = reverse(s);//颠倒原价
           int i1 = Integer.parseInt(res);//转为int
           int minus = i1 - i;//颠倒价-原价
           //3.将赔2百多的放入一个集合，将赚8百多的放入一个集合
           if (minus < -200 && minus > -300) {//赔了2百多
               a1.add(new Price(i, minus));
           }
           if (minus < 900 && minus > 800) {//赚了8百多
               a2.add(new Price(i, minus));
           }
       }

       //遍历两个集合，检查是否相加为558
       for (Price price1 : a1) {
           for (Price price2 : a2) {
               if (price1.minus + price2.minus == 558) {//多赚558元
                   System.out.println("原价=" + price1.p + " 颠倒价-原价=" + price1.minus);
                   System.out.println("原价=" + price2.p + " 颠倒价-原价=" + price2.minus);
                   //答案为9088
               }
           }
       }
   }

   //编写reverse方法，实现颠倒原价
   private static String reverse(String s) {
       //创建一个大小为s.length的字符数组
       char[] chars = new char[s.length()];
       //遍历，j作为索引，将颠倒的价格保存在字符数组中
       for(int i = s.length() - 1,j = 0;i >= 0;i--,j++) {
           char c = s.charAt(i);
           //6颠倒成9，9颠倒成6，其他数字颠倒不变
           if (c == '6') {
               chars[j] = '9';
           }else if (c == '9') {
               chars[j] = '6';
           }else {
               chars[j] = c;
           }
       }
       //返回
       return new String(chars);
   }

   private static class Price{
       int p;//原价
       int minus;//颠倒价-原价
       //构造器
       public Price(int p, int minus) {
           this.p = p;
           this.minus = minus;
       }
   }
}

/*
* 三部排序
* 一般的排序有许多经典算法，如快速排序、希尔排序等。
* 但实际应用时，经常会或多或少有一些特殊的要求。我们没必要套用那些经典算法，可以根据实际情况建立更好的解法。
* 比如，对一个整型数组中的数字进行分类排序：
* 使得负数都靠左端，正数都靠右端，0在中部。注意问题的特点是：负数区域和正数区域内并不要求有序。可以利用这个特点通过1次线性扫描就结束战斗!!
* 以下的程序实现了该目标。
static void sort(int[] x)
{
   int p = 0;
   int left = 0;
   int right = x.length-1;

   while(p<=right){
   if(x[p]<0){
   int t = x[left];
   x[left] = x[p];
   x[p] = t;
   left++;
   p++;
   }
   else if(x[p]>0){
   int t = x[right];
   x[right] = x[p];
   x[p] = t;
   right--;
   }
   else{
   --------------------//填空
   }
   }
}
* 如果给定数组：
* 25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0
* 则排序后为：
* -3,-2,-16,-5,0,0,0,21,19,33,25,16,18,25
*/
public class _05三部排序 {
   static void sort(int[] x)
   {
       int p = 0;
       int left = 0;
       int right = x.length-1;

       while(p<=right){
       if(x[p]<0){//元素小于0，将元素和left位置元素交换，left,p后移
       int t = x[left];
       x[left] = x[p];
       x[p] = t;
       left++;
       p++;
       }
       else if(x[p]>0){//元素大于0，将元素和right位置元素交换，right前移
       int t = x[right];
       x[right] = x[p];
       x[p] = t;
       right--;
       }else{//元素等于0,不交换，直接让p后移
           p++;
       }
       }
   }
   //验证
   public static void main(String[] args) {
       int[] arr = {25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0};
       sort(arr);
       for (int i : arr) {
           System.out.print(i + " ");//-3 -2 -16 -5 0 0 0 21 19 33 25 16 18 25
       }
   }
}