本文为学习笔记

参考书籍：《深度学习入门 : 基于Python的理论与实现 》/ (日) 斋藤康毅著 ; 陆宇杰译. – 北京 : 人民邮电出版社, 2018.7（2019.5重印）、

文章中带文字的图片（如：图3-4）均来自书籍内容。

从感知机到神经网络

激活函数

前面文章中深度学习基础-感知机的函数的表示：
$$y=\{\begin{array}{r}0,(b+w_1{x}_1+w_2{x}_2\le 0)\\ 1,(b+w_1{x}_1+w_2{x}_2>0)\end{array}\text{\hspace{1em}(3.1)}$$
将式子（3.1）用一个函数$h(x)$来表示这种分情况的动作:
$$y=h(b+w_1{x}_1+w_2{x}_2)\text{\hspace{1em}(3.2)}$$

$$h(x)=\{\begin{array}{r}0,(x\le 0)\\ 1,(x>0)\end{array}\text{\hspace{1em}(3.3)}$$

$h(x)$函数一般称为激活函数，其作用在于如何来激活输入信号的总和。

式（3.2）的两个阶段：

1. 计算输入信号的加权总和
2. 激活函数转换这一总和

式（3.2）可以拆分：
$$a=b+w_1{x}_1+w_2{x}_2\text{\hspace{1em}(3.4)}$$

$$y=h(a)\text{\hspace{1em}(3.5)}$$

在图中表示：

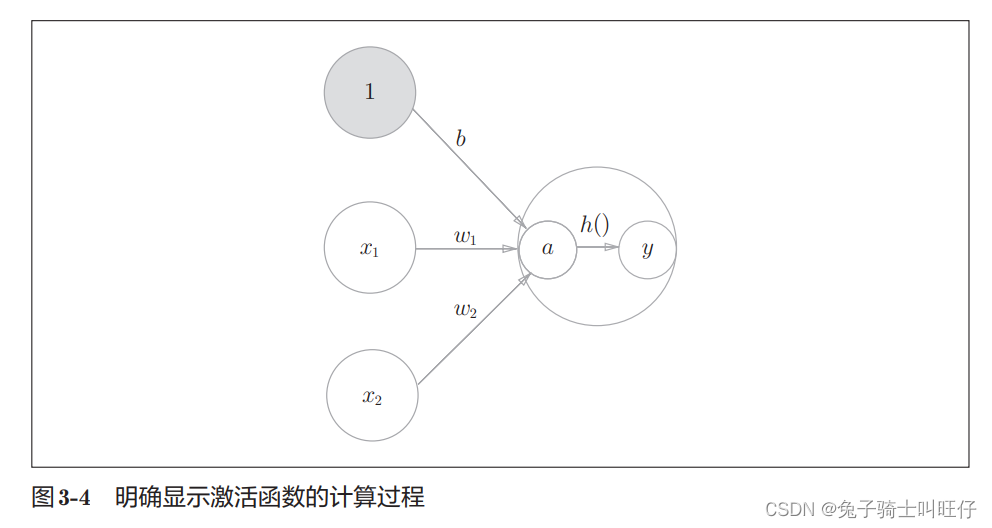
信号的加权总和为节点a，然后节点a被激活函数$h()$转换为节点$y$。

阶跃函数（感知机的激活函数）

$$h(x)=\{\begin{array}{r}0,(x\le 0)\\ 1,(x>0)\end{array}\text{\hspace{1em}(3.3)}$$

式子（3.3）表示的激活函数以阈值为界，一旦输入超过阈值，就切换输出。这样的函数称为阶跃函数。

阶跃函数实现：

import numpy as np


def step_function(x):
    """阶跃函数"""
    y = x > 0  # 如果传入NumPy数组x，y会是一个布尔型的数组
    return y.astype(np.int)  # astype()方法转换NumPy数组的类型，将y数组中的布尔值转为int型


demo = np.array([1, -1, 3])
# y = demo > 0  # [ True False  True]
# print(y)
result = step_function(demo)
print(result)  # [1 0 1]

阶跃函数绘制：

import numpy as np
import matplotlib.pyplot as plt


def step_function2(arr):
    """阶跃函数"""
    return np.array(arr > 0, dtype=np.int)  # 直接判断传入的形参大小并转换为int型的结果：0或1


x = np.arange(-5.0, 5.0, 0.1)  # 从-5.0到5.0每隔0.1取一个值
y = step_function2(x)  # 将x数组传入阶跃函数，每个值对应的结果保存在y数组

plt.plot(x, y)  # 绘制(x, y)函数图像
plt.title("Step function")  # 图的名称
plt.xlabel("x")  # 横轴名称
plt.ylabel("y")  # 纵轴名称
plt.ylim(-0.1, 1.1)  # 纵轴的范围
plt.show()  # 展示图像

运行结果：

阶跃函数以0为界，输出从0切换到1，呈阶梯式变化。

sigmoid函数

$$h(x)=\frac{1}{1+e^{-x}}\text{\hspace{1em}(3.6)}$$

代码实现：

import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    """sigmoid激活函数"""
    return 1 / (1 + np.exp(-x))


demo = np.arange(-5.0, 5.0, 0.1)
result = sigmoid(demo)

plt.plot(demo, result)
plt.title("Sigmoid")
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(-0.1, 1.1)
plt.show()

运行结果：

阶跃函数和sigmoid函数绘制和对比

import numpy as np
import matplotlib.pyplot as plt
from sigmoid import sigmoid


def step_function2(arr):
    """阶跃函数"""
    return np.array(arr > 0, dtype=np.int)  # 直接判断传入的形参大小并转换为int型的结果：0或1


x = np.arange(-5.0, 5.0, 0.1)  # 从-5.0到5.0每隔0.1取一个值
y = step_function2(x)  # 将x数组传入阶跃函数，每个值对应的结果保存在y数组
y1 = sigmoid(x)

plt.plot(x, y, label="step")  # 绘制(x, y)step函数图像
plt.plot(x, y1, linestyle="--", label="sigmoid", )  # 绘制(x, y)sigmoid函数图像
plt.title("Step function & Sigmoid")  # 图的名称
plt.xlabel("x")  # 横轴名称
plt.ylabel("y")  # 纵轴名称
plt.ylim(-0.1, 1.1)  # 纵轴的范围
plt.legend()  # 设置图例的相关设置
plt.show()  # 展示图像

运行结果：

二者对比：

• 不同点：

  1. 平滑性不同，sigmoid是平滑曲线，输出随输入发生连续性变化；step是以0为界，输出发生急剧性变化。
  2. 返回值不同，sigmoid可以返回实数，0.731、0.456…；step只能返回0或者1。

• 相同点：

  1. 两者输入较小时接近0（为0），输入较大时接近1（为1）。

  2. 输出信号都在0和1之间。

  3. 二者均为非线性函数。

     线性函数：是一条笔直的直线

神经网络的激活函数必须使用非线性函数

神经网络的激活函数必须使用非线性函数

神经网络的激活函数必须使用非线性函数

ReLU函数

ReLU: Rectified Linear Unit

在输入大于0时，直接输出该值；在输入小于等于0时，输出0。

公式：
$$h(x)=\{\begin{array}{r}x,(x>0)\\ 0,(x\le 0)\end{array}\text{\hspace{1em}(3.7)}$$
代码实现：

import numpy as np
import matplotlib.pyplot as plt


def relu(x):
    """ReLU函数"""
    return np.maximum(0, x)  # maximum从输入的值中选较大的值输出


a = np.arange(-5.0, 5.0, 0.1)
y = relu(a)

"""绘图"""
plt.plot(a, y)
plt.title("ReLU")
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(-1.0, 5.0)
plt.show()

运行结果：