static_cast 无条件转换，静态类型转换

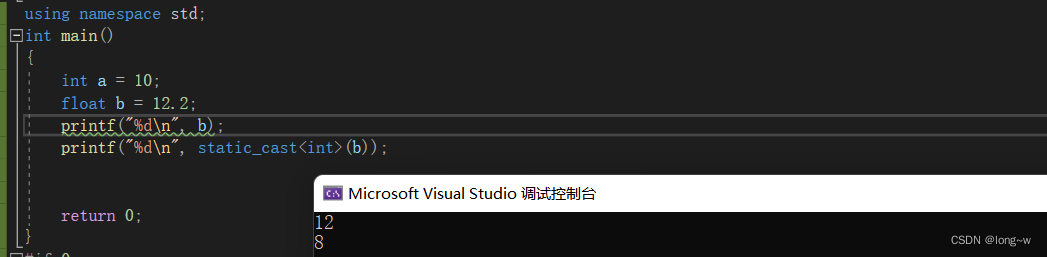
1.基本数据类型之间的转换
bool,char,short,int ,float,long,double

using namespace std;
int main()
{
	int a = 10;
	float b = 12.2;
	printf("%d\n", b);
	printf("%d\n", static_cast<int>(b));
	return 0;
}

2.枚举类型之间的转换

using namespace std;
int main()
{
	enum A { A1 = 1, A2 = 2 };
	enum B { B1 = 3, B2 = 4 };
	A a = A1;
	int c = 2;
	a = static_cast<enum A> (c);
	cout << a << endl;
}

不建议超出范围转换

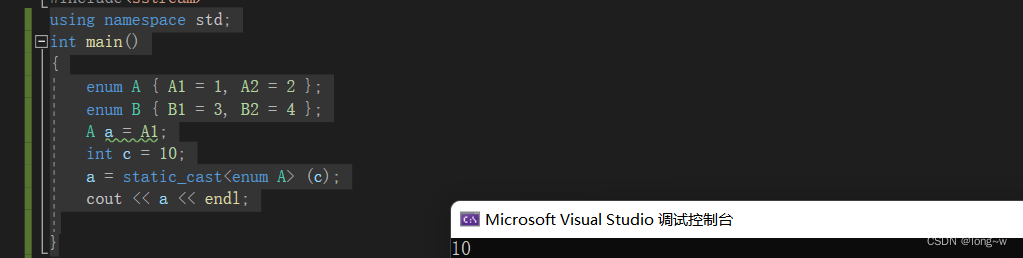
using namespace std;
int main()
{
	enum A { A1 = 1, A2 = 2,A3 = 3,A4 = 4 };
	enum B { B1 = 3, B2 = 4 };
	A a = A1;
	B b = B2;
	a = static_cast<enum A> (b);
	cout << a << endl;

}

3.指针之间的转换

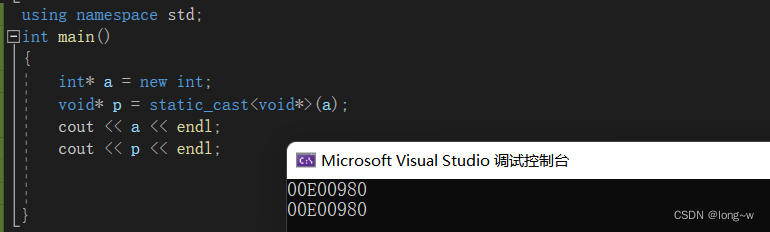
1.指针类型转void * , void * 再转换回原来的类型

using namespace std;
int main()
{
	int* a = new int;
	void* p = static_cast<void*>(a);
	cout << a << endl;
	cout << p << endl;


}

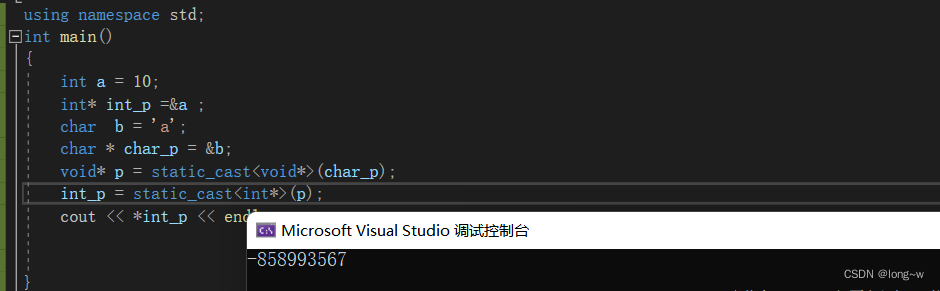
2.不同类型之间的指针的转换
直接转换是不允许的

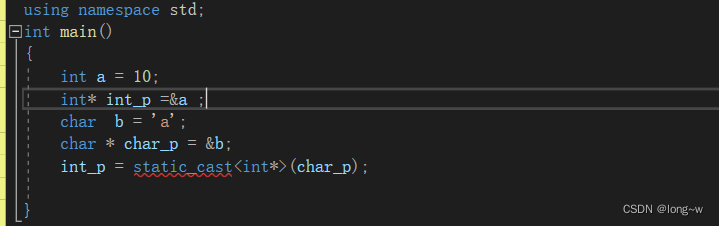
通过void * 作媒介是可以的，不过不安全


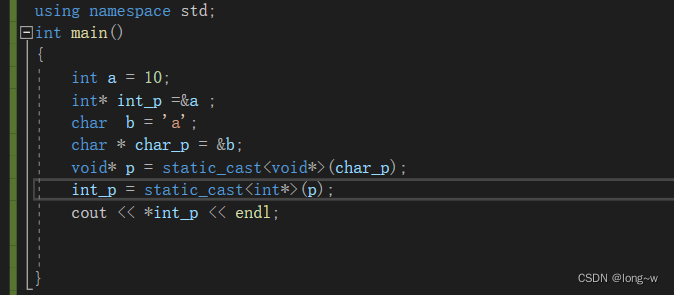
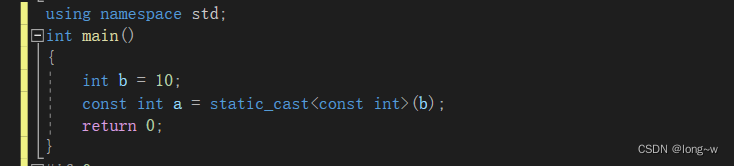
4.变量转换为常量

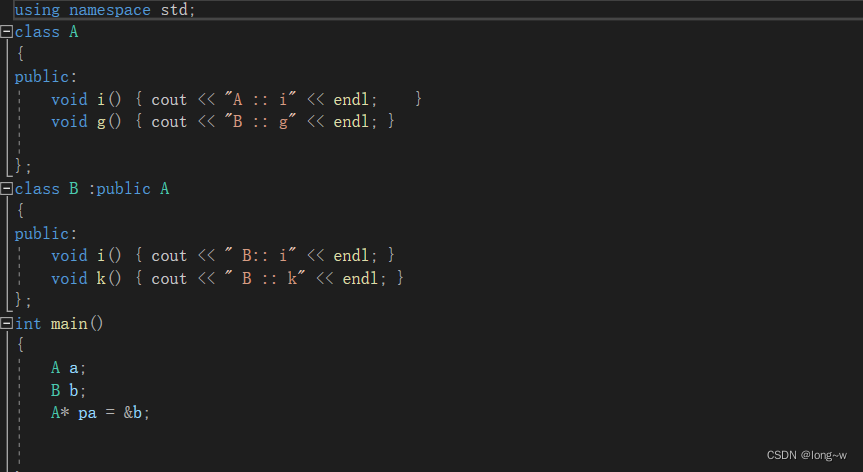
5.基类和派生类之间的转换

基类的指针指向派生类的对象的时候，派生类的对象的转换是隐式的

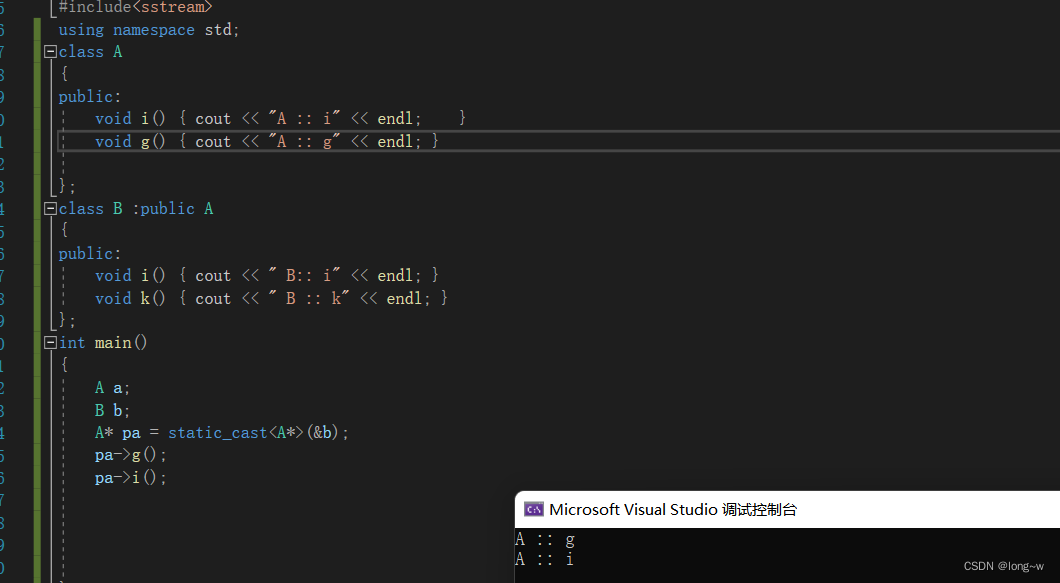
不过最好显式的写上，因为是基类的指针，所以调用的都是基类的函数

派生类的指针指向基类对象时，是不允许的

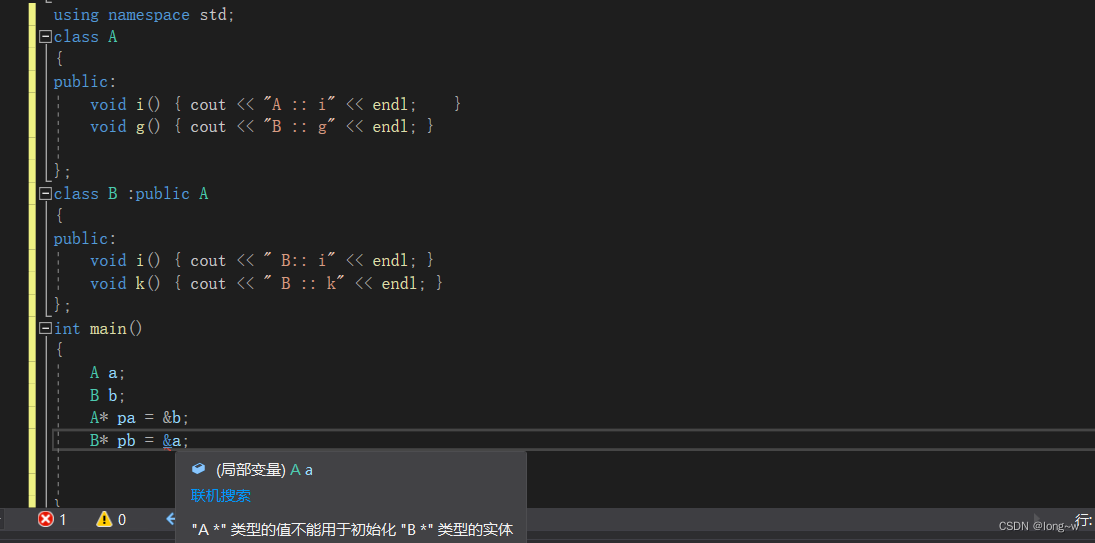
我们可以使用static_cast 进行转换

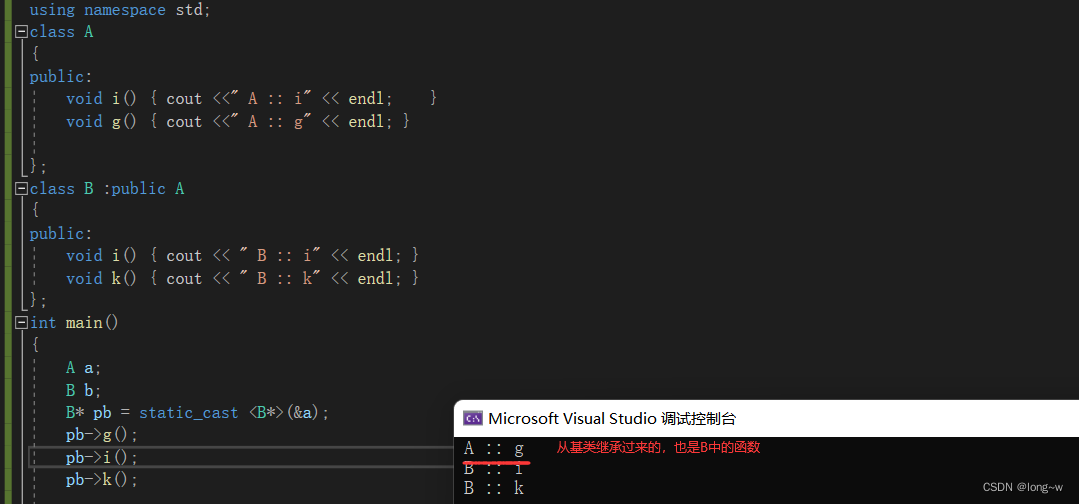
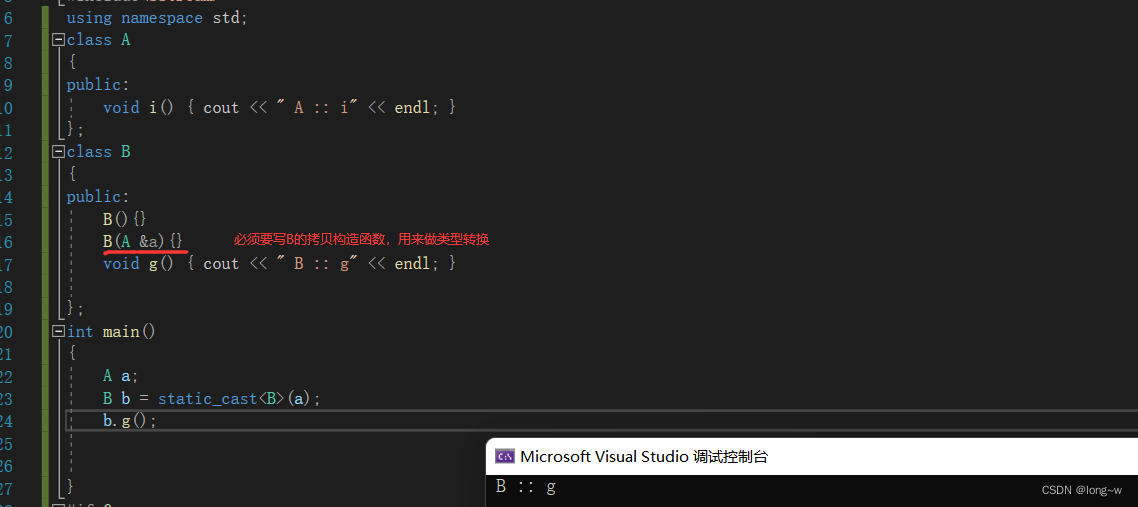
6.两个没有关系之间的类的转换

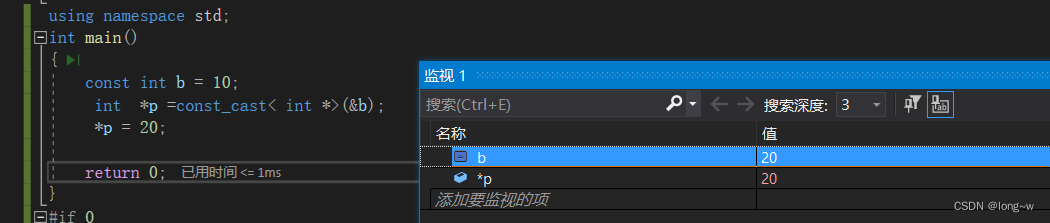
const_cast 去掉类型的const或volatile属性

去掉类型的const

去掉类型的volatile

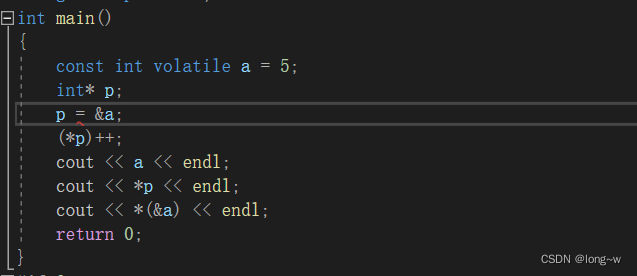
const int volatile a = 5;
	int* p;
	p = const_cast<int*>(&a);
	(*p)++;
	cout << a << endl;
	cout << *p << endl;
	cout << *(&a) << endl;
	return 0;

如果不使用const_cast的话，就会报错

dynamic_cast 有条件转换，动态类型转换，运行时检查类型安全（转换失败返回NULL）

dynamic_cast 动态转换 将基类的指针（必须是指向派生类对象的基类指针才能转化成功）安全的转换为派生类的指针或引用，并用派生类的指针或引用调用非虚函数
该类型要包含虚函数，才能转换

如下面所示，当把父类对象的地址转化给子类指针时，因为不安全，所以通过dynamic_cast一强转就为NULL。

class Base
{
public:
	virtual ~Base(){}
};
class Child :public Base
{
	~Child(){}
};
int main()
{
	Base* b = new Base();
	Child* c1 = static_cast<Child*> (b);
	Child* c2 = dynamic_cast<Child*>(b);//为NULL

	Base* b2 = new Child();
	Child* c3 = static_cast<Child*> (b2);
	Child* c4 = dynamic_cast<Child*>(b2);

	return 0;
}

reinterpret_cast 仅重新解释类型，但没有进行二进制的转换

reiterpret_cast 指针转换为另外一种指针，不修改指针变量存储格式，重新解释指针类型，也可以将指针转换为整型值

using namespace std;
int main()
{
	float ff = 3.4f;
	float* pf = &ff;
	int* pi = reinterpret_cast<int*>(pf);
	cout << *pi << endl;
	cout << *pf << endl;
	long j = reinterpret_cast<long>(pi);
	cout << j << endl;

}