Numpy

NumPy （ Numerical Python 的简称）是高性能科学计算和数据分析的基础包，

其中包含了数组对象 ( 向量、矩阵、图像等 ) 以及线性代数等。

NumPy库主要功能

• ndarray( 数组 ) 是具有矢量算术运算和复杂广播能力的多维数组。

• 具有用于对数组数据进行快速运算的标准数学函数。

• 具有用于读写磁盘数据、操作内存映射文件的工具。

• 具有线性代数、随机数生成以及傅里叶变换功能。

• 具有用于集成由 C 、 C++ 、 Fortran 等语言编写的代码的工具。

NumPy库的安装

CMD

# 打开命令窗口

• pip install numpy # 在 cmd 中输入

NumPy库的调用

import numpy as np #约定俗成

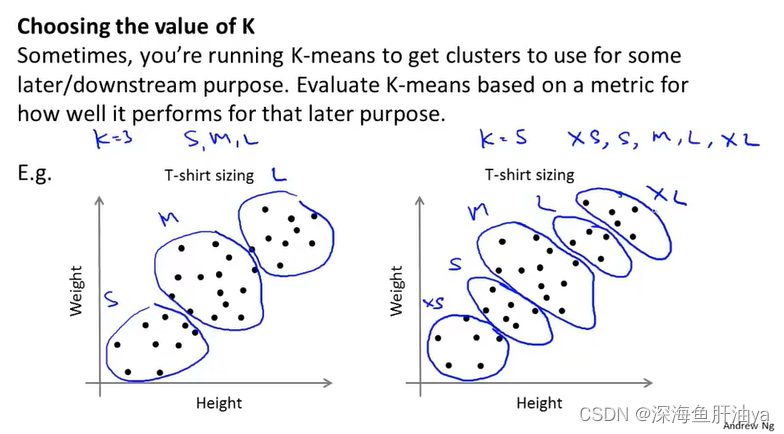
数据维度的理解

二维数据

二维数据由多个一维数据构成，是一维数据的组合形式。

表格是典型的二维数据。

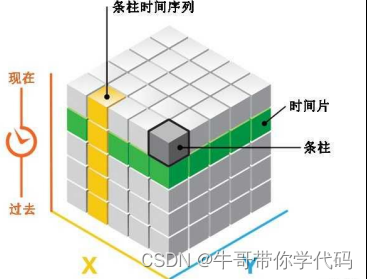
多维数据

多维数据由一维或二维数据在新维度上扩展形成。（比如在二维数据基础上加上时间轴）

一维数据：列表和集合类型一维数据：列表和集合类型

[3.13, 4.13, 2,34] 有序

{3.13, 4.13, 2,34} 无序

二维数据：列表类型

多维数据：列表类型

高维数据：字典类型或数据表示格式

举例：

计算 A 2 +B 3 ，其中， A 和 B 是一维数组。

a=[0,1,2,3,4]

b=[5,6,7,8,9]

c=[]

for i in range(0,5):

c.append(a[i]**2+b[i]**3)

import numpy as np

a_array=np.array(a)

b_array=np.array(b)

c=a_array**2+b_array**3

数组优势

数组对象可以去掉元素间运算所需的循环，使一维向量更像单个数据

设置专门的数组对象，经过优化，可以提升这类应用的运算速度

观察：科学计算中，一个维度所有数据的类型往往相同

数组对象采用相同的数据类型，有助于节省运算和存储空间

数组

NumPy 库处理的最基础数据类型是由同种元

素构成的多维数组 (ndarry) ，简称“数组”。

• numpy 数组的维数称为秩，每一个线性的数组称为轴。

• 同一个 numpy 数组中所有元素的类型一般是相同的。

例子

ndarray 在程序中的别名是： array.

np.array() 输出成 [] 形式，元素由空格分割 .

>>> import numpy as np
>>> a=[[1,2],[3,4]]
>>> a_array=np.array(a)
>>> a_array
array([[1, 2],
[3, 4]])
>>> type(a_array)
numpy.ndarray

数组创建

从 Python 中的列表、元组等类型创建 ndarray 数组

使用 NumPy 中函数创建 ndarray 数组，如： arange ,ones, zeros 等。

从字节流（ raw bytes ）中创建 ndarray 数组。

从文件中读取特定格式，创建 ndarray 数组。

内置数据结构创建数组

基本格式： NumPy 将根据数据情况关联一个 dtype 类型

np.array(list/tuple, dtype=np.float32)

例子

>>> np.array([[1,2],[3,4]])
>>> np.array(((1,2),(3,4)))
array([[1, 2],
[3, 4]])

有整数有浮点数则转浮点

>>> np.array([[1,1.1],(2,2.1)])
array([[1. , 1.1],
[2. , 2.1]])

数组元素的类型

dtype( 数据类型 ) 是一个特殊对象，它含有 ndarry 将一块内存解释为特定数 据类型所需要的信息。

数组元素的类型：原因解释

ndarray 为什么要支持这么多种元素类型？

Python语法仅支持整数、浮点数和复数 3 种类型

Ndarry 的优势

• 科学计算涉及数据较多，对存储和性能都有较高要求

• 对元素类型精细定义，有助于 NumPy 合理使用存储空间并优化性能

• 对元素类型精细定义，有助于程序员对程序规模有合理评估

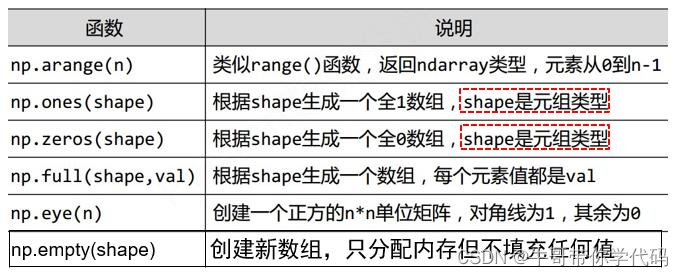
常用创建数组的函数

使用 Numpy 中函数创建 ndarry 数组，如 arrange ， ones ， zeros 等

实例

>>> np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

>>> np.ones((3,6))
array([[1., 1., 1., 1., 1., 1.],
      [1., 1., 1., 1., 1., 1.],
      [1., 1., 1., 1., 1., 1.]])

>>> np.ones((2,4),dtype=np.int32) :
array([[1, 1, 1, 1],
      [1, 1, 1, 1]])

>>> np.eye(4)
array([[1., 0., 0., 0.],
      [0., 1., 0., 0.],
      [0., 0., 1., 0.],
      [0., 0., 0., 1.]])
    
>>> np.full((2,4),4)
array([[4, 4, 4, 4],
[4, 4, 4, 4]])

已知尺度大小创建数组

使用 NumPy 中函数创建 ndarray 数组，如： arange, ones, zeros 等

数组对象的属性

a = np.array([[0, 1, 2, 3], [4, 5, 6, 7]]) #二维数组
b = np.array([0, 1, 2, 3]) #一维数组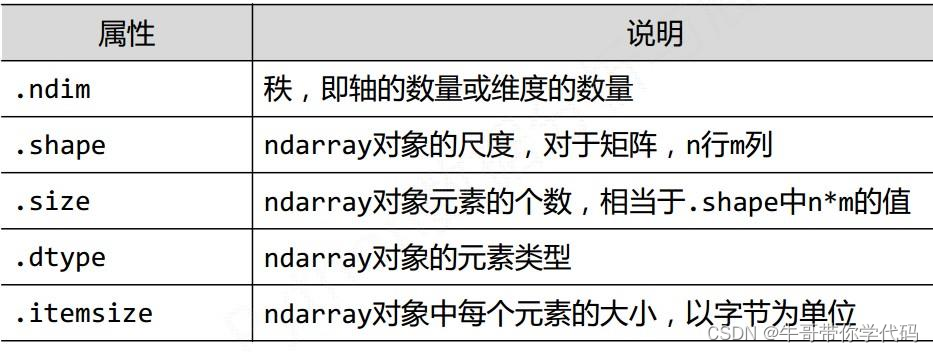

维度的改变

对于创建后的ndarray数组，可以对其进行维度变换和元素类型变换。

下方的输入为数组

>>> a = np.ones((2,3,4), dtype=np.int32)
>>> a.reshape((3,8))
array([[1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1]])
>>> a #a的内容改变
array([[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]],
[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]]])

>>> a.flatten() #平铺
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1])
>>> aa=np.arange(8).reshape((2,4))
array([[0, 1, 2, 3],
[4, 5, 6, 7]])
In [27]: aa.transpose() #转置
array([[0, 4],
[1, 5],
[2, 6],
[3, 7]])

#不确定数目
>>> a.reshape((4,-1))
array([[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]])

一维数组转换为列表

数组转换为列表

array.tolist()

>>> np.arange(8).reshape((2,4))
array([[0, 1, 2, 3],
[4, 5, 6, 7]])

>>> np.arange(8).reshape((2,4)).tolist()
Out[42]: [[0, 1, 2, 3], [4, 5, 6, 7]

二维数组：轴的概念

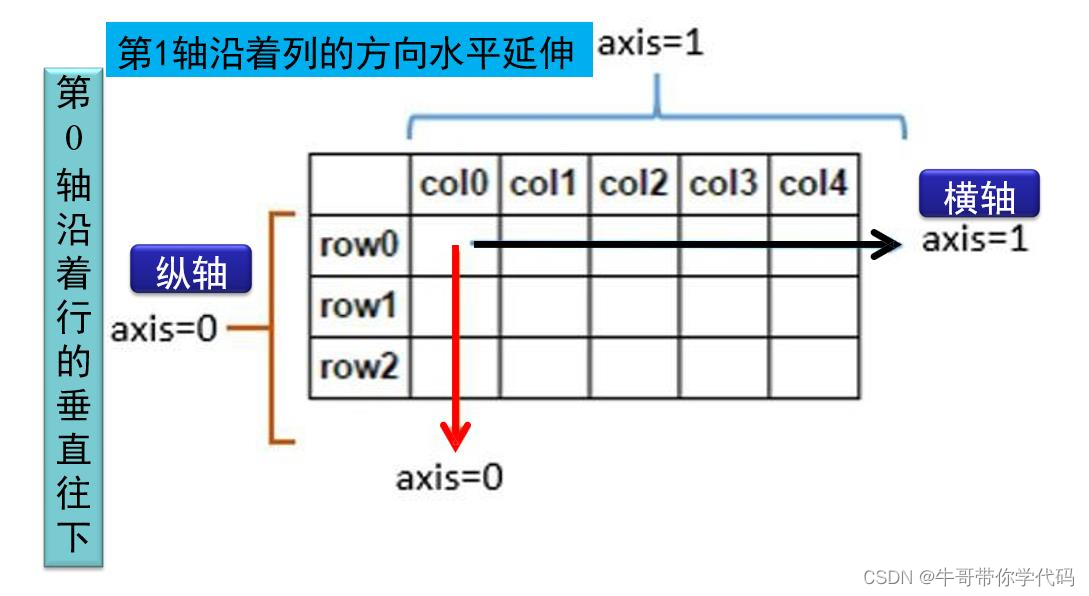
二维数组：组合操作

二维数组：分割操作

>>> a=np.arange(9).reshape((3,3))
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]]
>>> b=np.split(a, 3, axis=1)
[array([[0],
[3],
[6]]),
array([[1],
[4],
[7]]),
array([[2],
[5],
[8]])]

数组的索引

一维数组的基本索引

一维数组索引与 Python 的列表类似

格式：array_name[索引值或序列]

• 索引值0 开始从左递增，或 -1 开始从右递减

• 起始编号 : 终止编号 ( 不含 ): 步长， 3 元素冒号分割

>>> a=np.arange(1,6)
>>> a
array([1, 2, 3, 4, 5])

## 单个索引，切片索引
>>> a[2]
3
>>> a[1:4:2]
array([2, 4])

## 索引值为序列
>>> a[1,3] #列表
array([2, 4])
>>> a[np.array([1,3])] #数组
array([2, 4])

可变对象——数组

数组是一个可变对象

>>> a=np.arange(1,6)
>>> b=a
>>> b[-1]=8
>>> b
array([1, 2, 3, 4, 8])
>>> a
array([1, 2, 3, 4, 8])
>>> b=a[:]
>>> b[-1]=8
>>> b
array([1, 2, 3, 4, 8])
>>> a
array([1, 2, 3, 4, 8])

数组切片与视图

数组切片是原始数组的视图，数据不会被复制，视图上的任何修改都会直接反映到源数组。

>>> a=np.arange(1,6)
>>> b=a[1:3]
>>> b[-1]=8
>>> b
array([2, 8])
>>> a
array([1, 2, 8, 4, 5])

>>> b=a[1:3].copy()
>>> b[-1]=8
>>> a
array([1, 2, 8, 4, 5]) # 保持不变

二维数组的基本索引

轴 0 索引值，轴 1 索引值。

行索引值、列索引值与一维数组相同。

ndarry [axis0_index,axis1_index]

>>> arr2d =np.arange(9).reshape(3,3)
>>> arr2d
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> arr2d[1,2]
5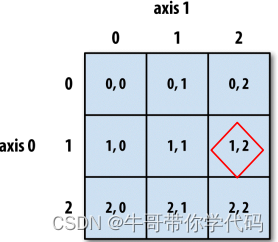

二维数组的切片索引

二维数组默认沿着第 0 轴（即行索引）切片的。切片是沿着一个轴向选取元素的。

ndarry[axis0_slice, axis1_slice]

>>> arr2d =np.arange(9).reshape(3,3)
>>> arr2d
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
>>> arr2d[:2] #默认行索引
array([[0, 1, 2],
[3, 4, 5]])

>>> arr2d[:2, : ] #：表示所有元素
array([[0, 1, 2],
[3, 4, 5]])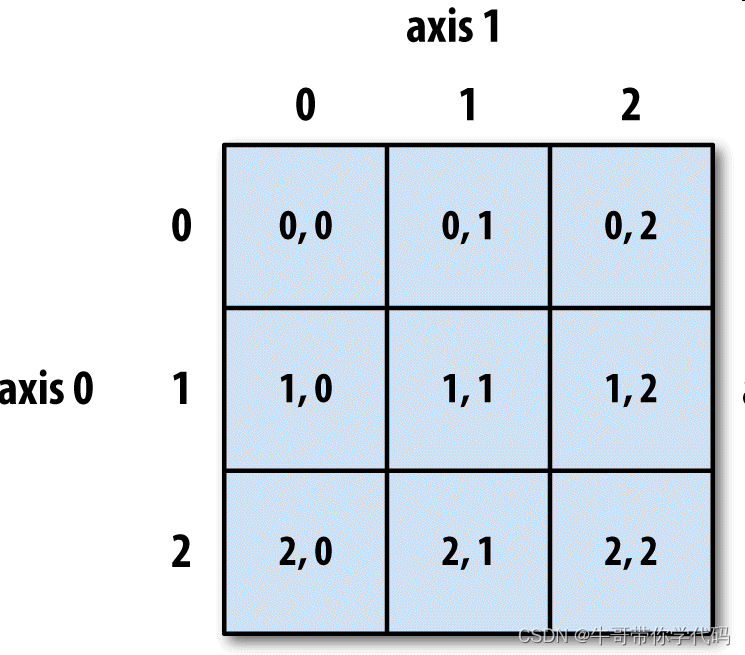

二维数组的切片索引实例

二维数组增删改查操作

实例

>>> np.insert(a,1,[0,0,0,0],0) #增加
array([[ 0,1, 2,3],
[0,0,0,0],
[4,5,6,7],
[8,9,10,11]])

>>> np.delete(a,0,1) #删除含有0的列
array([[ 1,2,3],
[ 5,6,7],
[ 9, 10, 11]])

>>> np.append(a, [[1,2,3,4]], 0)
#末尾修改
array([[ 0,1, 2,3],
[ 4,5,6,7],
[ 8,9,10,11],
[ 1,2,3,4]]) :

>>> np.where(a==1)#查找含有1的
(array([0], dtype=int64),
array([1], dtype=int64))

数组的矢量化

矢量化 (vectorization) ：数组不用编写循环即可实现对数据执行批量运算。

大小相等的数组之间的任何算数运算都将应用至元素级。

数组与标量之间的运算作用于数组的每一个元素

>>> a=np.arange(1,9).reshape((2,4))
>>> a
array([[1, 2, 3, 4],
[5, 6, 7, 8]])

>>> a**2
array([[ 1, 4, 9, 16],
[25, 36, 49, 64]], dtype=int32)
>>> 1/a
array([[1, 0.5, 0.333333,0.25],
[0.2 ,0.166667, 0.14285, 0.125])

布尔型索引

假设每个名字都对应 data 数组中的一行，而我们想要选出对应于名字 “Bob” 的所有行。

布尔型数组的长度必须跟被索引的轴长度一致。

布尔型索引：切边索引数组直接赋值

切片索引 ( 整数型或布尔型 ) 后的数组均可直接赋值

>>> data = np.random.randn(7, 4)
>>> a
array([[-1.04067731, -0.03879518, 0.98019589, -0.88795274],
[-1.18705612, 0.4635102 , 0.91812337, -0.81458408],
[ 0.86988195, 0.3959186 , 0.33063004, -0.1769584 ],
[-0.46452414, -0.46827261, -0.20851302, 0.22864186],
[-0.04973137, -0.23765974, 0.54263156, -0.06470696],
[-0.89274831, 2.5559152 , 1.02892789, 2.16099481],
[ 2.07400286, -1.96976106, -0.97007937, 1.84897368]])
array([[ True, True, False, True], [ True, False, False, True], [False,
False, False, True],
[ True, True, True, False], [ True, True, False, True], [ True, False,
False, False], [False, True, True, False]])

>>> idx=(data<0)
>>> data[data < 0] = 0
>>> data
array([[0., 0., 0.98019589, 0.],
[0., 0.4635102 , 0.91812337, 0.],
[0.86988195, 0.3959186 , 0.33063004, 0.],
[0., 0., 0., 0.22864186],
[0., 0., 0.54263156, 0.],
[0., 2.5559152 , 1.02892789, 2.16099481],
[2.07400286, 0., 0., 1.84897368]])

用于布尔型数组的方法

sum 经常被用来对布尔型数组中的 True 值计数。

any 用于测试数组中是否存在一个或多个 True 。

all 则检查数组中所有值是否都是 True 。

>>> arr = np.random.randn(10)
>>> arr
array([-0.71497659, -0.97902783, -
0.18698594, 0.08350516, -0.42339716,
-0.86465629, 0.70777104, -1.22436206, -
1.02389181, -1.30741898])
>>> arr_bool=(arr>=0)
array([False, False, False, True, False, False,
True, False, False, False])

>>> arr_bool.sum()
2 #大于0的个数
>>> arr_bool.any()
True #存在大于0
>>> arr_bool.all()
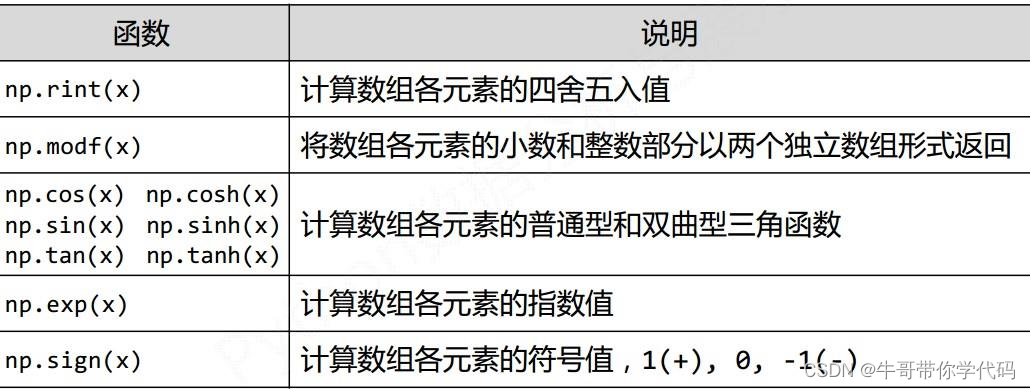
False #是否均大于0

一元算数函数

通用函数 (ufunc) 是一种对 ndarray 中的数据执行元素级运算的函数，可看作为简单函数的矢量化

函数。

对 ndarray 中的数据执行元素级运算的函数。

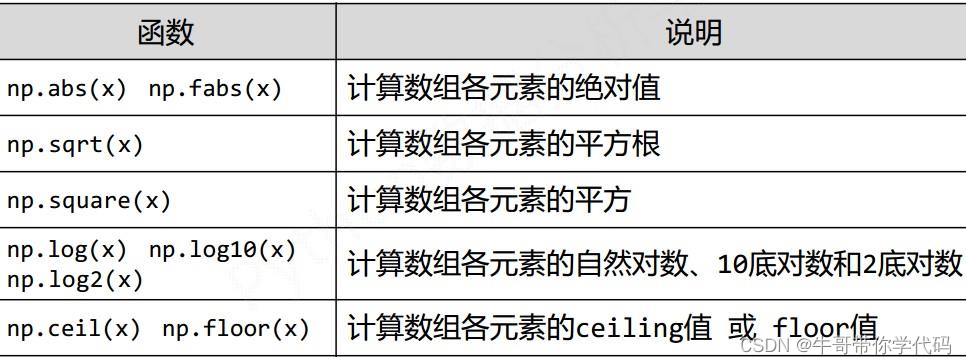
对ndarray中的数据执行元素级运算的函数

例子

>>> a=np.arange(1,10).reshape((3,3))
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> np.sqrt(a)
array([[1. , 1.41421356, 1.73205081],
[2. , 2.23606798, 2.44948974],
[2.64575131, 2.82842712, 3. ]])

>>> np.modf(b)
array([[0., 0.41421356, 0.73205081],
[0. , 0.23606798, 0.44948974],
[0.64575131, 0.82842712, 0. ]]),
array([[1., 1., 1.],[2., 2., 2.],[2., 2.,
3.]]))

二元算数函数

>>> np.nodf(b)
>>> a=np.arange(1,10).reshape((3,3))
>>> b=np.sqrt(a)
>>>np.fmax(a,b)
array([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])

>>> a>b
array([[False,True, True],
[ True, True, True],
[ True, True, True]])

meshgrid函数

适用于生成网格型数据，可以接受两个一维数组生成两个二维矩阵，对应两个数组中所有的 (x,y) 对。

xx,yy=np.meshgrid(x,y)

其中生成的第一个二维数组是以 xarray 为行，共 y-dimesion 行的向量；第二个二维数组是以

yarray 的转置为列，共 x-dimesion 列的向量。

>>> x=np.array([0,1,2,3]) #横坐标
>>> y=np.array([0,1,2,3,4]) #纵坐标
>>> xx,yy=np.meshgrid(x,y)

>>> xx
array([[0,1,2,3],
[0,1,2,3],
[0,1,2,3],
[0,1,2,3],
[0,1,2,3]])

>>> yy
array([[0,0,0,0],
[1,1,1,1],
[2,2,2,2],
[3,3,3,3],
[4,4,4,4])

三元函数——where函数

numpy.where 函数是三元表达式 x if condition else y 的矢量化版本

x if condition else y

||

V

np.where(condition,x,y)

>>> arr = np.random.randn(4,4)
>>> arr >0
array([[False, False, False, False],
[ True, True, False, True],
[ True, True, True, False],
[ True, False, True, True]],
dtype=bool)

>>> np.where(arr>0, 2,- 1)
array([[-2, -2, -2, -2],
[ 2, 2, -2 ,2],
[ 2, 2, 2 ,-2],
[ 2, -2, 2 ,2]])

集合逻辑

NumPy 提供了一些针对一维 ndarray 的基本集合运算，其中 np.unique 用于找出数组中的唯一值并

返回已排序的结果。

统计函数

通过数组上的一组数学函数对整个数组或某个轴向的数据进行统计计算。聚合计算（aggregation，通常叫做约简（reduction））

注意轴操作：axis=0或1

伪随机数的生成

numpy.random 模块对 Python 内置的 random 进行了补充，增加了一些用于高效生成多种概率分布

的样本值的函数。

Python 内置的 random 模块则只能一次生成一个样本值。

>>> from random import normalvariate
>>> N = 1000000
>>> samples = [normalvariate(0, 1) for _ in range(N)]
1.77 s +- 126 ms per loop (mean +- std. dev. of 7 runs, 1 loop each)
>>> np.random.normal(size=N)
61.7 ms +- 1.32 ms per loop (mean +- std. dev. of 7 runs, 10 loops each)

常用分布函数的随机数

线性代数

线性代数是任何数组库的重要组成部分， linalg 模块中有标准的矩阵分解运算以及诸如求逆和行列

式之类的函数

实例

专用函数

sort 函数返回排序后的数组

argsort 函数返回输入数组排序后的下标；

lexsort 函数根据键值的字典序进行排序；

• 例如： ind = np.lexsort((b,a)) # Sort by a, then by b

ndarray 类的 sort 方法可对数组进行原地排序；

msort 函数沿着第一个轴排序；

sort_complex 函数对复数按照先实部后虚部的顺序进行排序增强可维护性

Numpy文件操作

tofile() 和 fromfile()

• 数据以二进制格式写进文件，事先知道存入文件时数组的维度和元素类型。

save() 和 load()

• 用的二进制格式保存数据，它们会自动处理元素类型和形状等信息，以 .npy

或 .npz 为扩展名。

savetxt() 和 loadtxt()

• 读写 1 维和 2 维数组的文本文件。

np.loadtxt函数

np.loadtxt ( fname, dtype=<class 'float'>, comments='#', delimiter=None,

converters=None, skiprows=0, usecols=None, unpack=False, ndmin=0, encoding='bytes',

max_rows=None,*, like=None )

• fname

被读取的文件名（文件的相对地址或绝对地址）

• dtype

指定读取后数据的数据类型，例如 float32 ， int32 。

• comments 跳过文件中指定参数开头的行（即不读取）

• delimiter 指定读取文件中数据的分割符， ( 例如 ,csv 文件中的逗号 )

• skiprows

选择跳过的行数，默认从第一读取。 ( 例如 skiprows =1 ，从第二行开始读取 )

• converters 对读取的数据进行预处理

• usecols

指定仅读取的列

• unpack 选择是否将数据进行向量输出

• encoding 对读取的文件进行预编码。

>>> converters={1:_is_num}
#字典的形式，对指定 的列执行相关操作

读文件

np.loadtxt(frame,dtype=np.float, delimiter=None,unpack=False)

写文件

np.savetxt(frame, array, fmt='%.18e', delimiter=None)

总结

传送门：Python全套学习笔记

Python学习笔记（十六）——Numpy