序言

第三课这块要学习的几块知识如下：

在学完监督学习之后，接下来我们要学习的东西分别是聚类，异常检测，推荐系统和强化学习。

可以再回头看一眼这监督学习，非监督学习，强化学习的区别和联系：

https://hanhan.blog.csdn.net/article/details/127461500

一.什么是聚类

将开始介绍聚类算法。这将是一个激动人心的时刻，因为这是我们学习的第一个非监督学习算法。我们将要让计算机学习无标签数据，而不是此前的标签数据。

那么，什么是非监督学习呢？在课程的一开始，我曾简单的介绍过非监督学习，然而，我们还是有必要将其与监督学习做一下比较。

在一个典型的监督学习中，我们有一个有标签的训练集，我们的目标是找到能够区分正样本和负样本的决策边界，在这里的监督学习中，我们有一系列标签，我们需要据此拟合一个假设函数。与此不同的是，在非监督学习中，我们的数据没有附带任何标签，我们拿到的数据就是这样的：

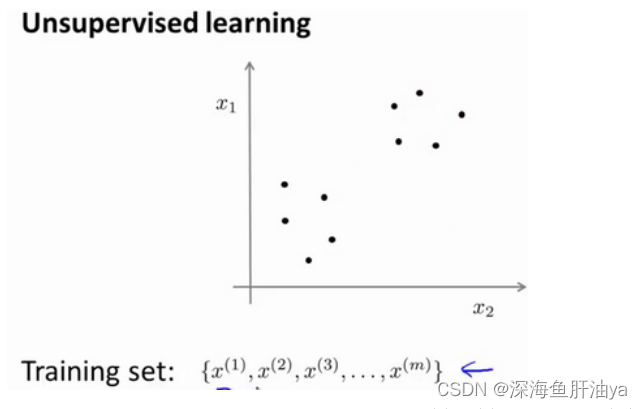
在这里我们有一系列点，却没有标签。因此，我们的训练集可以写成只有x1~xm。我们没有任何标签y。因此，图上画的这些点没有标签信息。也就是说，在非监督学习中，我们需要将一系列无标签的训练数据，输入到一个算法中，然后我们告诉这个算法，快去为我们找找这个数据的内在结构给定数据。我们可能需要某种算法帮助我们寻找一种结构。图上的数据看起来可以分成两个分开的点集（称为簇），一个能够找到我圈出的这些点集的算法，就被称为聚类算法。

这将是我们介绍的第一个非监督学习算法。当然，此后我们还将提到其他类型的非监督学习算法，它们可以为我们找到其他类型的结构或者其他的一些模式，而不只是簇。

我们将先介绍聚类算法。此后，我们将陆续介绍其他算法。那么聚类算法一般用来做什么呢？

在这门课程的早些时候，我曾经列举过一些应用：比如市场分割。也许你在数据库中存储了许多客户的信息，而你希望将他们分成不同的客户群，这样你可以对不同类型的客户分别销售产品或者分别提供更适合的服务。社交网络分析：事实上有许多研究人员正在研究这样一些内容，他们关注一群人，关注社交网络，例如Facebook，Google+，或者是其他的一些信息，比如说：你经常跟哪些人联系，而这些人又经常给哪些人发邮件，由此找到关系密切的人群。因此，这可能需要另一个聚类算法，你希望用它发现社交网络中关系密切的朋友。我有一个朋友正在研究这个问题，他希望使用聚类算法来更好的组织计算机集群，或者更好的管理数据中心。因为如果你知道数据中心中，那些计算机经常协作工作。那么，你可以重新分配资源，重新布局网络。由此优化数据中心，优化数据通信。

最后，我实际上还在研究如何利用聚类算法了解星系的形成。然后用这个知识，了解一些天文学上的细节问题。好的，这就是聚类算法。这将是我们介绍的第一个非监督学习算法。在下一个视频中，我们将开始介绍一个具体的聚类算法。

二.K-means算法

K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。

K-均值是一个迭代算法，假设我们想要将数据聚类成n个组，其方法为:

首先选择K个随机的点（注意这K个初始点的维度要和我们的训练示例维度相同，位置随机且要从所有的离散点中选K个，而不是自己指定三个原来没有的点），称为聚类中心（cluster centroids）；
对于数据集中的每一个数据，按照距离K个中心点的距离（即从K个质心当中找举例自己最近的那个），将其与距离最近的质心关联起来，即每个初始的簇质心都代表一个类，某个离散点离哪个质心最接近，这个离散点就属于这一类。
计算每一个组（即每一类的所有离散点）的平均值，将该类的质心移动到计算出的平均值点的位置，即新的质心点。
重复第二步和第三步，直到收敛（即再重复2，3步各距离什么的都不会变了，比如各离散点属于哪个类都已经不会再变动了）。

算法分为两个步骤，第一个for循环是赋值步骤，即：对于每一个样例，计算其应该属于的类。第二个for循环是聚类中心的移动，即：对于每一个类，重新计算该类的质心。

K-均值算法也可以很便利地用于将数据分为许多不同组，即使在没有非常明显区分的组群的情况下也可以。下图所示的数据集包含身高和体重两项特征构成的，利用K-均值算法将数据分为三类，用于帮助确定将要生产的T-恤衫的三种尺寸。

如果上面的讲解没看懂的话，可以看看下面的这个视频（随便上B站找个阅读量高的视频就ok了）：

k-means kmeans聚类算法清晰解释（带算例）_哔哩哔哩_bilibili

三.优化目标

这一节我们会提到K-means算法的成本函数（即它的目标优化函数，是的，它也有成本函数，数学真的很奇妙）了解它的成本函数一方面会帮助我们对程序进行调试修改，确保正确运行；另一方面

会在后面的视频中提到我们将通过它帮助K-means算法找到一个更好的簇，并且避免局部最优解。

符号：

c^(i)代表训练示例属于哪一个类（即类的序号）

u_k代表第k个聚类中心的位置

u_c(i)是x^(i)所属的那个簇的聚类中心

注：在K-means算法中K代表簇的数量，k代表聚类中心的下标（取值范围是1到k）

例如x^(i)被分配到第五个簇中，那么相应的c^(i)=5，u_c(i)=u_5

下图中的J即是成本函数，又叫失真函数，注意并不是x^(i)要和每个簇中心都要做相减取平方的操作，而是某个簇内的所有点要和自己这个簇的中心做相减取平方的操作，然后把每个点这般操作之后的差值之和做一个均值。K-means就是把这个均值函数的值降到越低越好，最后找到对应的c^(i)和u_k

四.初始化K-means

本来是在B站上看新版的视频，但是到了聚类这一块字幕翻译的实在可能不下去了，所以我只能转战网易公开课来看老版的了，字幕看着是真舒服。

吴老师刚上来一顿讲，其实就是随机选择。。。K-means算法最后的收敛状态取决于它的初始状态，所以最后收敛状态会随着初始簇质心的不同而不同，所以K均值算法可能会落到局部最优（local optima）内。

如下图，上方那个是全局最优，下面那俩都只是局部最优

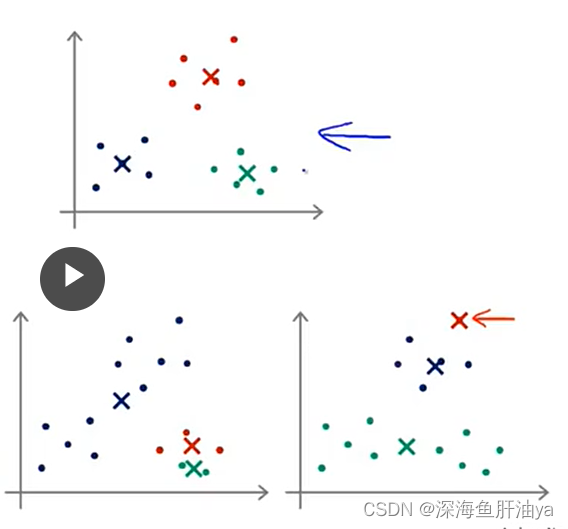
要尽量避免局部最优，一个可以采用的方法是进行多次随机初始值的选取，运行多次K-means算法，这样可以尽量去得到一个比较好的局部最优或全局最优。通常这样多次运行的次数在50到1000之间，如下图，运行100次，然后把这100次的成本函数值比较一下，选取其中最小的一个

当类的数量不多时（七八个），使用这种执行多次的方法效果很好，但是当类的数量很多时（成千上百个），多次执行的方法可能也不会有太大的改善，但是起码可以给算法一个合理的起点。

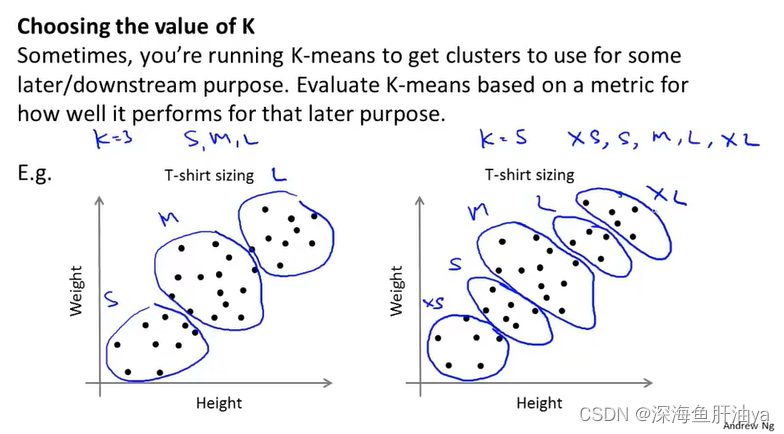
五.选择聚类数量（k=?）

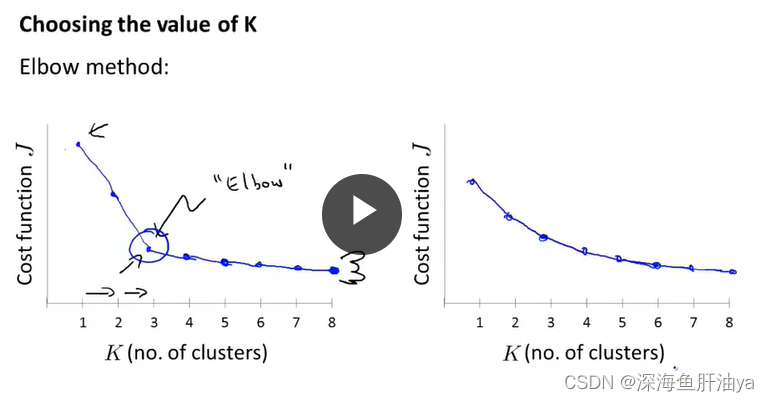
方法一：肘部法则

需要一个个试k值，横轴是k值，纵轴是成本函数值J，看到左侧的图，最开始k增加的时候，成本J下降的很快，但是当越过了某个点之后，J减小的就很慢了，这条曲线像我们的手肘弯起来了，所以叫肘部法则，即选取那个“肘部的点”，在左图中是k=3的点。但是通常我们实际情况下遇到的都是右边那个图，比较平滑，没有左边那个图拐弯拐的那么明显，所以不太好判断哪个是肘部点。

所以不能期望它解决这方面的任何问题。

方法二：实际意义

比如你现在用这个K-means算法是为了帮助你根据这些数据来分析你的T-shirt服装产品分别做出哪些尺寸，这就取决于一些实际意义。如下图，同样的数据，如果你认为服装的尺寸有S，M，L三种即可，那么初始化时让k=3，但是如果你认为顾客可能选择的尺寸是XS,S,M,L,XL的话，那么你就得另k=5了。