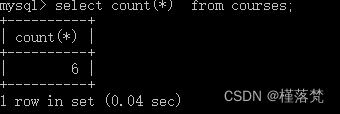
本帖子讨论图的基本概念,这一章,我们将利用有序对和二元关系的概念定义图。图分为了无向图和有向图,他们有共性也有区别,请大家注意体会,用联系和辩证的观点去认识。
1、无向图和有向图
注意无向图和有向图的表示,最大区别在于边的集合的表示,无向图中边集为无序集V&V的子集, 有向图中边集为有序集VXV的子集。
1)无向图
2)有向图

2、几类特殊的图
通常用 G表示无向图, D表示有向图,V(G)、 E(G)、V(D)、E(D)、分别是G和D的顶点集, 边集。
n 阶图: n个顶点的图
有限图: V, E都是有穷集合的图
零图: E=
空图: V=
平凡图: 一阶零图
简单图:既无平行边也无环的图.
n阶无向完全图Kn: 每个顶点都与其余顶点相邻的n阶无向简单图。边数m=n(n-1)/2, 出/入度=n-1
n阶有向完全图: 每对顶点之间均有两条方向相反的有向边的n阶有向简单图。边数m=n(n-1), D=d=2(n-1)。完全图举例如下: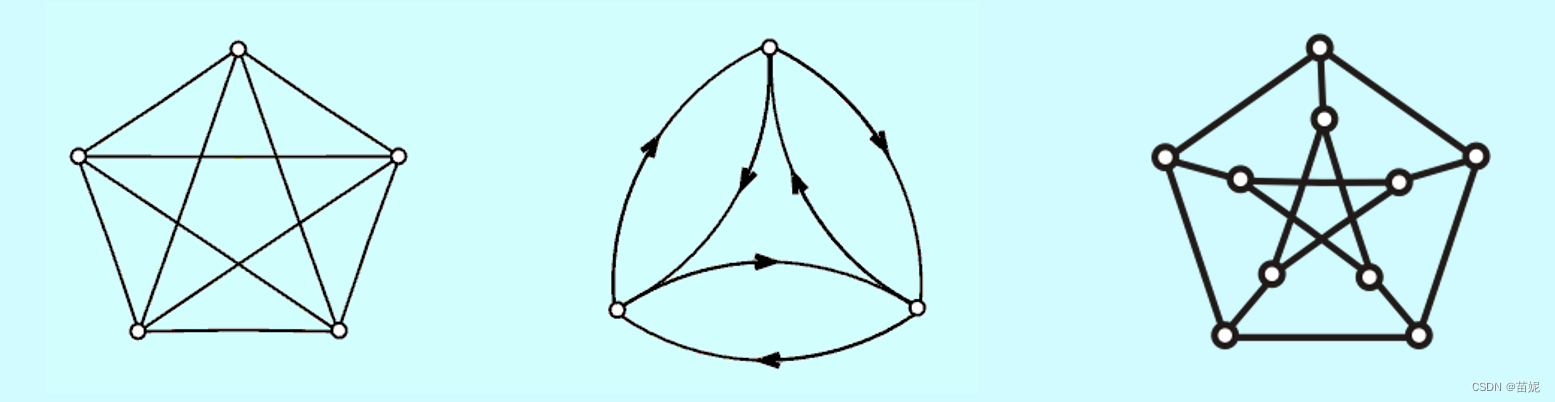
补图:设G=<V,E>为n阶无向简单图,以V为顶点集,所有使G成为完全图Kn的添加边组成的集合为边集的图,称为G的补图
3、图的度数
1)无向图顶点的度数

2)有向图顶点的度数
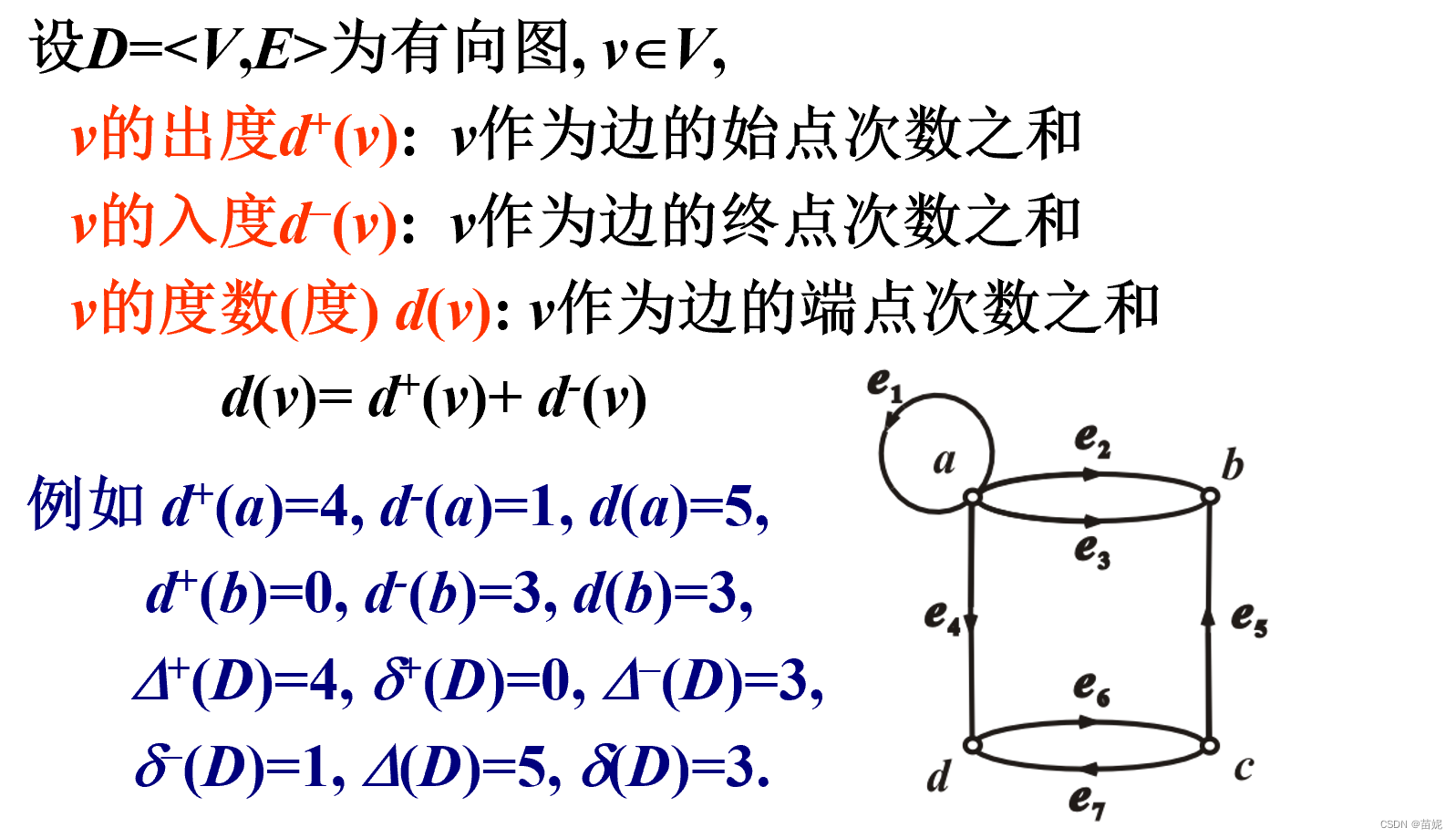
3)图的度数列

4、握手定理
1)握手定理
任意无向图和有向图的所有顶点度数之和都等于边数的2倍, 并且有向图的所有顶点入度之和等于出度之和等于边数。
2)握手定理推论
在任何无向图和有向图中,奇度顶点的个数必为偶数.
3)应用
 5、图的连通性
5、图的连通性
1)通路与回路
下面复杂的概念让人头晕,其实就是我们常规理解的能走的通的路,只不过是用数学语言表达出来了 ,将结点和与结点相邻的边连起来。

2)无向图的连通性
对于无向图中的任何两个结点都是有通路的,那么此图连通,即:

更进一步的,我们可以将连通关系,定义为等价关系,等价关系具有自反性,对称性,传递性。因为具有传递性必然连通。平凡图是一阶零图,它的关系矩阵表示,就是一个全1矩阵,因此也是连通图。
![]()
当我们对连通关系做等价划分的时候,有几个等价类,就有几个连通分支。

3)有向图的连通性
设有向图D=<V,E> ,u可达v: u到v有通路. 规定u到自身总是可达的,可达具有自反性和传递性。
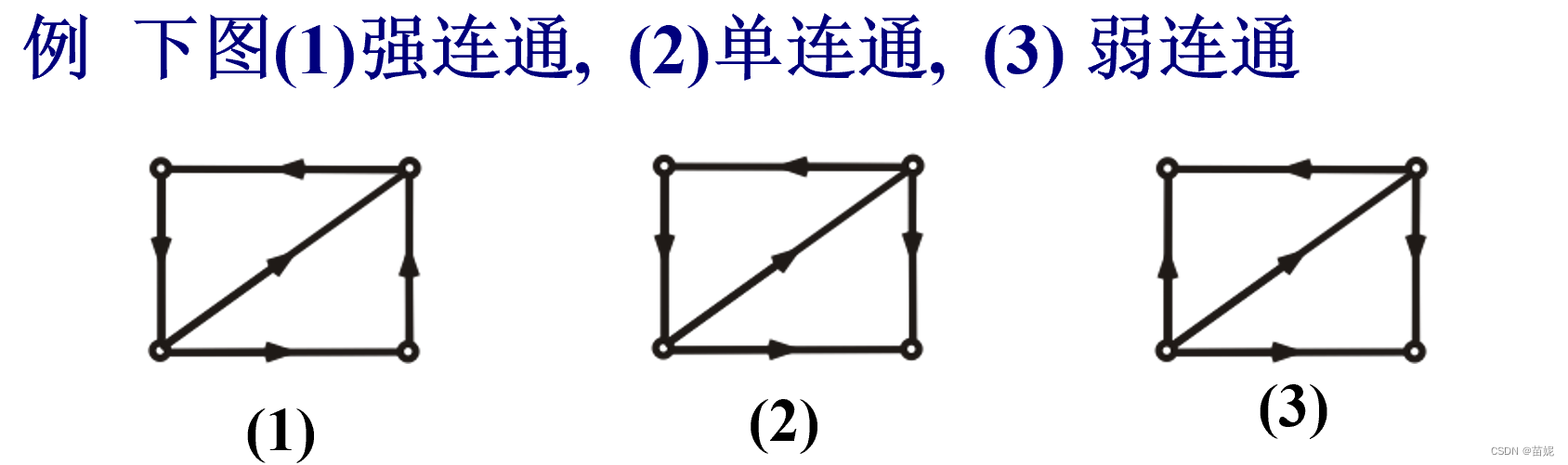
有向图的连通性包括了三种:
- D弱连通(连通): 基图为无向连通图
- D单向连通:
,u可达v 或v可达u
- D强连通:
,u与v相互可达
强连通单向连通
弱连通
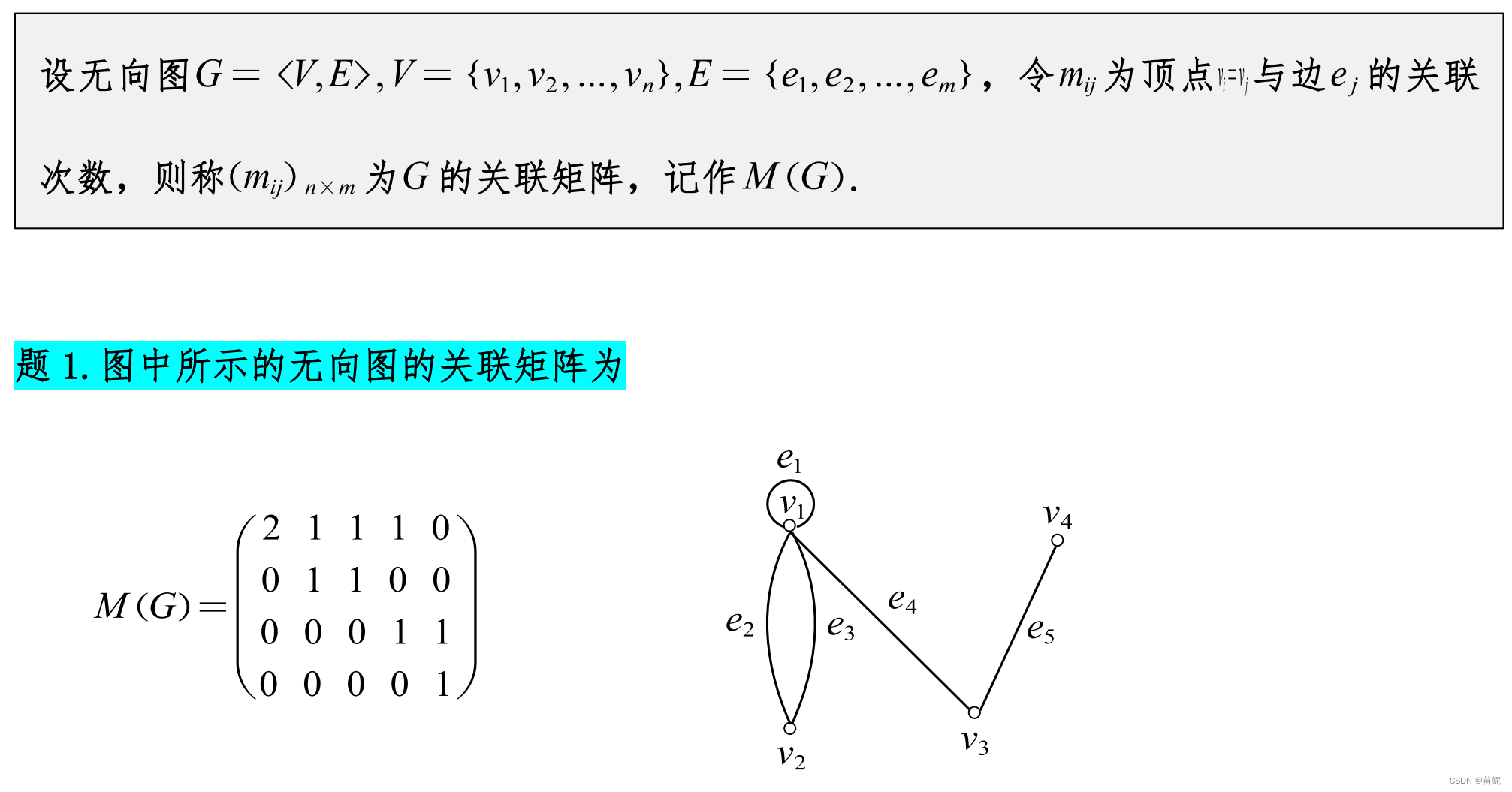
6、图的矩阵表示
图的矩阵表示,有三种方式:关联矩阵、邻接矩阵、可达矩阵。三者的区别在于,关联矩阵讨论的是顶点与边的关联次数、邻接矩阵讨论的是顶点之间的邻接边的条数、可达矩阵关注的是顶点之间是否可达,因此表达这些关系的矩阵尺寸是不同的,比如关注顶点与边之间的关系的矩阵,矩阵的行数就是顶点数,列数就是边数。
1)关联矩阵

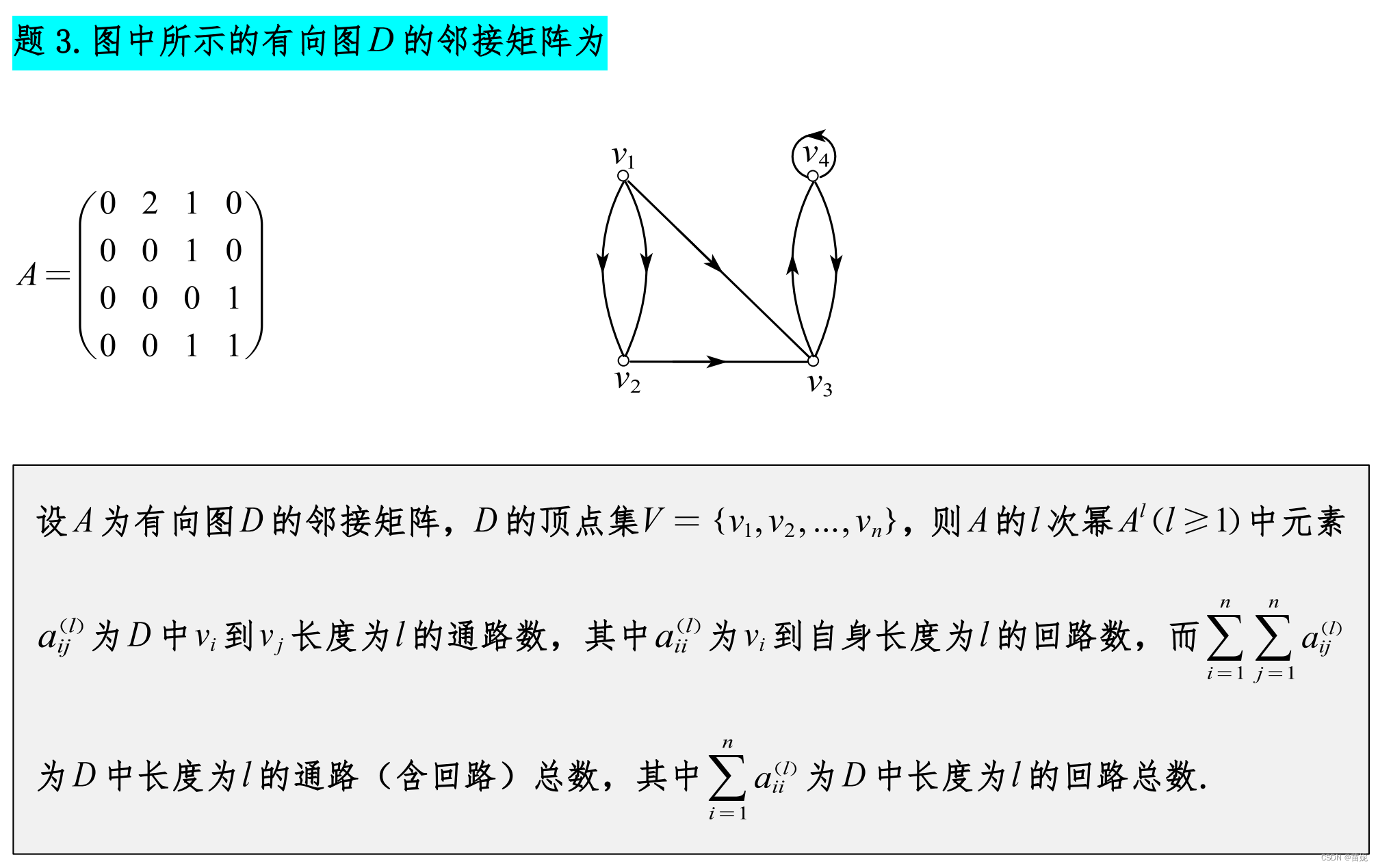
2)邻接矩阵


3)可达矩阵

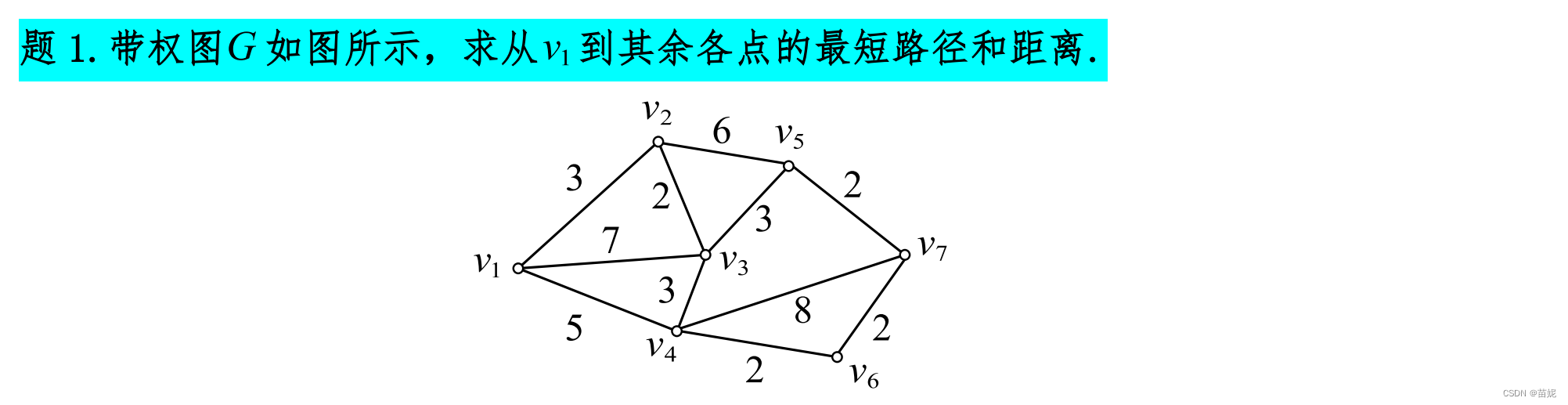
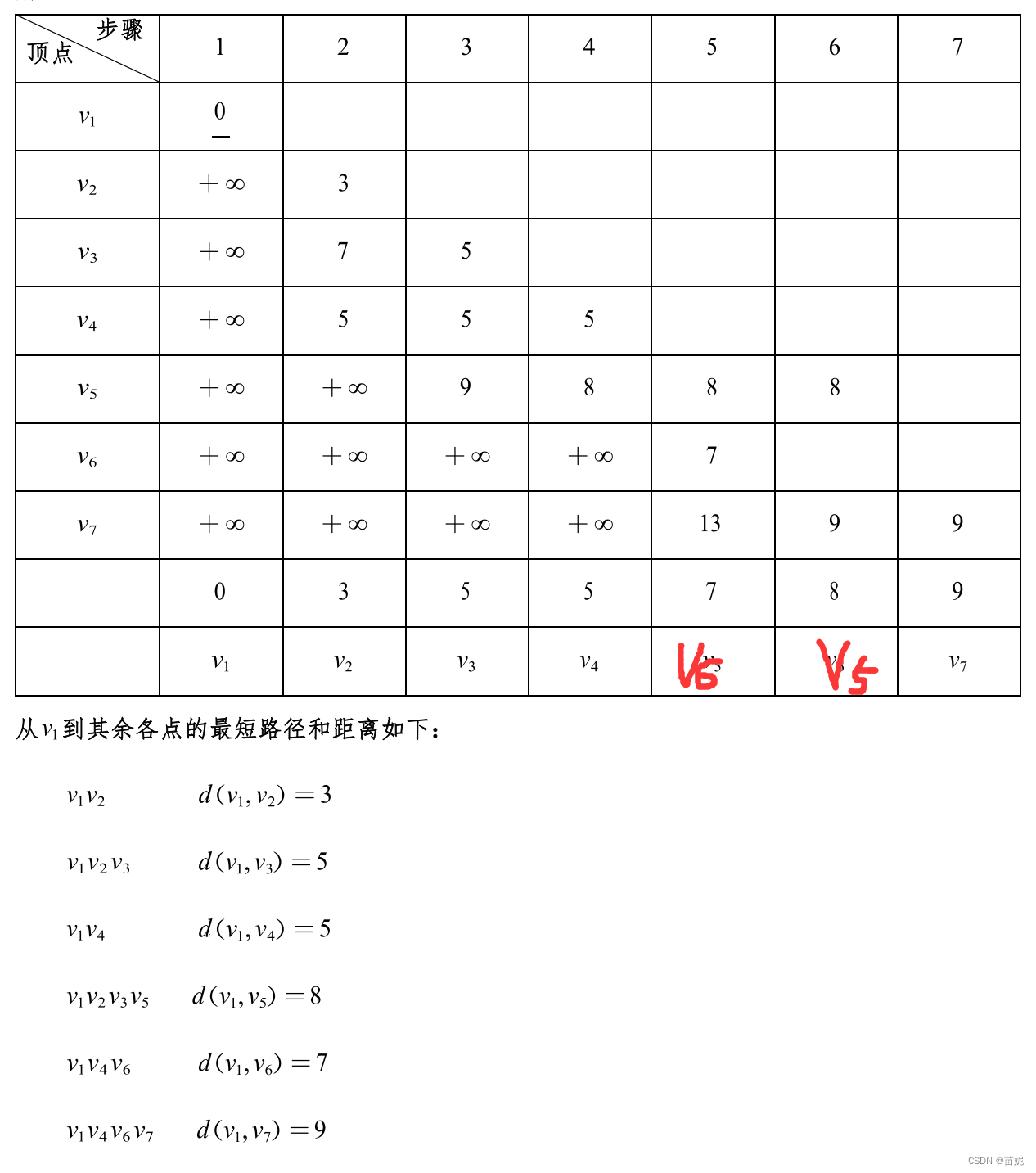
7、最短路径
我们把有向图的定义进行扩展,使得图不仅包含顶点集、边集、还包括边上的权值集合W,称为带权图。

给定两个顶点,我们用dijstra算法求解最短路径。dijstra算法是一种单源多目标的算法。