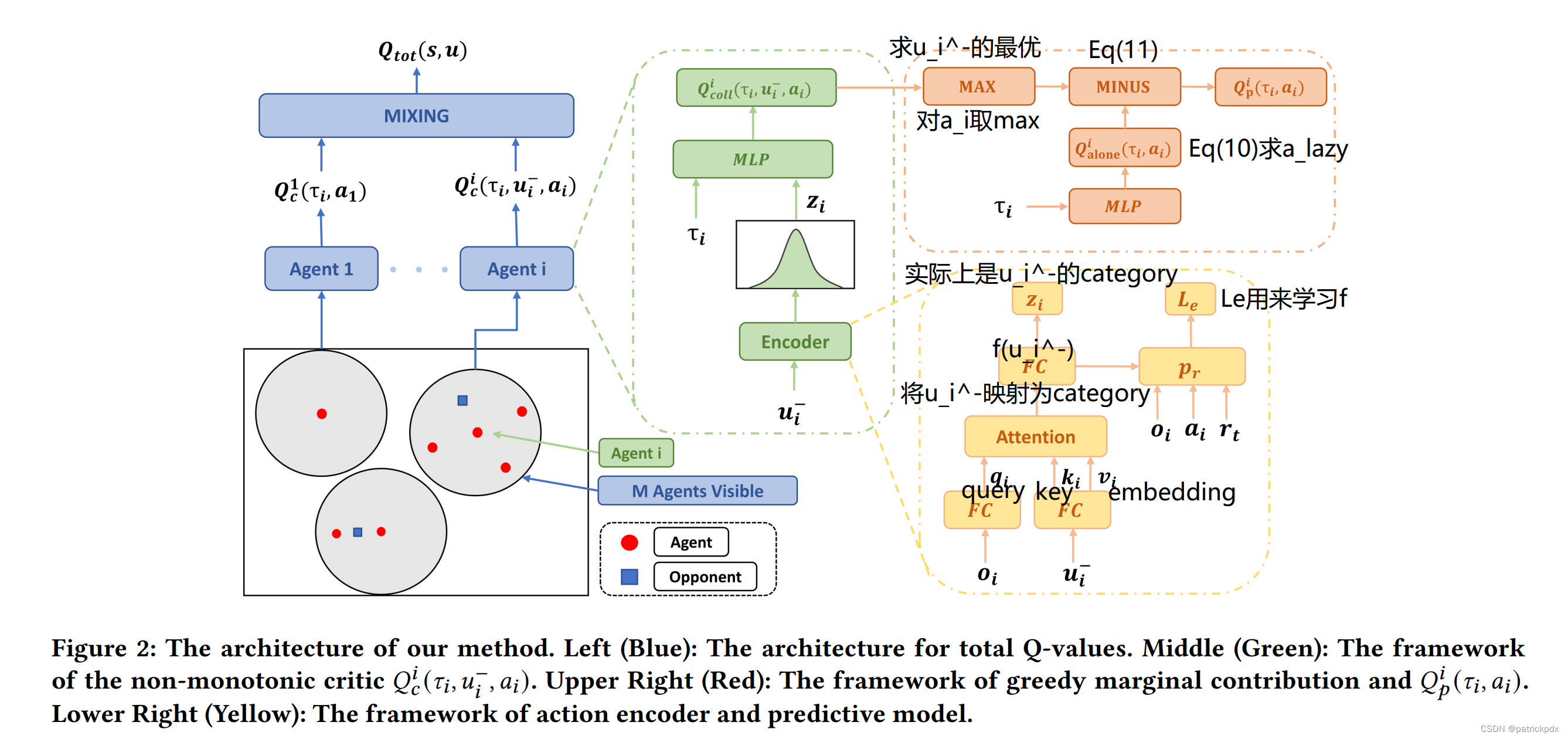
Adaptive Value Decomposition with Greedy Marginal Contribution Computation for Cooperative Multi-Agent Reinforcement Learning

Dec-POMDP

本文的研究对象是 decentralized partially observable Markov decision process (Dec-POMDP), 我们首先来看一下它和经典的MDP有什么不同?

(1) 奖励设定不同, 这里没有给到每一个agent的奖励, 只有一个整体奖励(team reward) $r_{tot}(\mathbf{s},\mathbf{u})$.
(2) 每个agent $i$ 观测到的不是它自己的状态 $s_i$, 它的观测要根据具体的设定来确定, 为表示区分常用 $o_i$ 来表示.
(3) 新增了一个叫做 view range 的概念, 每个 agent 都有一个 view range, 在这个范围里面的其他 agent 对它来说是有关联的, 也就是它们之间会相互影响, 且它的观测信息里包含它们的信息, 超出这个范围的 agent 视为无关, 完全独立, 其状态也不可见.

一些基本的符号: $N$: agent数量.

本文做了如下的一些假设:

reward 机制

考虑 agent $i$ 的奖励, 定义 agent $i$ 视野范围内的 agent 集合为它的团队(team), 记其数量为$M_i$, 作者认为 $i$ 自己的奖励 $r_{team}^i$ 与 joint state, joint action 有关, 而根据设定(3), 只有 view range 里的 agent 对它有影响, 因此只需包含 view range 里的 agent 的状态和动作, 根据设定, view range 里其他 agent 的状态信息在 $o_i$ 中包含, 在此基础上加上其它 agent 采取的动作 $u_i^{-}$, 以及agent $i$ 本身的动作 $u_i$, 即可得到 joint action, 所有 agent 获得的奖励之和是 team reward $r_{tot}$, 即

$$r_{tot}(\mathbf{s},\mathbf{u})=\sum _{i=1}^N{r}_{team}^i(o_i,u_i^{-},u_i)$$
对于 $r_{team}^i$ 的具体形式, 作者也做了如下的论断: 每一个 agent 都有一个 team, 同时它还可能在其他 agent的 team 里面, 作者认为 $Q_{tot}$ 的构成形式是, 每个 agent 的 team 都有一个 reward, 加和得到 $Q_{tot}$, 在一个 team 里面, team reward 又均匀分配给每个 agent. 每个 agent 最终得到的 reward 就是它从它所参与到的team 的 reward 里面分到的 reward 累加得到的. 打个比方, 有 10 个人, 每个人都有一个公司, 同时也在别人的公司里参股, 到年底分红时, (认为分红是均分), 每个人得到的钱是它创办/参股的公司的分红加和. 用符号语言描述如下:

$$r_{tot}(\mathbf{s},\mathbf{u})=\sum _{i=1}^N{\hat{r}}_1(o_i,u_i)+\sum _{1\le i<j\le N}{\hat{r}}_2(o_i,o_j,u_i,u_j)+...+{\hat{r}}_N(o_1,...,o_N,u_1,...,u_N)$$

其中 ${\hat{r}}_n(...)$ 表示由这 $n$ 个 agent 组成的所有 team 的 reward 之和, 如果这个team 不存在这一项就是 $0$, ${\hat{r}}_2(o_i,o_j,u_i,u_j)$ 是指 $i$, $j$ 组成的 team (例如 $i$ 为中心, 包含 $j$ 的team 和 $j$ 为中心, 包含 $i$ 的 team) 的 reward.

每一个 agent 的 reward 如下:

$$r_{team}^i(o_i,u_i^{-},u_i)={\hat{r}}_1(o_i,u_i)+\frac{1}{2}\sum _{1\le j\le N,j\ne i}{\hat{r}}_2(o_i,o_j,u_i,u_j)+...+\frac{1}{N}{\hat{r}}_N(o_1,...,o_N,u_1,...,u_N)$$

价值函数

team reward 对应得到的 Q 函数: $Q_{tot}^{\mathbf{\pi }}(\mathbf{s},\mathbf{u})$,
Q t o t π ( s , u ) = E τ ∼ π ∣ s 0 = s , u 0 = u { ∑ t = 0 ∞ γ t r t o t } = E τ ∼ π ∣ s 0 = s , u 0 = u { ∑ t = 0 ∞ γ t ∑ i = 1 N r t e a m i } = ∑ i = 1 N E τ ∼ π ∣ s 0 = s , u 0 = u { ∑ t = 0 ∞ γ t r t e a m i } Q_{tot}^{\bm\pi}(\bm{s}, \bm{u})=\mathbb{E}_{\bm\tau\sim \bm\pi|_{\bm{s_{0}}=\bm{s}, \bm{u_{0}}=\bm{u}}}\{\sum_{t=0}^{\infty}\gamma^{t}r_{tot}\}=\mathbb{E}_{_{\bm\tau\sim \bm\pi|_{\bm{s_{0}}=\bm{s}, \bm{u_{0}}=\bm{u}}}}\{\sum_{t=0}^{\infty}\gamma^{t}\sum_{i=1}^{N}r_{team}^{i}\} \\=\sum_{i=1}^{N}\mathbb{E}_{_{\bm\tau\sim \bm\pi|_{\bm{s_{0}}=\bm{s}, \bm{u_{0}}=\bm{u}}}}\{\sum_{t=0}^{\infty}\gamma^{t}r_{team}^{i}\} Qtotπ​(s,u)=Eτ∼π∣s0​=s,u0​=u​​{t=0∑∞​γtrtot​}=Eτ∼π∣s0​=s,u0​=u​​​{t=0∑∞​γti=1∑N​rteami​}=i=1∑N​Eτ∼π∣s0​=s,u0​=u​​​{t=0∑∞​γtrteami​}
定义 E τ ∼ π ∣ s 0 = s , u 0 = u { ∑ t = 0 ∞ γ t r t e a m i } = Q i π ( s i , u i − , u i ) \mathbb{E}_{_{\bm\tau\sim \bm\pi|_{\bm{s_{0}}=\bm{s}, \bm{u_{0}}=\bm{u}}}}\{\sum_{t=0}^{\infty}\gamma^{t}r_{team}^{i}\}=Q^{\bm{\pi}}_{i}(s_{i}, u_{i}^{-}, u_{i}) Eτ∼π∣s0​=s,u0​=u​​​{∑t=0∞​γtrteami​}=Qiπ​(si​,ui−​,ui​), 这里 $Q_i^{\mathbf{\pi }}(s_i,u_i^{-},u_i)$ 被称作agent $i$ 的 individual Q 函数,则 $Q_{tot}(\mathbf{s},\mathbf{u})$ 可以分解成这种形式:
$$Q_{tot}^{\mathbf{\pi }}(\mathbf{s},\mathbf{u})=\sum _{i=1}^N{Q}_i^{\mathbf{\pi }}(s_i,u_i^{-},u_i)$$
还可以得到如下的结论: ${\mathbf{u}}^{\ast }={\mathrm{argmax}}_{\mathbf{u}}{Q}_{tot}(\mathbf{s},\mathbf{u})$ 满足

$$u_i^{\ast }=\underset{u_i}{\mathrm{argmax}}{Q}_i^{\mathbf{\pi }}(s_i,u_i^{\ast -},u_i)$$

也就是说最佳的 joint action 一定是一个纳什均衡, 每一个 agent 站在自己的角度来看待自己的动作都是最优的.

策略

本文没有采用 actor network 来近似 policy, policy 的近似形式如下: 刚刚定义的 $Q_i^{\mathbf{\pi }}(s_i,u_i^{-},u_i)$ 被称作 centralized Q 函数, 下文中的下标中标注 $c$, 作者还为每个 agent 定义了一个函数 decentralized Q: $Q_i(s_i,u_i)$, 下文中的下标中标注 $p$, 且认为策略是对于这个 Q 函数 greedy 的:
$$\pi (s_i)=\underset{u_i}{\mathrm{argmax}}{Q}_{p,i}(s_i,u_i)$$

Q value function 的近似

把 $Q_i$ 近似地取成如下形式: $Q_{p,i}(s_i,u_i)\approx Q_{p,i}({\tau }_i,u_i)$, 其中 τ i , t = { o i , 1 , u i , 1 , . . . , o i , t } \tau_{i, t}=\{o_{i,1}, u_{i,1}, ..., o_{i,t}\} τi,t​={oi,1​,ui,1​,...,oi,t​}, 称为 history. $Q_{c,i}^{\mathbf{\pi }}(s_i,u_i^{-},u_i)$ 同理.

$Q_p$ 的 target

当 $M_i=0$ 时, $Q_{c,i}^{\mathbf{\pi }}(s_i,u_i^{-},u_i)$ 退化为只与 $s_i,u_i$ 有关, 因此文中把 $Q_{c,i}^{\mathbf{\pi }}(s_i,u_i^{-},u_i)$ 表示为

$$Q_{c,i}^{\mathbf{\pi }}(s_i,u_i^{-},u_i)=\{\begin{array}{llc}& Q_{coll,i}^{\mathbf{\pi }}(s_i,u_i^{-},u_i),& M_i>0\\ & Q_{alone,i}^{\mathbf{\pi }}(s_i,u_i),& M_i=0\end{array}$$
coll 是 collaborate 的缩写.

$\star$ $Q_p$ 的 target 如下:

$$L_p(\mu )=\{\begin{array}{llc}& \mathbb{E}[Q_{p,i}({\tau }_i,u_i)-{\varphi }_i^{\ast }({\tau }_i,u_i){]}^2,& M_i>0\\ & \mathbb{E}[Q_{p,i}({\tau }_i,u_i)-Q_{alone,i}^{\mathbf{\pi }}({\tau }_i,u_i)],& M_i=0\end{array}$$

其中 ${\varphi }_i^{\ast }({\tau }_i,u_i)=Q_{coll,i}^{\mathbf{\pi }}({\tau }_i,u_i^{\ast -},u_i)-Q_{coll,i}^{\mathbf{\pi }}({\tau }_i,u_i^{\ast -},u_i^{selfish})$
$(u_i^{\ast -},u_i^{\ast })={\mathrm{argmax}}_{u_i^{-},u_i}(Q_{coll}^i({\tau }_i,u_i^{-},u_i))$
${\varphi }_i^{\ast }({\tau }_i,u_i)$ 的意思是动作 $u_i$ 相较于完全 selfish 的动作的 advantage, 作者认为完全 selfish 的动作通常是最差的, 只有趋于合作才能提高 reward.
其他 agent 的动作为何选用 $u_i^{\ast -}$? 文中解释: we encourage the agent to learn each action’s value based on the optimistic belief that the possibility of other agents to take non-cooperative action is zero so that all other agents would cooperate with itself. As the main problem in the non-monotonic environment is that agents tend to take lazy actions fearing other agents not cooperating, this optimistic belief can facilitate exploration by increasing the probability of sampling cooperative actions and promises that agents will jump off the suboptimal policy to converge to the optimal cooperative policy. 简言之, 作者就是防止 agent 因为害怕其它 agent 不合作而采用不合作的动作, 所以在为 agent 选择动作的时候强行施加了一个 optimistic assumption, 让 agent 始终认为其他 agent 会和它合作.
selfish 的动作怎么选? 文中提出令 $u_i^{selfish}={\mathrm{argmax}}_{u_i}{Q}_{alone,i}^{\mathbf{\pi }}({\tau }_i,u_i)$. 当 $M_i=0$ 时, 说明它的 view range 里只有它自己, 此时的 $Q_{alone,i}^{\mathbf{\pi }}$ 可以认为是 selfish 的, 因此 selfish 的动作可以这么取.

采用 attention 机制对其他agent的信息进行 encode

为介绍原理, 我们引入论文 Actor-Attention-Critic for Multi-Agent Reinforcement Learning 中相关部分的介绍:
加入 agent $i$ 收到了一组其他 agent 的观测和动作信息: observation o = { o i } \bm{o}=\{o_{i}\} o={oi​}, $i=1,...,N$ 和 action a = { a i } \bm{a}=\{a_{i}\} a={ai​}, $i=1,...,N$, attention 机制是这样对其进行 encode 的：
(1) 对每个 agent 的 observation 和 action 进行编码, 采用一个 one-layer MLP 作为 embedding function, 记为 $e_k=g(o_k,a_k)$;
(2) 计算每个 agent $j\ne i$ 的信息重要程度, 以一个权重系数 ${\alpha }_j$ 表示, 称为 “attention 系数”:
$${\alpha }_j\propto \exp (e_j^T{W}_{key}^T{W}_{query}{e}_i)$$
这里 $W_{key}$ 和 $W_{query}$ 都是一个长宽等于 embedding 长度的方阵, 是可学习的变量组成的, 分别对 $e_j$ 和 $e_i$ 的信息进行二次提取, 提取后的信息称为 key 和 query. 其设计思想是这样的, $e_j^T{W}_{key}^T{W}_{query}{e}_i$ 实际上是对二次提取后的 embedding 信息进行一个内积, 计算其相近的程度, 这里 $\exp$ 函数防止梯度消失. 这里认为 embedding 和 $e_i$ 的 embedding 相似程度高的 agent 是重要的 agent, 因此又以其作为权重系数.
(3) 计算其他 agent 的信息 encode 的结果:
$$x_i=\sum _{j\ne i}{\alpha }_{j}h(Vg(o_i,a_i))$$
其中 $V$ 是一个 shared matrix, 也是可学习的参数组成的, $h$ 是 element-wise nonlinearity, 也就是激活函数, $h(Vg(o_i,a_i))$ 记作 $v_j$.

算法流程