反常积分
反常积分又叫广义积分,是对普通定积分的推广,指含有无穷上限/下限,或者被积函数含有瑕点的积分,前者称为无穷限广义积分,后者称为瑕积分(又称无界函数的反常积分)。
含有无穷上限/下限的反常积分
看到“无穷”这两个字,我们第一时间想到这玩意肯定跟极限有关系。但是转念一想,我们都是对函数求极限啊,怎么对积分求极限呢?
不要急。牛顿——莱布尼茨公式可是可以把积分转化为函数的。这样不就可以对把这类反常积分转化为函数的极限问题了吗。

含有瑕点的反常积分
瑕点就是瑕疵点,即不完美的点,意思就是这个点让积分看起来“不完美”了。不过在数学上,瑕点特指邻域内无界的点。
前面的含有无穷限的积分是因为“无穷”不是一个数,不能被代入牛顿——莱布尼茨公式。那么问题来了,为什么有瑕点的积分要被列为反常积分呢?

那么如何处理含有瑕点的积分呢?很简单,既然瑕点会影响积分的结果,那就想办法避开瑕点,但在避开瑕点的时候有不能影响积分的值。
那我们很自然的就可以想到可以靠无限逼近瑕点来实现在尽可能不影响结果的情况下避开瑕点。具体要从哪一侧逼近,要具体分析,去看从哪一侧逼近可以避开瑕点。
既然出现了“无限”一词,肯定又要用到极限了。具体的就不细说了,直接看例题。

我们学了两种反常积分,一种是含有无穷积分限的,另一种是含有瑕点的。解决这两种反常积分的方法都是利用极限。关键所在就是要把对积分的极限转化为对牛顿——莱布尼茨公式的极限。
广义积分是否收敛





欧拉-泊松积分
欧拉-泊松 积分,又叫概率积分,在概率论中有着重要的应用。




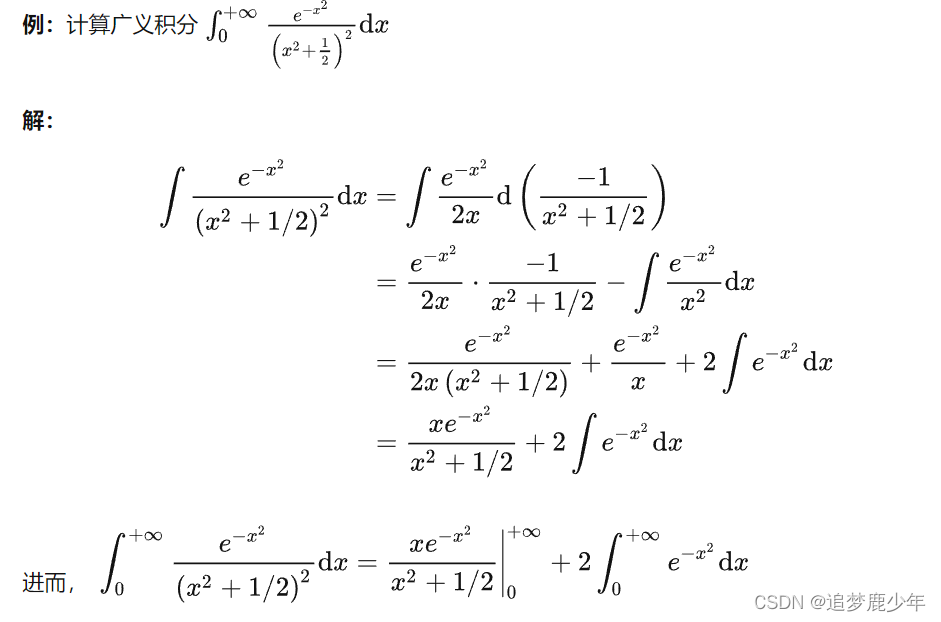
记一个方法:
τ
(
1
)
=
1
,
τ
(
1
2
)
=
π
,
τ
(
n
+
1
)
=
n
∗
τ
(
n
)
\tau (1)=1 , \tau(\frac{1}{2})=\sqrt{π} ,\tau(n+1)=n*\tau(n)
τ(1)=1,τ(21)=π,τ(n+1)=n∗τ(n)
∫ 0 ∞ t 1 2 . e − t d t = τ ( 1 2 + 1 ) \int_{0}^{∞} t^{\frac{1}{2}}.e-^t dt=\tau(\frac{1}{2}+1) ∫0∞t21.e−tdt=τ(21+1)= 1 2 \frac{1}{2} 21* τ ( 1 2 ) \tau(\frac{1}{2}) τ(21)= 1 2 \frac{1}{2} 21* π \sqrt{π} π