数据结构 - 快排 | C

news2025/6/18 18:33:20

目录

  • 快速排序
    • ①hoare版本
      • 思路分析
      • 代码实现
      • 时间复杂度
      • <整体优化>
      • <局部优化>
    • ②挖坑法
        • 思路分析
      • 代码实现
    • ③前后指针法
      • 思路分析
      • 代码实现
    • ④非递归快排
      • 思路分析
      • 代码实现
  • 以上代码汇总

快速排序

①hoare版本

思路分析

在这里插入图片描述
以上图为例：
指定一个数为a[key] = 6，a[right] 从尾出发找比 6 小的数，找到后停下，接着a[left] 从头出发找比 6 大的数，找到后停下 → Swap(&a[left], &a[right]) ，最终 a[right] 和 a[left] 相遇 → Swap(&a[key], &a[right]);//left==right

  • 这样就分割出了左右区间，左区间的数都比 6 小，右区间的数都比 6 大
  • 6 已经落到正确的位置
  • 解下来就是以左右区间为新数列，重复上述操作
    在这里插入图片描述
    Swap(&a[key], &a[right]);//left==right 分析：
  1. right 停住，left 往后走 与 right 相遇 ⇨ 相遇的位置是right 停住的位置 👉 right 找到要找的数才会停下（始终在 left < right 的约束下），此时相遇点就是 right 找到的比 a[key] 小的数
  2. left 停住，right 往前走 与 left 相遇 ⇨ 相遇的位置是 left 停住的位置 👉 right 比 left 先走，right 找到了 ，left 才会动，left停住之后，则会Swap(&a[left], &a[right]) ，Swap 之后此时a[left] < a[key] ，left 停住，right 往前走（如果一直未找到要找的数）与 left 相遇，此时相遇点就是比 a[key] 小的数

⭐左边做 key，右边先走；
⭐右边做 key，左边先走；
在这里插入图片描述

  • 一些bug代码分析：
while (left < right)
{
	while (a[right] > a[key])
	{
		--right;
	}
	while (a[left] < a[key])
	{
		++left;
	}
	Swap(&a[left], &a[right]);
}
Swap(&a[key], &a[right]);//left==right
  1. 相等的情况：
666
a[key]a[left]a[right]

Swap之后：

666
a[key]a[left]a[right]

这样循环就会卡住 👇

while (left < right)
{
	while (a[right] > a[key]){}//循环不进入
	while (a[left] < a[key]){}//循环不进入
	
	Swap(&a[left], &a[right]);//一直无限循环Swap
}
  1. 越界
while (left < right)
{
	while (a[right] >= a[key]){
		--right;
	}
	while (a[left] <= a[key]){
		++left;
	}
	Swap(&a[left], &a[right]);
}

right 飞出去的情况：

678961061314
a[key]

left 飞出去的情况：

616453623
a[key]

因此，right 和 left 每次改变之后都需要判断是否 left < right

代码实现

int hoareSort1(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;
	int key = left, begin = left, end = right;
	while (left < right)
	{
		while (left < right && a[right] >= a[key])
		{
			--right;
		}
		while (left < right && a[left] <= a[key])
		{
			++left;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[key], &a[right]);//left==right

	//[begin,left-1] [right+1,end]
	hoareSort1(a, begin, left - 1);
	hoareSort1(a, right + 1, end);

	return right;
}

时间复杂度

  • 最好的情况（像二叉树一样）：如下图 时间复杂度为O(N*logN)
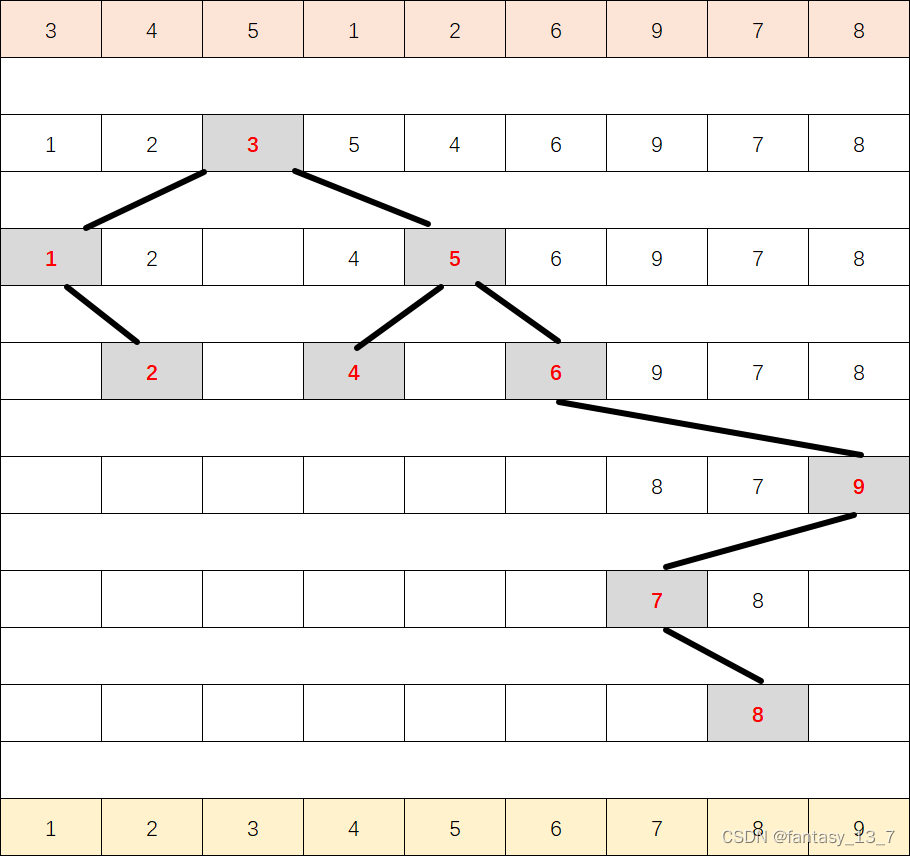
    在这里插入图片描述
  • 比较一般的情况：
    在这里插入图片描述
  • 最坏的情况：有序
    在这里插入图片描述
    Σ = n + (n-1) + (n-2) + …… + 2 + 1 = (n+1)*n/2
    ∴ 时间复杂度为 O(N²)

<整体优化>

  • 三数取中（begin、middle、end）
    • 例如：
123456789
[begin][middle][end]

∵ 1 < 6 < 9
∴ 选择 a[middle] 作为 a[key]

// 三数取中
int GetMidIndex(int* a, int left, int right)
{
	int begin = left, end = right;
	int middle = (left + right) / 2;

	if (a[begin] < a[end])
	{
		if (a[middle] < a[begin])
			return begin;
		else if (a[middle] > a[end])
			return end;
		else
			return middle;
	}
	else
	{
		if (a[middle] < a[end])
			return end;
		else if (a[middle] > a[begin])
			return begin;
		else
			return middle;
	}

}
// 快速排序hoare版本
int hoareSort1(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;
	int key = left, begin = left, end = right;

	int mid = GetMidIndex(a, left, right);

	Swap(&a[mid], &a[key]);
	while (left < right)
	{
		while (left < right && a[right] >= a[key])
		{
			--right;
		}
		while (left < right && a[left] <= a[key])
		{
			++left;
		}
		Swap(&a[left], &a[right]);
	}
	Swap(&a[key], &a[right]);//left==right

	//[begin,left-1] [right+1,end]
	hoareSort1(a, begin, left - 1);
	hoareSort1(a, right + 1, end);

	return right;
}

⭐int mid = GetMidIndex(a, left, right);
⭐Swap(&a[mid], &a[key]);

  • 为什么要Swap？ 如果不Swap↓
    在这里插入图片描述
    因为，最后 a[key] 会和 left 与 right 相遇的数交换，所以 [key] 必须在头部位置。

时间复杂度分析：针对局部有序或有序的情况效率明显提升
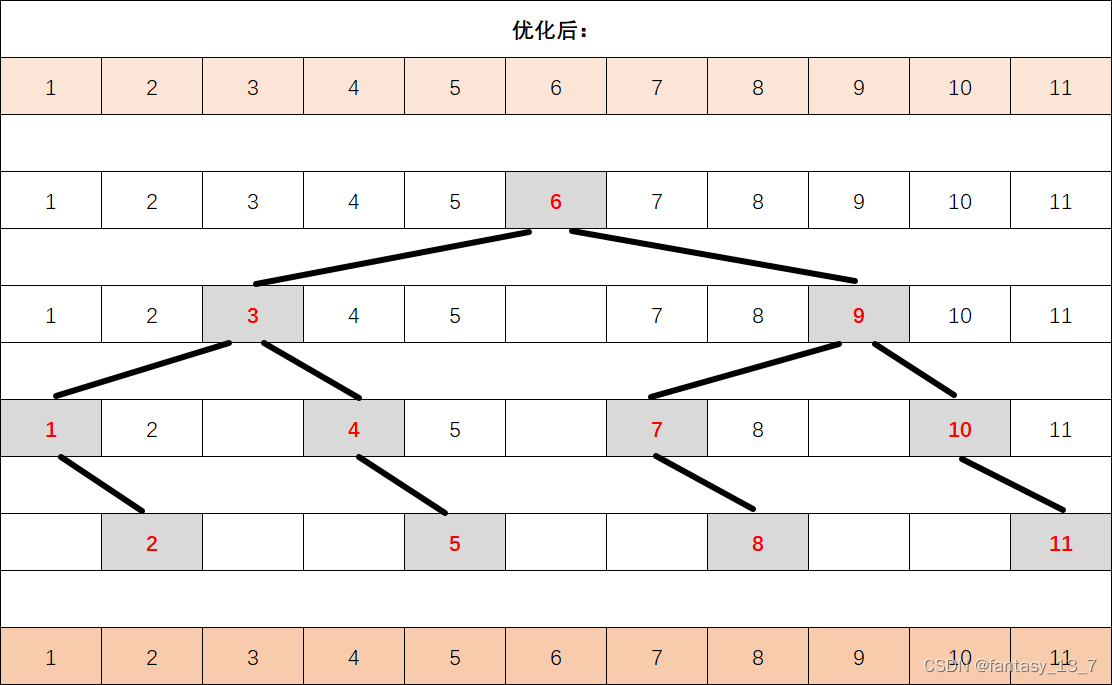
在这里插入图片描述
时间复杂度为 O(N) = N*logN

<局部优化>

递归到小区间的时候用插入排序
在这里插入图片描述

int hoareSort1(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;

	if ((right - left + 1) < 5)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		int key = left, begin = left, end = right;

		int mid = GetMidIndex(a, left, right);

		Swap(&a[mid], &a[key]);
		while (left < right)
		{
			while (left < right && a[right] >= a[key])
			{
				--right;
			}
			while (left < right && a[left] <= a[key])
			{
				++left;
			}
			Swap(&a[left], &a[right]);
		}
		Swap(&a[key], &a[right]);//left==right

		//[begin,left-1] [right+1,end]
		hoareSort1(a, begin, left - 1);
		hoareSort1(a, right + 1, end);
	}
	return right;
}

②挖坑法

思路分析

把选定做 key 的数存储在新变量中。left 和 right 找到 数 填坑里，原位置变新坑。
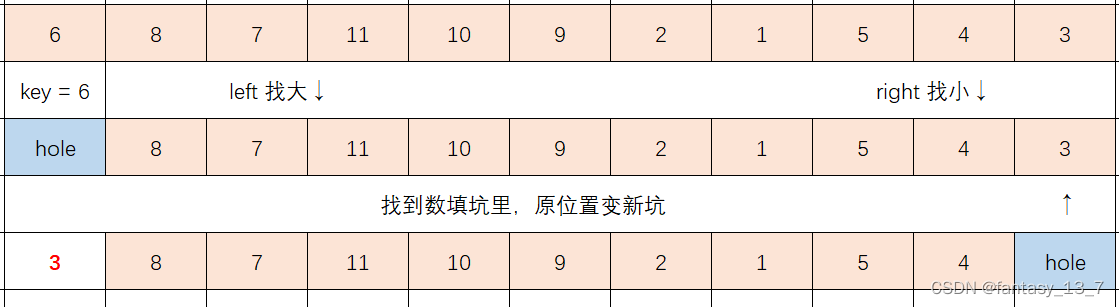
在这里插入图片描述

代码实现

// 快速排序挖坑法
int HoleSort2(int* a, int left, int right)
{
	if (left >= right)
		return;
	int key = a[left];
	int hole = left, begin = left, end = right;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			--right;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			++left;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[right] = key;

	//[begin,left-1] [right+1,end]
	HoleSort2(a, begin, left - 1);
	HoleSort2(a, right + 1, end);

	return right;
}

③前后指针法

思路分析

  1. cur 找比 key所指向 小的数
  2. 找到后，++prev，交换 cur 和 prev 指向的内容
  3. cur 走到尽头后，最后交换 key 和 prev
  • 小的数往前←，大的数往后→

cur 找到 比 data 小的数时的情况：👇
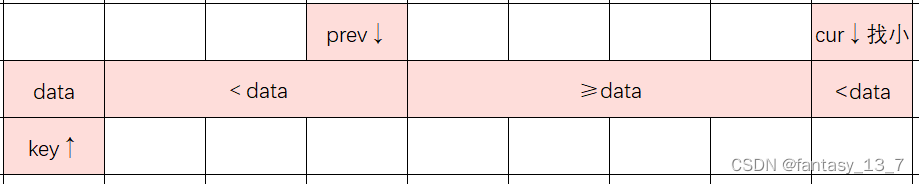
在这里插入图片描述
循环结束的情况：👇
在这里插入图片描述

  • 示例：
    在这里插入图片描述

代码实现

// 快速排序前后指针法
int PointSort3(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;
	int keyi = left;
	int prev = left, cur = left;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && cur != prev)
			Swap(&a[++prev], &a[cur]);

		++cur;
	}
	Swap(&a[keyi], &a[prev]);

	//[left,prev-1][prev+1,right]
	PointSort3(a, left, prev - 1);
	PointSort3(a, prev + 1, right);

	return prev;
}

④非递归快排

思路分析

利用数据结构栈 → 广度遍历
递归→ 深度遍历

  • 将左右区间[begin,end] 存入栈中
  • 循环：
    • 1.取出栈中的左右区间[begin,end]，在这个区间内进行快排
    • 2.一次快排之后，得到两个新的左右区间[begin,end] → [begin,keyi-1] keyi [keyi+1,end]，将其存入栈中（注意顺序）
    • 1.取出栈中的左右区间[keyi+1,end]，在在这个区间内进行快排
    • 2.一次快排之后，得到两个新的左右区间……
    • ……

代码实现

// 快速排序 非递归实现
#include "Stack.h"
void QuickSort(int* a, int left, int right)
{
	assert(a);
	Stack st;
	StackInit(&st);
	StackPush(&st, left);
	StackPush(&st, right);
	while (!StackEmpty(&st))
	{
		int end = StackTop(&st);
		StackPop(&st);
		int begin = StackTop(&st);
		StackPop(&st);
		int keyi = hoareSort1(a, begin, end);//快排

		//[begin,keyi-1] keyi [keyi+1,end]
		if (keyi + 1 < end)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, end);
		}
		if (begin < keyi - 1)
		{
			StackPush(&st, begin);
			StackPush(&st, keyi - 1);
		}
	}

	StackDestroy(&st);
}

以上代码汇总

// 快速排序递归实现
// 三数取中
int GetMidIndex(int* a, int left, int right)
{
	int begin = left, end = right;
	int middle = (left + right) / 2;

	if (a[begin] < a[end])
	{
		if (a[middle] < a[begin])
			return begin;
		else if (a[middle] > a[end])
			return end;
		else
			return middle;
	}
	else
	{
		if (a[middle] < a[end])
			return end;
		else if (a[middle] > a[begin])
			return begin;
		else
			return middle;
	}

}
// 快速排序hoare版本
int hoareSort1(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;

	if ((right - left + 1) < 5)
	{
		InsertSort(a + left, right - left + 1);
	}
	else
	{
		int key = left, begin = left, end = right;

		int mid = GetMidIndex(a, left, right);

		Swap(&a[mid], &a[key]);
		while (left < right)
		{
			while (left < right && a[right] >= a[key])
			{
				--right;
			}
			while (left < right && a[left] <= a[key])
			{
				++left;
			}
			Swap(&a[left], &a[right]);
		}
		Swap(&a[key], &a[right]);//left==right

		//[begin,left-1] [right+1,end]
		hoareSort1(a, begin, left - 1);
		hoareSort1(a, right + 1, end);
	}
	return right;

}


// 快速排序挖坑法
int HoleSort2(int* a, int left, int right)
{
	if (left >= right)
		return;
	int key = a[left];
	int hole = left, begin = left, end = right;
	while (left < right)
	{
		while (left < right && a[right] >= key)
		{
			--right;
		}
		a[hole] = a[right];
		hole = right;
		while (left < right && a[left] <= key)
		{
			++left;
		}
		a[hole] = a[left];
		hole = left;
	}
	a[right] = key;

	//[begin,left-1] [right+1,end]
	HoleSort2(a, begin, left - 1);
	HoleSort2(a, right + 1, end);

	return right;
}

// 快速排序前后指针法
int PointSort3(int* a, int left, int right)
{
	assert(a);
	if (left >= right)
		return;
	int keyi = left;
	int prev = left, cur = left;
	while (cur <= right)
	{
		if (a[cur] < a[keyi] && cur != prev)
			Swap(&a[++prev], &a[cur]);

		++cur;
	}
	Swap(&a[keyi], &a[prev]);

	//[left,prev-1][prev+1,right]
	PointSort3(a, left, prev - 1);
	PointSort3(a, prev + 1, right);

	return prev;
}

// 快速排序 非递归实现
void QuickSort(int* a, int left, int right)
{
	assert(a);
	Stack st;
	StackInit(&st);
	StackPush(&st, left);
	StackPush(&st, right);
	while (!StackEmpty(&st))
	{
		int end = StackTop(&st);
		StackPop(&st);
		int begin = StackTop(&st);
		StackPop(&st);
		int keyi = hoareSort1(a, begin, end);

		//[begin,keyi-1] keyi [keyi+1,end]
		if (keyi + 1 < end)
		{
			StackPush(&st, keyi + 1);
			StackPush(&st, end);
		}
		if (begin < keyi - 1)
		{
			StackPush(&st, begin);
			StackPush(&st, keyi - 1);
		}
	}

	StackDestroy(&st);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/411767.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

使用大华惠智双目半球网络摄像机DH-IPC-HD4140X-E2获取人流量统计数据

使用大华惠智双目半球网络摄像机DH-IPC-HD4140X-E2获取人流量统计数据

记录一下使用Java的SpringBoot大华SDK在智慧公厕项目中使大华惠智双目半球网络摄像机DH-IPC-HD4140X-E2获取人流量统计数据 首先根据说明书登录摄像头&#xff0c;一般摄像头都有自己的账号和密码(可能是admin admin 也可能是admin 888888 还有可能是admin 12345)&#xff0c;…
阅读更多...
VMware ESXi 7.0 U3l Unlocker OEM BIOS 集成网卡驱动和 NVMe 驱动 (集成驱动版)

VMware ESXi 7.0 U3l Unlocker OEM BIOS 集成网卡驱动和 NVMe 驱动 (集成驱动版)

ESXi 7 U3 标准版集成 Intel 网卡、USB 网卡 和 NVMe 驱动 请访问原文链接&#xff1a;https://sysin.org/blog/vmware-esxi-7-u3-sysin/&#xff0c;查看最新版。原创作品&#xff0c;转载请保留出处。 作者主页&#xff1a;sysin.org 2023-03-31&#xff0c;发布 ESXi 7.0U…
阅读更多...
C++轻量级Web服务器TinyWebServer源码分析之log篇

C++轻量级Web服务器TinyWebServer源码分析之log篇

文章目录log日志篇简介一、日志类的定义与使用二、单例模式与阻塞队列的定义1、单例模式2、阻塞队列log日志篇简介 使用单例模式创建日志系统&#xff0c;对服务器运行状态、错误信息和访问数据进行记录&#xff0c;该系统可以实现按天分类&#xff0c;超行分类功能。其中异步…
阅读更多...
RabbitMq图形界面创建队列操作步骤及控制台使用说明

RabbitMq图形界面创建队列操作步骤及控制台使用说明

版本&#xff1a;RabbitMQ 3.9.7 控台台访问路径&#xff1a; http://localhost:15672/#/queues 使用控制台创建队列 登录 创建队列 &#xff08;1&#xff09;输入自定义的队列名称 &#xff08;2&#xff09;其他输入参数为默认值即可 &#xff08;3&#xff09;点击【Add…
阅读更多...
雷蛇灵刃18 2023原厂预装出厂Windows11系统

雷蛇灵刃18 2023原厂预装出厂Windows11系统

雷蛇系统安装完自带所有机型驱动和软件&#xff0c;并重建隐藏分区&#xff0c;还原功能 文件地址: https://pan.baidu.com/s/1snKOsH3OMl3GZLqeAf-GLA?pwd8888 支持系列: 雷蛇灵刃16 2023 [RZ09-0483]Windows11原厂系统 雷蛇灵刃 Stealth 13 Base Model [RZ09-0310] 201…
阅读更多...
【Unity VR开发】结合VRTK4.0：创建一个按钮（Option Button）

【Unity VR开发】结合VRTK4.0：创建一个按钮（Option Button）

语录&#xff1a; 如同天上降魔主&#xff0c;真是人间太岁神。 前言&#xff1a; 选项按钮是一种提供多项选择选项的方法&#xff0c;其中只有一个按钮可以处于激活状态&#xff0c;激活另一个按钮时将确保组中的所有其他按钮都已停用。我们可以使用嵌套在预制件中的预制件来实…
阅读更多...
ChatGPT将引发大量而普遍的网络安全隐患

ChatGPT将引发大量而普遍的网络安全隐患

ChatGPT是一个基于人工智能的语言生成模型&#xff0c;它可以在任何给定的时间&#xff0c;使用自然语言生成技术&#xff0c;生成文本、对话和文章。它不仅可以被用来编写文本&#xff0c;还可以用来编写语言、生成图像和视频。目前&#xff0c; ChatGPT已广泛应用于语言翻译、…
阅读更多...
FPGA lattice 深力科LCMXO3LF-4300C-6BG256I 可实现高效、灵活和安全的工业应用开发 低功耗FPGA解决方案详情讲解

FPGA lattice 深力科LCMXO3LF-4300C-6BG256I 可实现高效、灵活和安全的工业应用开发 低功耗FPGA解决方案详情讲解

FPGA lattice 深力科LCMXO3LF-4300C-6BG256I 可实现高效、灵活和安全的工业应用开发 低功耗FPGA解决方案详情讲解 超低密度FPGA 是最新的立即启用、非挥发性、小型覆盖区 FPGA&#xff0c;采用先进的封装技术&#xff0c;能让每个元件达到最低成本。此系列采用最新的小型封装&…
阅读更多...
RK3399平台开发系列讲解（基础篇）Linux 传统间隔定时器

RK3399平台开发系列讲解（基础篇）Linux 传统间隔定时器

🚀返回专栏总目录 文章目录 一、设置间隔定时器 setitimer()二、查询定时器状态 getitimer()三、更简单的定时接口 alarm()四、传统定时器的应用4.1、为阻塞操作设置超时4.2、性能剖析五、传统定时器的局限性沉淀、分享、成长，让自己和他人都能有所收获！😄 📢本篇将详细…
阅读更多...
java 泛型 万字详解（通俗易懂)

java 泛型 万字详解（通俗易懂)

目录 一、前言 二、为什么需要泛型&#xff1f; 三、什么是泛型&#xff1f; 1.泛型的定义 : 2.泛型的作用 : 四、怎么用泛型&#xff1f; 1.泛型的语法 : 2. 泛型的使用 : 3.自定义泛型类 : 1 基本语法 : 2 使用细节 : 4.自定义泛型接口 : 1 基本语法 : 2 使用细…
阅读更多...
C++-继承

C++-继承

继承继承的基本概念继承的概念继承的定义继承的格式继承的方式继承基类成员访问方式的变化基类与派生类的对象赋值转换继承中的作用域派生类中的默认成员函数继承与友元继承中的静态成员菱形继承菱形虚拟继承继承的总结继承的基本概念 继承的概念 继承机制是面向对象程序设计中…
阅读更多...
【Spring源码】 BeanFactory和FactoryBean是什么？

【Spring源码】 BeanFactory和FactoryBean是什么？

1、前言 面试官&#xff1a;“看过Spring源码吧&#xff0c;简单说说Spring中BeanFactory和FactoryBean的区别是什么&#xff1f;” 大神仙&#xff1a;“BeanFactory是bean工厂&#xff0c;FactoryBean是工厂bean”。 这么回答&#xff0c;等于面试官问你Spring是什么&…
阅读更多...
如何免费使用ChatGPT 4？

如何免费使用ChatGPT 4？

自从ChatGPT发布以来&#xff0c;它就取得了巨大的成功。无论是常春藤法学考试还是商学院作业&#xff0c;ChatGPT都被用于各种试验。统计数据显示&#xff0c;ChatGPT每月吸引约9600万用户。随着ChatGPT的巨大成功&#xff0c;Open AI最近推出了它的最新版本&#xff0c;名为“…
阅读更多...
Learning to Detect Human-Object Interactions 文章解读

Learning to Detect Human-Object Interactions 文章解读

Learning to Detect Human-Object Interactions&#xff0c;WACV&#xff0c;2018 论文下载 code&#xff1a;http://www.umich.edu/∼ywchao/hico/ 摘要 主要研究领域&#xff1a;定义了HOI detection任务&#xff1a;在静态图像中检测人-对象交互&#xff08;HOI&#xff…
阅读更多...
Vue路由模式为history的项目部署到Nginx

Vue路由模式为history的项目部署到Nginx

前言 对于前端工程师而言&#xff0c;多多少少会碰到按需加载的需求。 比如一个系统&#xff0c;需要用户登陆以后才能使用&#xff0c;对于传统的前后端未分离的情况&#xff0c;我们一般的处理方式是&#xff0c;当检测到用户未登录的时候&#xff0c;一般会重定向到登录页面…
阅读更多...
JVM运行时数据区的必备知识：Java程序员不容错过

JVM运行时数据区的必备知识：Java程序员不容错过

1、JVM运行时数据区概念 JVM运行时数据区是Java虚拟机在执行Java程序时所使用的内存区域。这些区域包括了以下几个部分&#xff1a; 程序计数器&#xff08;Program Counter Register&#xff09;&#xff1a;程序计数器是一块较小的内存区域&#xff0c;它可以看作是当前线程…
阅读更多...
测试1号位的自我修养

测试1号位的自我修养

作者&#xff1a;京东零售 吴聪 引言 目前京东实行BigBoss机制以及积木型组织&#xff0c;同时现阶段再次强调了“经营”理念&#xff0c;以上均是比较大的组织层面的纲领和引导&#xff0c;核心是为了激发大家owner意识可以更好更快为公司产出价值和贡献。落到具体执行层面&…
阅读更多...
国内大模型领域进入乱战时代

国内大模型领域进入乱战时代

国内大模型领域进入乱战时代 2023.4.12版权声明&#xff1a;本文为博主chszs的原创文章&#xff0c;未经博主允许不得转载。 什么是大模型 大模型&#xff0c;又称为预训练模型、基础模型等&#xff0c;是指模型参数数量很大&#xff0c;需要大量计算资源才能训练的深度学习…
阅读更多...
RHCE-Web服务器

RHCE-Web服务器

请给openlab搭建web网站​ 网站需求&#xff1a;​ 1.基于域名[www.openlab.com](http://www.openlab.com)可以访问网站内容为 welcome to openlab!!! 首先创建一个名为openlab的网站&#xff1a; &#xff08;1&#xff09;在www目录下创建一个openlab文件夹&#xff1a;mk…
阅读更多...
Android UI

Android UI

什么是 UI 用户界面&#xff08;User Interface&#xff0c;简称 UI&#xff0c;亦称使用者界面&#xff09;是系统和用户之间进行交互和信息交换的媒介&#xff0c;它实现信息的内部形式与人类可以接受形式之间的转换。软件设计可分为两个部分&#xff1a;编码设计与UI设计。A…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023