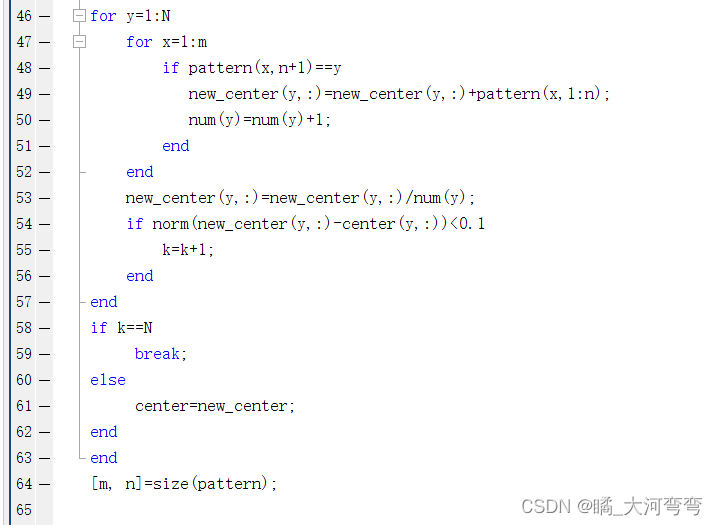
思维导图:
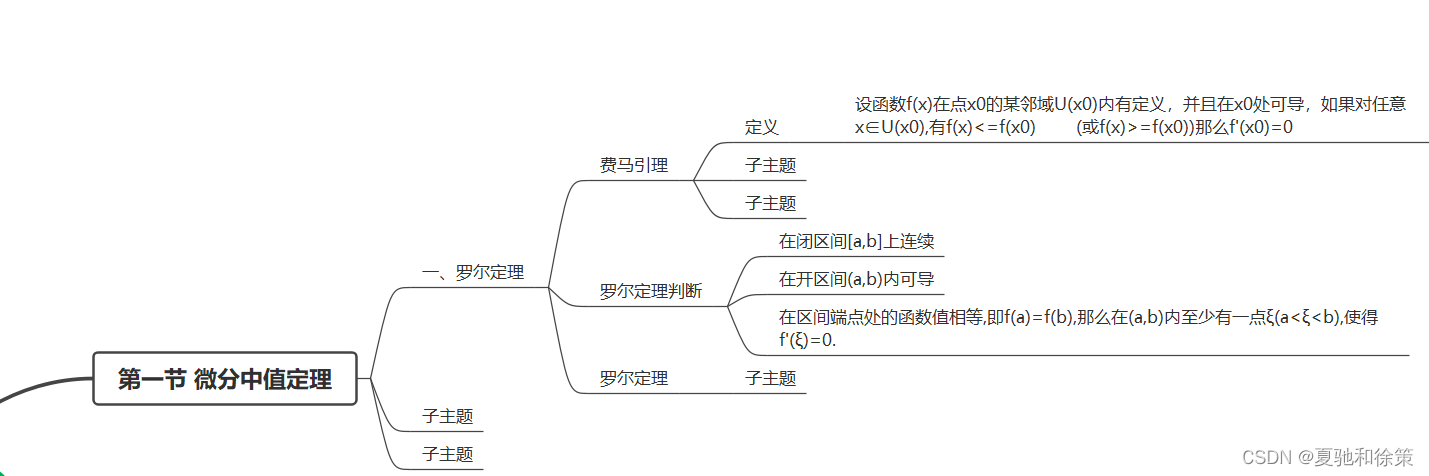
学习目标:
我会按照以下步骤来学习微分中值定理:
- 理解导数的定义和性质:在学习微分中值定理之前,首先要对导数的定义和性质有一个清晰的理解,包括导数的几何意义和导数存在的条件等。
- 学习拉格朗日中值定理:罗尔定理是拉格朗日中值定理的特殊情况,因此在学习罗尔定理之前,我会先学习拉格朗日中值定理,理解其原理和应用场景。
- 掌握证明方法:掌握拉格朗日中值定理的证明方法,这可以帮助我更深入地理解这个定理。
- 学习柯西中值定理:柯西中值定理是拉格朗日中值定理的推广,可以解决更一般的情况,因此我会学习柯西中值定理及其证明方法。
- 理解应用场景:学习微分中值定理不仅要理解其数学原理,还要了解其在实际问题中的应用场景,如求极值、证明不等式等。
- 刷题巩固:最后,我会通过刷题来巩固所学知识,不断加深对微分中值定理的理解和应用能力。




我的理解:
- 罗尔定理是微积分中的一条重要定理,它描述了在一定条件下,函数在某个区间内的导数等于零,则函数在该区间内存在至少一个驻点(即导数为零的点)。
- 换句话说,罗尔定理告诉我们,如果一个函数在区间两端的函数值相等,并且在该区间内的导数存在,那么在该区间内至少存在一个导数为零的点。
- 这个定理的意义在于,如果我们需要确定一个函数在某个区间内的极值点,那么可以首先找到导数为零的点,然后在这些点中寻找极值点。因此,罗尔定理在微积分中具有重要的应用价值。
- 需要注意的是,罗尔定理仅适用于闭区间上的函数,并且导数存在。如果函数不满足这些条件,那么罗尔定理可能不成立。



 我的理解:
我的理解:
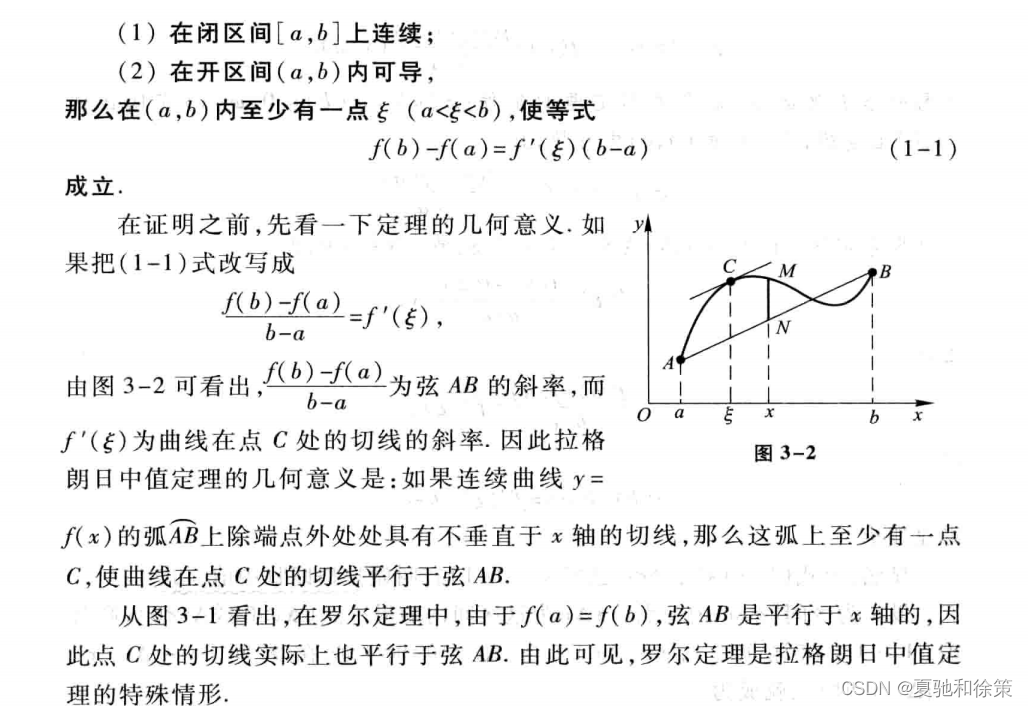
- 拉格朗日中值定理是微积分中的一个重要定理,它描述了在一定条件下,函数在某个区间内的导数等于函数在该区间内两个端点的函数值之差与两个端点的横坐标之差的商,则函数在该区间内至少存在一个点的导数等于该商。
- 换句话说,拉格朗日中值定理告诉我们,如果一个函数在闭区间上连续,在该区间内可导,那么在该区间内至少存在一个点,使得该点的导数等于该函数在两个端点的函数值之差与两个端点的横坐标之差的商。
- 这个定理的意义在于,它为我们提供了一种求函数在某个区间内的平均变化率的方法。具体来说,该区间内的平均变化率等于函数在两个端点的函数值之差与两个端点的横坐标之差的商,而根据拉格朗日中值定理,该平均变化率等于函数在某个点的导数。
- 需要注意的是,拉格朗日中值定理仅适用于闭区间上的函数,并且假设函数在该区间内连续,在该区间内可导。如果函数不满足这些条件,那么拉格朗日中值定理可能不成立。






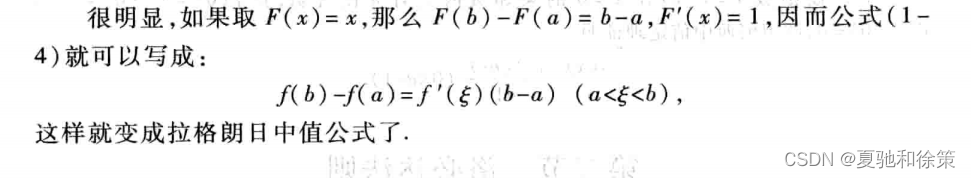 我的理解:
我的理解:
- 柯西中值定理是微积分中的一个重要定理,它描述了在一定条件下,两个函数在某个区间内的导数之比等于两个函数在该区间内某个点的函数值之比与该点的横坐标与两个端点横坐标之差的商相等。
- 换句话说,柯西中值定理告诉我们,如果两个函数在闭区间上连续,在该区间内可导,且其中一个函数在该区间内的导数不为零,那么在该区间内至少存在一个点,使得这两个函数在该点的函数值之比等于两个函数在两个端点的函数值之比与两个端点的横坐标之差的商相等。
- 这个定理的意义在于,它为我们提供了一种求两个函数在某个区间内某个点的斜率相等的方法。具体来说,如果两个函数在某个点的斜率相等,那么根据柯西中值定理,这两个函数在该点的函数值之比等于两个函数在两个端点的函数值之比与两个端点的横坐标之差的商相等。
- 需要注意的是,柯西中值定理仅适用于闭区间上的函数,并且假设函数在该区间内连续,在该区间内可导,且其中一个函数在该区间内的导数不为零。如果函数不满足这些条件,那么柯西中值定理可能不成立。
总结:
- 罗尔定理、拉格朗日中值定理和柯西中值定理在微积分中有广泛的应用,下面是它们一些常见的应用:
- 确定函数的最值:通过拉格朗日中值定理或柯西中值定理,我们可以确定函数在某个区间内的最大值或最小值。
- 求函数的导数:通过柯西中值定理,我们可以求出函数在某个区间内的导数。
- 确定曲线的切线和法线:通过拉格朗日中值定理,我们可以确定曲线在某个点处的切线和法线的斜率和方程式。
- 确定函数的凸性和凹性:通过柯西中值定理,我们可以确定函数在某个区间内的凸性和凹性。
- 求积分:柯西中值定理可以用于证明牛顿-莱布尼茨公式,即求解定积分时可以通过求导得到原函数。
- 总的来说,这些中值定理为微积分的应用提供了有力的工具,使我们能够更好地理解和处理各种微积分问题。