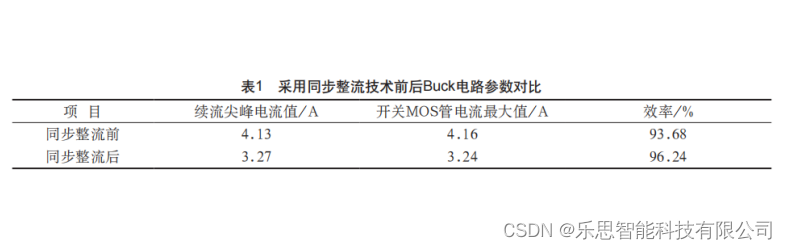
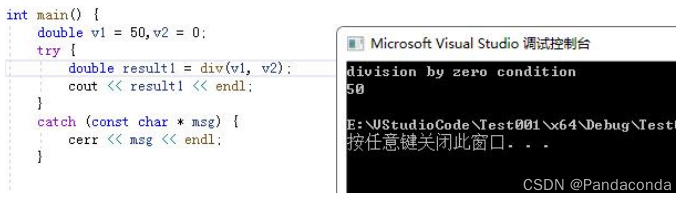
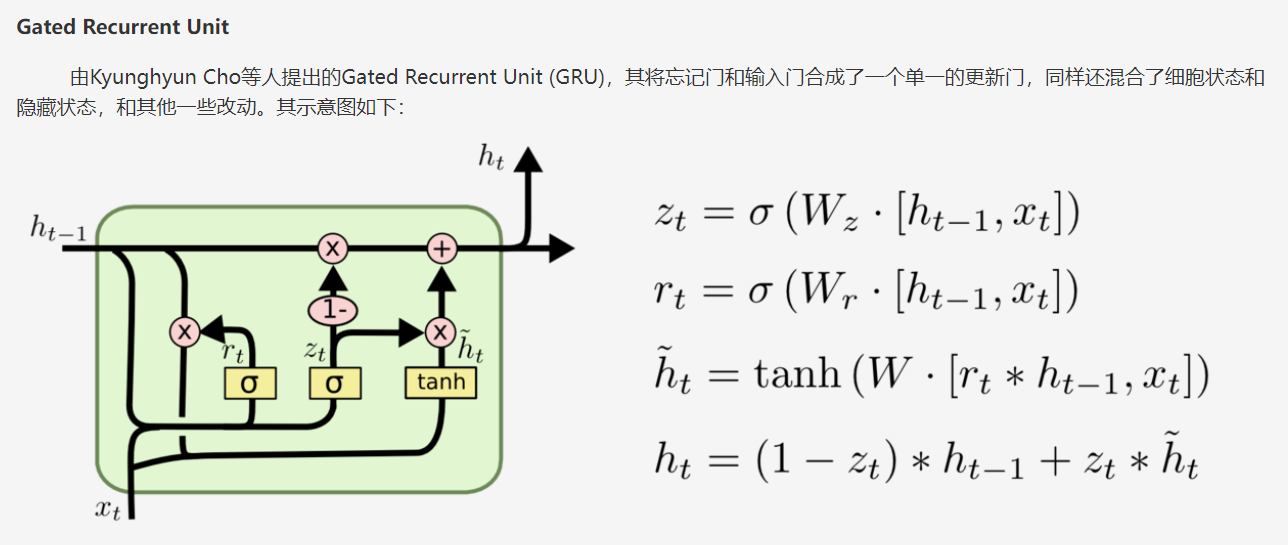
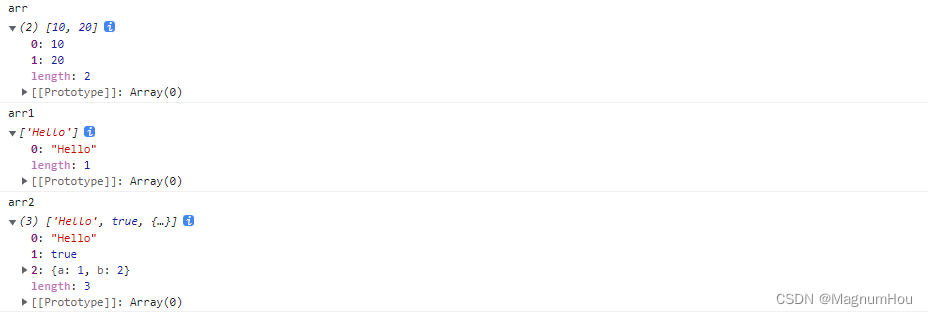
T1 - 直径

思路

就类似下图的链接方法。

这其中每一条边权都是 $1$。

我们设以 $2$ 为根的子树除去 $2$ 有 $a$ 个节点，以 $3$ 为根的子树除去 $3$ 有 $b$ 个节点，以 $4$ 为根的子树除去 $4$ 有 $c$ 个节点。

此时直径的数量就为 $a\cdot b+a\cdot c+b\cdot c$。

我们可以枚举 $a,b$ ，看下有没有相应的 $c$ 满足条件就可以了。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL k;
void out3(int a, int b, int c) {
    printf("%d\n", 4 + a + b + c);
    printf("1 2 1\n1 3 1\n1 4 1\n");
    for (int i = 5; i <= a + 4; i++)
        printf("2 %d 1\n", i);
    for (int i = a + 5; i <= a + 4 + b; i++)
        printf("3 %d 1\n", i);
    for (int i = a + b + 5; i <= a + 4 + b + c; i++)
        printf("4 %d 1\n", i);
}
int main() {
    // freopen("diameter.in", "r", stdin);
    // freopen("diameter.out", "w", stdout);
    scanf("%lld", &k);
    for (LL i = 1; i <= 5000; i++)
        for (LL j = 1; j <= 5000 - i; j++)
            if ((k - i * j) % (i + j) == 0 && (k - i * j) / (i + j) + j + i + 4 <= 5000) {
                out3(i, j, (k - i * j) / (i + j));
                return 0;
            }
    return 0;
}

T2 - 定价

思路

因为查询比较少，所以我们可以每次查询都做一次。

我们来看看如何做查询。

我们先将限制看为 $0$ 和 $1$，$0$ 代表只能选 $0$，$1$ 代表 $0$ 和 $1$ 都能选。

我们可以从高位往低位枚举，因为我们已经知道上一个套装的选择方案了，于是我们分以下 $4$ 类情况。

• 如果上一位选了 $1$，这一位为 $1$，则这一位的一必须选。
• 如果上一位选了 $0$，这一位为 $1$，则我们可以将这一位选上，更新当前套装的答案，但在再往低位枚举时就不用将这一位选上。
• 如果上一位选了 $1$，这一位为 $0$，则我们直接退出当前套装的枚举。
• 如果上一位选了 $0$，这一位为 $0$，则我们不用管他。

此时我们看看当前套装的答案有没有被更新过，如果没有，就说明没有一种方案满足要求，直接输出 $-1$ 就好了。

因为这样做是 $O(nm)$，我们来想想怎么优化。

因为只有为 $1$ 的位才有贡献，所以我们可以用 set 来存每一位的限制，然后枚举时用双指针来做就可以了。

具体实现可以看代码。

注意 set 的细节，很容易越界导致gg。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD = 1e9 + 7;
int n, m, q;
LL ans, sum;
set <int> st[1005], last, now, s;
LL Pow(LL a, int b) {
    LL s = 1;
    while (b) {
        if (b & 1)
            s = s * a % MOD;
        a = a * a % MOD, b = b >> 1;
    }
    return s;
}
int main() {
    set <int>::const_iterator it, jt, lt;
    scanf("%d%d%d", &n, &m, &q);
    for (int qq = 1, op, r, c; qq <= q; qq++) {
        scanf("%d", &op);
        if (op == 1) {
            scanf("%d%d", &r, &c);
            if (st[r].count(m - c))
                st[r].erase(m - c);
            else
                st[r].insert(m - c);
        }
        else {
            last.clear();
            if (st[1].empty()) {
                printf("-1\n");
                continue;
            }
            last.insert(*st[1].begin());
            ans = Pow(2, *st[1].begin());
            //第一位特殊判断，直接使得第一位最小就可以了。
            for (int i = 2; i <= n; i++) {
                if (st[i].empty()) {//如果这一位没有任何1，直接为-1就可以了
                    ans = -1;
                    break;
                }
                jt = last.end(), jt--, it = st[i].upper_bound(*jt), sum = 0, s.clear(), now.clear();
                if (it == st[i].end())
                    it--;
                for (; ;) {
                    if (*jt == *it) {//上一个选了1，这一位为1
                        now.insert(*it);
                        if (it == st[i].begin())
                            break;
                        if (jt == last.begin()) {
                            s = now;
                            s.insert(*st[i].begin());
                            break;
                        }
                        jt--, it--;
                    }
                    else if (*jt > *it)//上一个选了1，这一位为0
                        break;
                    else {//上一个选了0，这一位为1
                        s = now;
                        s.insert(*it);
                        if (it == st[i].begin())
                            break;
                        it--;
                    }
                }
                if (s.empty())//如果答案没有被更新过
                    ans = -1;
                if (ans == -1)
                		break;
                last.clear();
                for (it = s.begin(); it != s.end(); it++)
                    sum = (sum + Pow(2, *it)) % MOD, last.insert(*it);
                (ans += sum) %= MOD;
            }
            printf("%lld\n", ans);
        }
    }
    return 0;
}

T3 - 排序

思路

我们可以将 $cnt$ 次操作后能做完几个整轮，我们假设能做完 $k$ 个整轮，则我们可以先将 $k$ 个整轮之后的数组求出来，剩下的再暴力做。

我们来看看怎么求出 $k$ 轮之后的数组。

我们先用一个优先队列存 $k$ 个数，表示比当前的数小的前 $k$ 个位置。

那我们做完 $k$ 轮之后，当前数就会到这 $k+1$ 个位置中的最后一个位置。

原理比较难讲，自己理解一下应该可以。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, a[1000005], ans[1000005], tr[100000005], b[1000005];
LL cnt, m;
LL in() {
    LL s = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9')
        ch = getchar();
    while (ch <= '9' && ch >= '0')
        s = s * 10 + ch - '0', ch = getchar();
    return s;
}
int main() {
    // freopen("sort.in", "r", stdin);
    // freopen("sort.out", "w", stdout);
    n = in(), m = cnt = in();
    for (int i = 1; i <= n; i++)
        a[i] = in(), b[a[i]] = i;
    priority_queue <int> q;
    int k = 1;
    while (m >= n - k)
        m = m - n + k, k++;
    k--;
    if (k) {
        for (int i = 1; i <= k; i++)
            q.push(b[i]);
        for (int i = k + 1; i <= n; i++) {
            if (q.top() > b[i])
                ans[q.top()] = i, q.pop(), q.push(b[i]);
            else
                ans[b[i]] = i;
        }
        for (int i = 1; i <= k; i++)
            ans[i] = i;
    }
    else
        for (int i = 1; i <= n; i++)
            ans[i] = a[i];
    // for (int i = 1; i <= n; i++)
    //     printf("%d ", ans[i]);
    // printf("\n");
    k++;
    for (int j = k + 1; m > 0 && j <= n; j++) {
        if (ans[j] < ans[k])
            swap(ans[j], ans[k]);
        m--;
    }
    for (int i = 1; i <= n; i++)
        printf("%d ", ans[i]);
    return 0;
}