在本文中，我们通过一个名为WinBUGS的免费贝叶斯软件，可以很容易地完成基于似然的多变量随机波动率（SV）模型的估计和比较。

最近我们被客户要求撰写关于随机波动率的研究报告，包括一些图形和统计输出。通过拟合每周汇率的双变量时间序列数据，多变量SV模型，包括波动率中的格兰杰因果关系，时变相关性，重尾误差分布，加性因子结构和乘法因子结构来说明想法。

单变量随机波动率（SV）模型为ARCH类型模型提供了有效的替代方案，可以解释波动率的条件和无条件属性。

多元SV模型

金融资产收益的程式化事实

考虑到多变量SV模型对于描述金融资产收益的动态最有用，我们首先总结一些记录良好的金融资产收益的程式化事实：

1. 资产收益分配是尖峰厚尾特征。

2. 资产收益率波动率集群。

3. 收益率是交叉相关的。

4. 波动性是交叉依赖的。

5. 一种资产格兰杰的波动导致另一种资产的波动。

6. 通常存在较低维度因子结构，可以解释大部分相关性。

7. 相关性是随时间变化的。

除了这七个事实之外，诸如参数空间的维数和协方差矩阵的正半确定性之类的问题具有实际重要性。当我们审查现有模型并介绍我们的新模型时，我们将评论它们处理程式化事实和上述两个问题的适当性。

为了说明替代多变量SV模型之间的差异和联系，我们关注本文中的双变量情况。特别是，我们考虑了九种不同的双变量SV模型（带粗体的首字母缩略词）。此外，这些模型中的大多数都适用于多维变量，而模型5是唯一的例外。

模型1（基本MSV或MSV）。 该模型相当于将两个基本单变量SV模型组合在一起。显然，该模型不允许交叉收益或波动率之间的相关性，也不允许Granger因果关系。但是，它允许尖峰厚尾特征收益率分布和波动率聚类。

模型2（常数相关MSV或CC-MSV） 在该模型中，允许收益率冲击相关，因此该模型类似于Bollerslev的常数条件相关（CCC）ARCH模型。因此，收益率是相互依赖的。

模型3（具有格兰杰因果关系或GC-MSV的MSV）。 由于φ 21可以是不同于零，第二资产的波动允许是格兰杰由第一资产的波动。因此，收益率和波动率都是相互依赖的。然而，波动率的交叉依赖性是通过格兰杰因果关系和波动率聚类共同实现的。此外，当两个φ 12和φ 21是非零，在两种资产之间波动双向Granger因果关系是允许的。据我们所知，该模型是SV文献的新增内容。

使用WinBUGS进行贝叶斯估计

模型通过对所有未知参数a  =（a 1，...，a p）的先验分布的设置来完成。例如，在模型1（MSV）中，p  = 6和未知参数的矢量a 。贝叶斯推断基于模型中所有未观察量θ的联合后验分布。矢量θ包括未知参数和潜在对数波动率的矢量，即θ  =（a，h 1，...，h T）。 

实证说明

数据

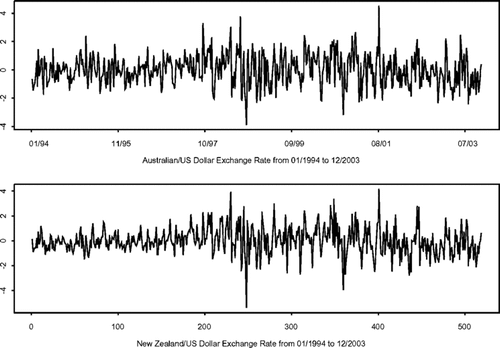
在本节中，我们将介绍的模型拟合实际经济时间序列数据。从1994年1月到2003年12月，所使用的数据是每周澳大利亚和新西兰汇率的平均调整对数收益率。这两个序列的选择是因为这两个经济体彼此紧密相连，因此事先预计两种汇率之间的依赖性很强。这两个系列在图中绘制，其中收益率和波动率的交叉依赖性确实显得很强。

汇率收益率的时间序列图。

Basis MSV

基础msv

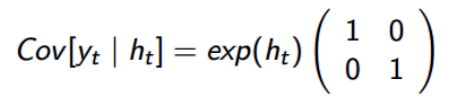
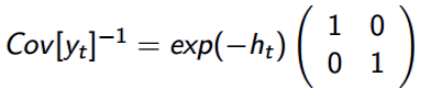
由于非标准化的参数设置，模拟

代码片段：

model volatility;
{for (i in 1:N) {
Yisigma2a[i] <- exp(-th[i,1]);
Yisigma2b[i] <- exp(-th[i,2]);
Y[i,1]~ dnorm(0,Yisigma2a[i]);
Y[i,2]~ dnorm(0,Yisigma2b[i]

th[1,1]~dnorm(thmean[1,1],itaua2);
th[1,2]~dnorm(thmean[1,2],itaub2
for (i in 2:N) {
thmean[i,1] <- mu1 + phi1*(th[i-1,1]-mu1);
thmean[i,2] <- mu2 + phi2*(th[i-1,2]-mu2

MSV  Granger Causality GC-MSV

代码片段：

model volatility;
{ for (i in 1:N) {
ysigmadet[i]<-exp(th[i,1]+th[i,2])*(1-rhoep*rhoep;
Yisigma2[i,1,1] <- exp(th[i,2])/ysigmadet[i;



Yisigma2[i,2,1] <- Yisigma2[i,1,2;



for (i in 2:N) {
thmean[i,1] <- mu1 + phi1*(th[i-1,1]-mu1)+phi12*(th[i-1,2]-mu2);
thmean[i,2] <- mu2 + phi2*(th[i-1,2]-mu2)

结果

我们报告前六个模型的后验分布的平均值，标准误差和95％可信区间以及最后三个模型的后验分布，以及为九个中的每一个生成100次迭代的计算时间。

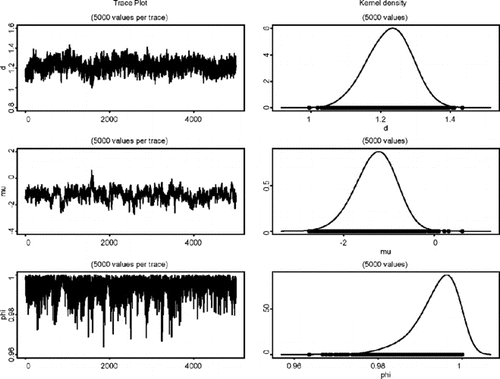
模型（AFactor-t-MSV）中d，μ和φ 的边缘分布的曲线图和密度估计值。

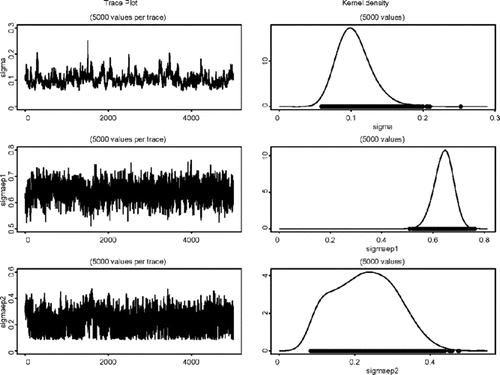
σ的边缘分布的密度估计η，σ ε1 ，和σ ε2在模型（AFactor MSV）。

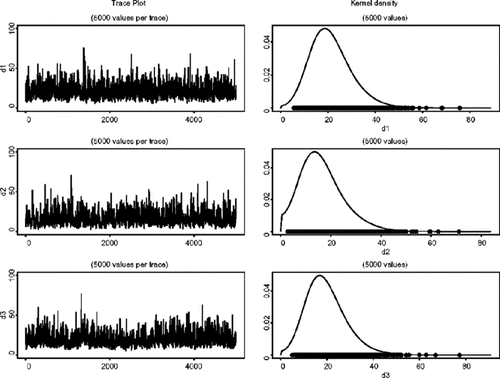
ν的边缘分布的密度估计1，ν 2，和ω在模型（AFactor MSV）。

所有模型的DIC

为了更好地理解模型定义的含义，我们获得了模型（AFactor-t-MSV）和模型（DC-MSV）的波动率和相关性的平滑估计。

结论

在本文中，我们提出通过WinBUGS使用贝叶斯MCMC技术估计和比较多变量SV模型。MCMC是一种功能强大的方法，与其他方法相比具有许多优势。但是，编写用于估计多变量SV模型的第一个MCMC程序并不容易，并且比较替代的多变量SV规范在计算上是复杂的。WinBUGS强加了一个简短而敏锐的学习曲线。在双变量设置中，我们表明其实现简单且计算速度相当快。此外，处理丰富的模型也非常灵活。然而，由于WinBUGS提供Gibbs采样算法，我们发现混合采样通常很慢，因此需要长时间采样。