引言

本节开始，介绍贝叶斯线性回归(Bayesian Linear Regression)。

回顾：线性回归

场景构建

给定数据集合$\mathcal{D}ata={\left\{\left(x^{(i)},y^{(i)}\right)\right\}}_{i=1}^N$，其中样本$x^{(i)}(1=1,2,\cdots ,N)$是$p$维随机变量，对应的标签信息$y^{(i)}$是一维随机变量：
$$\begin{array}{rl}{x}^{(i)}& \in {\mathbb{R}}^p,y^{(i)}\in \mathbb{R}i=1,2,\cdots ,N\\ \mathcal{X}& ={\left(x^{(1)},x^{(2)},\cdots ,x^{(N)}\right)}^T={\left(\begin{array}{c}{x}_1^{(1)},x_2^{(1)},\cdots ,x_p^{(1)}\\ x_1^{(2)},x_2^{(2)},\cdots ,x_p^{(2)}\\ ⋮\\ x_1^{(N)},x_2^{(N)},\cdots ,x_p^{(N)}\end{array}\right)}_{N\times p}\mathcal{Y}=\left(\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ ⋮\\ y_{N\times 1}^{(N)}\end{array}\right)\end{array}$$

从概率密度函数认识最小二乘法

给定数据集合$Data$以及相应拟合直线表示如下：

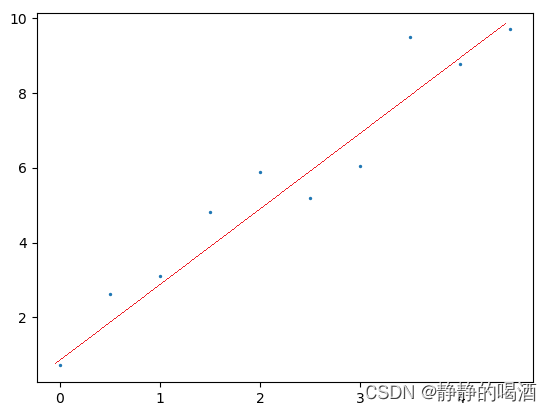
其中直线的表达式为：
这里‘偏置信息’$b$忽略掉,$x_i(i=1,2,\cdots ,p)$表示样本的第$i$维特征信息。
$$f(\mathcal{X})={\mathcal{W}}^T\mathcal{X}={\mathcal{X}}^T\mathcal{W}=\sum _{i=1}^p{w}_i\cdot x_i$$
从概率密度函数角度观察，标签分布可看作是$f(x)$的基础加上均值为0的高斯分布噪声：
$\mathcal{X}$是包含$p$维特征的随机变量集合;$\mathcal{Y}$是一个一维随机变量;$ϵ$表示一维高斯分布(它和$\mathcal{Y}$的维数相同)。
$$\mathcal{Y}=f(\mathcal{X})+ϵ\mathcal{X}\in {\mathbb{R}}^p,\mathcal{Y}\in \mathbb{R},ϵ\sim \mathcal{N}(0,{\sigma }^2)$$

回顾：最小二乘估计

关于线性回归问题求解模型参数$\mathcal{W}$时，使用的是最小二乘估计(Least Square Estimation,LSE)：
$$\mathcal{L}(\mathcal{W})=\sum _{i=1}^N||{\mathcal{W}}^T{x}^{(i)}-y^{(i)}|{|}^2$$
并且通过最小二乘估计，求解模型参数$\mathcal{W}$的矩阵形式表达：
矩阵表达的弊端：

• ${\mathcal{X}}^T\mathcal{X}$是一个$p\times p$的对称矩阵，它至少是半正定矩阵，但不一定是正定矩阵。从而导致$({\mathcal{X}}^T\mathcal{X}{)}^{-1}$可能是不可求的。
• 由于$\mathcal{X}$是样本集合，如果$\mathcal{X}$的样本量较大，会导致${\mathcal{X}}^T\mathcal{X}$的计算代价极高。
  $$\mathcal{W}=({\mathcal{X}}^T\mathcal{X}{)}^{-1}{\mathcal{X}}^T\mathcal{Y}$$

从概率密度函数角度观察，最小二乘估计本质是极大似然估计(Maximum Likelihood Estimate，MLE)：
给定样本$x^{(i)}$和对应标签$y^{(i)}$之间的关联关系，可以得到$\mathcal{P}(y^{(i)}\mid x^{(i)})$的概率分布：
这里先将$\mu$写在上面。
$$\begin{array}{rl}& y^{(i)}={\mathcal{W}}^T{x}^{(i)}+ϵϵ\sim \mathcal{N}(\mu ,{\sigma }^2)\\ & \to \mathcal{P}(y^{(i)}\mid x^{(i)};\mathcal{W})\sim \mathcal{N}({\mathcal{W}}^T{x}^{(i)}+\mu ,{\sigma }^2)\end{array}$$
对似然函数$\mathcal{L}(\mathcal{W})$进行构建：
将高斯分布的概率密度函数带入~
$$\begin{array}{rl}\mathcal{L}(\mathcal{W})& =\log \prod _{i=1}^N\mathcal{P}(y^{(i)}\mid x^{(i)};\mathcal{W})\\ & =\sum _{i=1}^N\log \left[\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{[y^{(i)}-\left({\mathcal{W}}^T{x}^{(i)}+\mu \right){]}^2}{2{\sigma }^2}\right)\right]\end{array}$$
使用极大似然估计对最优模型参数$\hat{\mathcal{W}}$进行计算：
其中${\sum }_{i=1}^N\log \frac{1}{\sigma \sqrt{2\pi }},\frac{1}{2{\sigma }^2}$均是与$x^{(i)}$无关的量，视作常数。
$$\begin{array}{rl}\hat{\mathcal{W}}& =\underset{\mathcal{W}}{\mathrm{argmax}}\mathcal{L}(\mathcal{W})\\ & =\underset{\mathcal{W}}{\mathrm{argmax}}\left\{\sum _{i=1}^N\log \left[\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{[y^{(i)}-\left({\mathcal{W}}^T{x}^{(i)}+\mu \right){]}^2}{2{\sigma }^2}\right)\right]\right\}\\ & =\underset{\mathcal{W}}{\mathrm{argmax}}\left\{\sum _{i=1}^N\log \frac{1}{\sigma \sqrt{2\pi }}-\sum _{i=1}^N\frac{[y^{(i)}-\left({\mathcal{W}}^T{x}^{(i)}+\mu \right){]}^2}{2{\sigma }^2}\right\}\\ & \propto \underset{\mathcal{W}}{\mathrm{argmin}}\sum _{i=1}^N{\left[y^{(i)}-\left({\mathcal{W}}^T{x}^{(i)}+\mu \right)\right]}^2\\ & \mu =0\to \underset{\mathcal{W}}{\mathrm{argmin}}\sum _{i=1}^N{\left[y^{(i)}-{\mathcal{W}}^T{x}^{(i)}\right]}^2\end{array}$$
这里令$\mu =0$关于极大似然估计关于$\hat{\mathcal{W}}$的求解公式与最小二乘估计相同。

回顾：线性回归与正则化

针对最小二乘估计的过拟合 问题，引入正则化(Regularized)。常见的正则化有两种方式：

• Lasso回归(${\mathcal{L}}_1$正则化)
  $$\underset{\mathcal{W}}{\mathrm{argmin}}\left[\sum _{i=1}^N||{\mathcal{W}}^T{x}^{(i)}-y^{(i)}|{|}^2+\lambda ||\mathcal{W}|{|}_1\right]||\mathcal{W}|{|}_1=|w_1|+\cdots +|w_p|$$
• 岭回归(Ridge回归；${\mathcal{L}}_2$正则化)
  $$\underset{\mathcal{W}}{\mathrm{argmin}}\left[\sum _{i=1}^N||{\mathcal{W}}^T{x}^{(i)}-y^{(i)}|{|}^2+\lambda ||\mathcal{W}|{|}_2^2\right]||\mathcal{W}|{|}_2^2=\sqrt{|w_1{|}^2+\cdot +|w_p{|}^2}$$

从概率密度函数角度考虑基于正则化的最小二乘估计，可将其视作关于$\mathcal{W}$的最大后验概率估计(Maximum a Posteriori Probability,MAP)：
$$\begin{array}{rl}{\hat{\mathcal{W}}}_{MAP}& =\underset{\mathcal{W}}{\mathrm{argmax}}\frac{\mathcal{P}(\mathcal{Y}\mid \mathcal{W})\cdot \mathcal{P}(\mathcal{W})}{\mathcal{P}(\mathcal{Y})}\\ & \propto \underset{\mathcal{W}}{\mathrm{argmax}}P(\mathcal{Y}\mid \mathcal{W})\cdot \mathcal{P}(\mathcal{W})\end{array}$$
由于样本间独立同分布，因而有：
增加一个$\log$函数，不影响最值的取值结果。
$${\hat{\mathcal{W}}}_{MAP}\propto \underset{\mathcal{W}}{\mathrm{argmax}}\left[\log \prod _{i=1}^N\mathcal{P}(y^{(i)}\mid \mathcal{W})\cdot \mathcal{P}(\mathcal{W})\right]$$
令先验分布$\mathcal{P}(\mathcal{W})\sim \mathcal{N}({\mu }_0,{\sigma }_0^2)$，将$\mathcal{P}(\mathcal{Y}\mid \mathcal{W})\sim \mathcal{N}({\mathcal{W}}^T\mathcal{X},{\sigma }^2)$一同代入上式，有：
这里既包含对$\mathcal{W}$分布的假设。也包含关于高斯噪声$\mathcal{Y}\mid \mathcal{W}$的假设。该假设完全写法是$\mathcal{Y}\mid \mathcal{X};\mathcal{W}$只不过这里$\mathcal{X}$是已知量，省略掉了。
$${\hat{\mathcal{W}}}_{MAP}=\underset{\mathcal{W}}{\mathrm{argmin}}\sum _{i=1}^N\left[{\left(y^{(i)}-{\mathcal{W}}^T{x}^{(i)}\right)}^2+\frac{{\sigma }^2}{{\sigma }_0^2}(\mathcal{W}-{\mu }_0{)}^2\right]$$
令$\lambda =\frac{{\sigma }^2}{{\sigma }_0^2},{\mu }_0=0$时，上式将转化为：
$${\hat{\mathcal{W}}}_{MAP}=\underset{\mathcal{W}}{\mathrm{argmin}}\sum _{i=1}^N\left[{\left(y^{(i)}-{\mathcal{W}}^T{x}^{(i)}\right)}^2+\lambda ||\mathcal{W}|{|}_2^2\right]$$
上述是关于岭回归$\mathcal{W}$分布的假设，如果是Lasso回归，将$\mathcal{W}$分布假设为拉普拉斯分布(Laplace Distribution)。

关于线性回归的简单小结

无论是最小二乘估计还是包含了正则化的最小二乘估计，其本质均是频率派的求解方式，将模型参数$\mathcal{W}$视作未知常量，通过极大似然估计、最大后验概率估计等方式对$\mathcal{W}$进行优化，从而使目标函数达到最值。
本质上是‘优化问题’。

并且这种估计方式是点估计(Point Estimation)，由于概率模型能够源源不断的生成样本，理论上无法完美地、精确描述概率模型的分布信息，只能通过有限的样本集合来估计模型参数。
也就是说，使用‘统计得到的样本集合’估计总体参数。
假设某概率模型服从高斯分布：$\mathcal{N}(\mu ,{\sigma }^2)$，这里的$\mu ,{\sigma }^2$是描述概率分布的参数，是固定的。但是该概率模型可以生成无穷无尽的样本，假设某样本集合$\mathcal{X}=\left\{x^{(1)},x^{(2)},\cdots ,x^{(N)}\right\}$是生成出的一部分样本，我们通过统计的方式得到该样本的均值、方差${\mu }_{\mathcal{X}},{\sigma }_{\mathcal{X}}^2$去估计真正的参数$\mu ,{\sigma }^2$。

贝叶斯线性回归

区别于频率派的点估计方式，贝叶斯派使用的是贝叶斯估计(Bayesian Estimation)。此时的参数$\mathcal{W}$不再是一个未知的常量，而是一个随机变量。

对于$\mathcal{W}$的估计过程中，需要通过给定数据估计出$\mathcal{W}$的后验概率分布$\mathcal{P}(\mathcal{W}\mid Data)$。

贝叶斯方法

在变分推断——基本介绍中介绍过贝叶斯学派角度认识问题。其核心是：不同于频率派将模型参数$\mathcal{W}$看作未知的常量，而是将$\mathcal{W}$看作随机变量，从而求解$\mathcal{W}$的后验概率分布$\mathcal{P}(\mathcal{W}\mid Data)$，基于该分布，对新样本进行预测：
令新样本为$\hat{x}$,预测任务可表示为$\mathcal{P}(\hat{x}\mid Data)$.
$$\begin{array}{rl}\mathcal{P}(\hat{x}\mid Data)& ={\int }_{\mathcal{W}\mid Data}\mathcal{P}(\hat{x},\mathcal{W}\mid Data)d\mathcal{W}\\ & ={\int }_{\mathcal{W}\mid Data}\mathcal{P}(\mathcal{W}\mid \mathcal{X})\cdot \mathcal{P}(\hat{x}\mid \mathcal{W})d\mathcal{W}\\ & ={\mathbb{E}}_{\mathcal{W}\mid Data}\left[\mathcal{P}(\hat{x}\mid \mathcal{W})\right]\end{array}$$

贝叶斯方法在线性回归中的任务

针对上述贝叶斯方法的描述，在线性回归中的任务包含以下两个：

• 推断任务(Inference)：通过贝叶斯定理，求解后验概率$\mathcal{P}(\mathcal{W}\mid Data)$。
• 预测任务(Prediction)：基于后验概率$\mathcal{P}(\mathcal{W}\mid Data)$，对新样本的后验$\mathcal{P}(\hat{x}\mid Data)$进行估计。

贝叶斯线性回归推断任务介绍

后验概率$\mathcal{P}(\mathcal{W}\mid Data)$表示如下：
数据集合$Data$包含样本集合$\mathcal{X}$和对应标签集合$\mathcal{Y}$.
$$\begin{array}{rl}\mathcal{P}(\mathcal{W}\mid Data)& =\mathcal{P}(\mathcal{W}\mid \mathcal{X},\mathcal{Y})\\ & =\frac{\mathcal{P}(\mathcal{W},\mathcal{Y}\mid \mathcal{X})}{\mathcal{P}(\mathcal{Y}\mid \mathcal{X})}\\ & =\frac{\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})\cdot \mathcal{P}(\mathcal{W})}{{\int }_{\mathcal{W}}\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})\cdot \mathcal{P}(\mathcal{W})d\mathcal{W}}\end{array}$$
其中$\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})$是似然(Likelihood)，$\mathcal{P}(\mathcal{W})$是先验分布(Piror Distribution)。
$\mathcal{P}(\mathcal{W})$实际上是$\mathcal{P}(\mathcal{W}\mid \mathcal{X})$,由于$\mathcal{X}$不对$\mathcal{W}$产生影响，这里省略。这个先验分布是推断之前给定的某一种分布。

由于样本之间独立同分布，因而似然$\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})$可表示为如下形式：
根据上面介绍的线性回归模型，样本$x^{(i)}$和对应标签$y^{(i)}$之间是‘包含均值为0高斯噪声的线性关系’：
$$\begin{gathered} \mathcal{P}(y^{(i)}\mid \mathcal{W},x^{(i)})\sim \mathcal{N}({\mathcal{W}}^T{x}^{(i)},{\sigma }^2) \\ \begin{array}{rl}\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})& =\prod _{i=1}^N\mathcal{P}(y^{(i)}\mid \mathcal{W},x^{(i)})\\ & =\prod _{i=1}^N\mathcal{N}({\mathcal{W}}^T{x}^{(i)},{\sigma }^2)\end{array} \end{gathered}$$
关于先验分布$\mathcal{P}(\mathcal{W})$，我们同样假设它是一个 均值为0的高斯分布：
其中${\Sigma }_{prior}$表示先验高斯分布的‘协方差矩阵’，由于$\mathcal{W}$和$\mathcal{X}$维度相同，因而$[{\Sigma }_{prior}{]}_{p\times p}$.
$$\mathcal{P}(\mathcal{W})\sim \mathcal{N}(0,{\Sigma }_{piror})$$
至此，关于$\mathcal{W}$的后验概率分布$\mathcal{P}(\mathcal{W}\mid Data)$可表示为：
贝叶斯定理的分母部分称作’证据‘(Evidence),它可看作关于数据集合$Data$的一个常量(因为数据集合是已知的)，和参数$\mathcal{W}$无关。
$$\begin{array}{rl}\mathcal{P}(\mathcal{W}\mid Data)& =\frac{\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})\cdot \mathcal{P}(\mathcal{W})}{{\int }_{\mathcal{W}}\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})\cdot \mathcal{P}(\mathcal{W})d\mathcal{W}}\\ & \propto \mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})\cdot \mathcal{P}(\mathcal{W})\end{array}$$
观察，由于似然$\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})$服从高斯分布，并且先验分布同样假设为高斯分布，因而后验分布$\mathcal{P}(\mathcal{W}\mid Data)$同样服从高斯分布。

• 这里用到了指数族分布的共轭性质,具体描述是：似然$\mathcal{P}(\mathcal{Y}\mid \mathcal{W},\mathcal{X})$存在一个共轭的先验分布$\mathcal{P}(\mathcal{W})$,对应效果是：后验分布$\mathcal{P}(\mathcal{W}\mid Data)$与先验分布形成相同的分布形式。
• 并且高斯分布是一个包含’自共轭性质‘的指数族分布。即高斯分布是高斯分布自身的’共轭分布‘。

定义后验的高斯分布为$\mathcal{N}({\mu }_{\mathcal{W}},{\Sigma }_{\mathcal{W}})$，具体表示如下：
$$\mathcal{N}({\mu }_{\mathcal{W}},{\Sigma }_{\mathcal{W}})\propto \left[\prod _{i=1}^N\mathcal{N}(y^{(i)}\mid {\mathcal{W}}^T{x}^{(i)},{\sigma }^2)\right]\cdot \mathcal{N}(0,{\Sigma }_{piror})$$

下一节将介绍${\mu }_{\mathcal{W}},{\Sigma }_{\mathcal{W}}$的求解过程。

相关参考：
机器学习-贝叶斯线性回归（1）-背景介绍
机器学习-贝叶斯线性回归（2）-推导介绍