成绩

比赛链接

比赛过程

被虐4h

比赛体验不是很好
我开始五分后才在qq上看到题
第一题签到题
第二题调了1h吧，算法题做的不多，题目没读全，wa了几发，有几发是网络问题，交了显示失败，但还是判wa了
第三题知道是贪心，但是写不出来，
然后看排行榜第四过的人多，就去做第四了，前两个wa也是网络问题，然后我把样例和图片的1~26都模拟出来
但是超时了，然后就无了，坐牢四小时
不过没有这个比赛的话，我也没这种心态俩小时调一个题，

说点有意思的，比赛过程看到别人在qq群里讨论，真的无语，做不出来一直ex别人，我第一反应就是直接把qq关了，做自己就行！！
还是太菜，不过相比今年蓝桥杯的时候，debug的能力有了提升，希望明年蓝桥杯能进国赛吧,继续加油~

放几张图

满怀期待 😃

在这里插入图片描述

超时差最后一个样例qaq
提前去吃饭了，感觉真做不出来了，打表也是TLE

代码

A

签到题

B

B-莲子的机械动力学

题目背景

如果遇到提交失败，请多次刷新，多次提交，会有成功几率

【题目背景和题目描述的两个题面是完全等价的，您可以选择阅读其中一部分。】

专攻超统一物理学的莲子，对机械结构的运动颇有了解。如下图所示，是一个三进制加法计算器的（超简化）示意图。

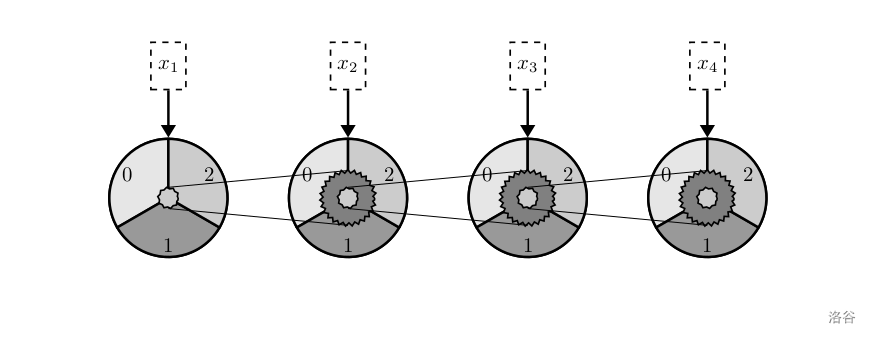
一个四位的三进制整数，从低到高位，标为 $x_1,x_2,x_3,x_4$ 。换言之，这个数可以写成 $\overline{x_4x_3x_2x_1}_{(3)}$ 。把它放在这四个齿轮里，对应箭头指向的数字就是现在这位的数值。

在这种机械式计算机里，我们通过齿轮的啮合来实现数位间的连接。通过不同齿轮半径的比例来确定进制。图中所有浅灰色的小齿轮的半径，比上使用皮带相接的较大齿轮的半径，都是 $1 : 3$ 。那么小齿轮每转动一圈，大齿轮就转动 $\dfrac{1}{3}$ 圈，也就是刚好一个数码的角度。

于是，我们通过控制齿轮的半径实现了 $3$ 进制的进位。

如果需要实现三进制加法，则只需要在对应数位拨动对应的数码长度即可。

如下是个例子，实现 $\overline{1021}_{(3)}+\overline{0021}_{(3)}=\overline{1112}_{(3)}$

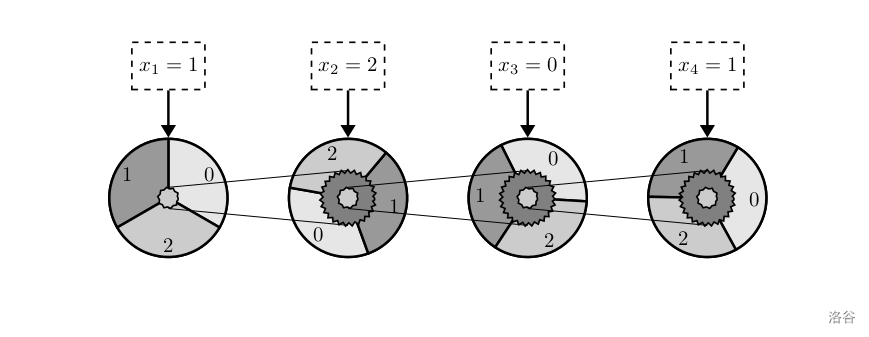
初始时齿轮的状态如上。

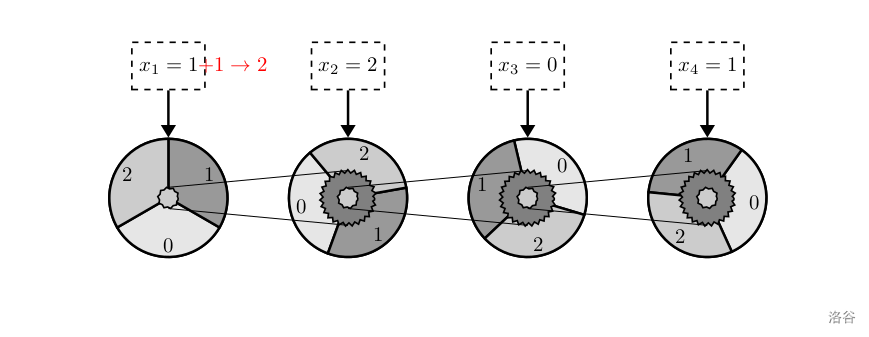
把第一个齿轮拨动一个单位长度，变为如上图所示。

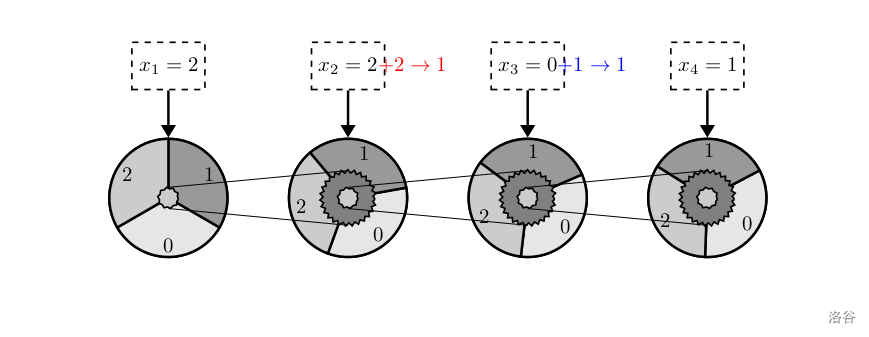
把第二个齿轮拨动两个单位长度，变为如上图所示。读数，得到结果 $\overline{1112}_{(3)}$ 。

现在莲子设计了如下图所示的机械结构。对于从左往右数的第 $i$ 枚齿轮，它上面的浅色小齿轮与第 $i + 1$ 枚齿轮上的深色小齿轮的半径之比为 $1 : (i + 2)$ 。也就是说，第 $i$ 枚齿轮每转动 $1$ 圈，第 $i + 1$ 枚齿轮转过的角度恰好为它上面的一个数码。

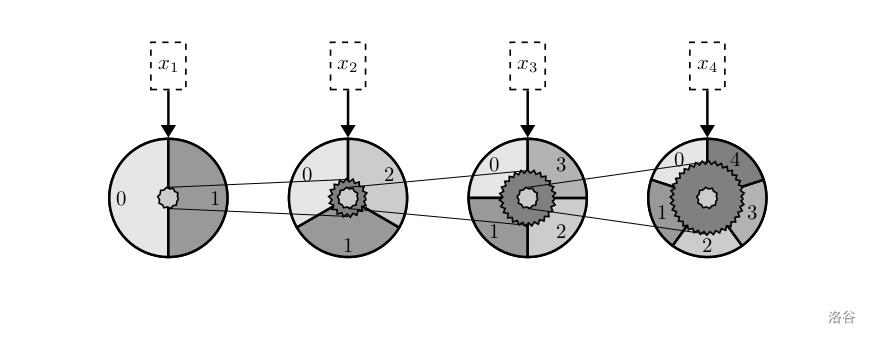
莲子想要知道，在这样的特别的进制表示下，给定 $a, b$ ，那么计算出的 $a + b$ 的结果是多少。

题目描述

题目背景的问题可以转化为如下描述：

给定两个长度分别为 $n, m$ 的整数 $a, b$ ，计算它们的和。

但是要注意的是，这里的 $a, b$ 采用了某种特殊的进制表示法。最终的结果也会采用该种表示法。具体而言，从低位往高位数起，第 $i$ 位采用的是 $i + 1$ 进制。换言之，相较于十进制下每一位的「逢 $10$ 进 $1$ 」，该种进制下第 $i$ 位是「逢 $i + 1$ 进 $1$ 」。

下图所示，左边是十进制的竖式加法；右边是这种特殊进制的竖式加法。图中的红色加号表示上一位发生了进位。

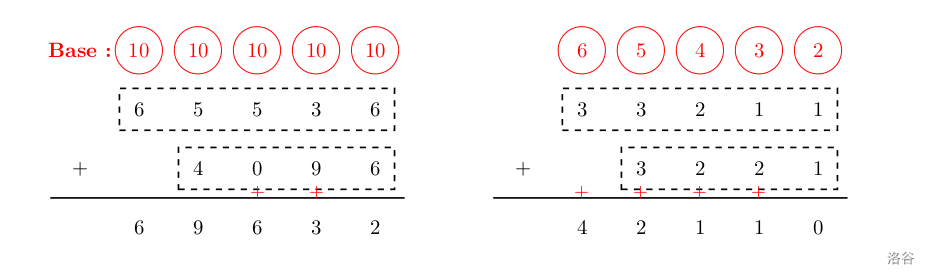
输入格式

第一行有两个整数 $n, m$ ，分别表示 $a$ 和 $b$ 的位数。
第二行有 $n$ 个整数，中间用空格隔开，从高到低位描述 $a$ 的每个数码。
第三行有 $m$ 个整数，中间用空格隔开，从高到低位描述 $b$ 的每个数码。

输出格式

输出有若干个整数，从高到低位输出 $a + b$ 在这种特殊表示法下的结果。

样例 #1

样例输入 #1

5 4
3 3 2 1 1
3 2 2 1

样例输出 #1

4 2 1 1 0

样例 #2

样例输入 #2

10 1
10 9 8 7 6 5 4 3 2 1
0

样例输出 #2

10 9 8 7 6 5 4 3 2 1

提示

对于全部数据，保证 $1\le n,m\le 2\times 10^5$ ，从低位往高位数起有 $a_i\in[0,i]$ ， $b_i\in[0,i]$ 。请使用 Java 或 Python 语言作答的选手注意输入输出时的效率。

D

E-梅莉的市场经济学

题目背景

梅莉这个学期选修了经济学。但是主修心理学的她实在不擅长经济领域的分析，为此她时常抱怨自己学不会，想退课。

但是如果现在退掉的话这学期的学分就不够啦，因此她根据“梦中”的经历，“胡诌”了一个简单到不现实的市场模型，并依据这个模型编起了 essay。为了方便地编出图表，她需要写一个程序来查询每个时刻的市场贸易差。

题目描述

市场每一天的贸易差可以视为一个有周期性规律的数列 $a$ ： $\color{red}[0],\color{blue}[0,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak 0],\color{red}[0,\allowbreak 1,\allowbreak 2,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak -2,\allowbreak -1,\allowbreak 0],\allowbreak \color{blue}[0,\allowbreak 1,\allowbreak 2,\allowbreak 3,\allowbreak 2,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak -2,\allowbreak -3,\allowbreak -2,\allowbreak -1,\allowbreak 0]\dots$ 具体而言， $a$ 可以被分为无穷段，第 $i$ 段的内容为 $\{0,\allowbreak 1,\allowbreak \cdots,\allowbreak i,\allowbreak i-1,\allowbreak \cdots,0,\allowbreak -1,\allowbreak \cdots,\allowbreak -i,\allowbreak -i+1,\allowbreak \cdots 0\}$ 。如下图所示，是将 $a$ 数列内的前一些点绘制在坐标轴上的情况：

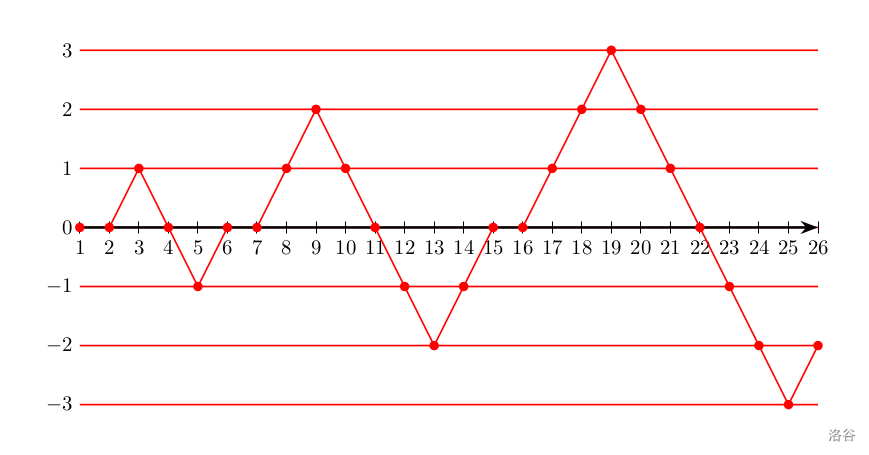
现在梅莉对市场发起了 $q$ 次询问，每次她会给定一个 $k$ ，希望求出 $a_k$ 是多少。

输入格式

第一行有一个正整数 $q$ ，表示询问次数。
接下来 $q$ 行，每行一个正整数 $k$ ，描述每次询问。

输出格式

输出共 $q$ 行。对于每次询问，输出对应的结果。

样例 #1

样例输入 #1

样例输出 #1

提示

对于所有数据， $\leq q \leq 10^5$ ， $\leq k \leq 4\times 10^{18}$ 。

打表也试了，一样tle
应该不是模拟

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
    #define rep(i, a, n) for(int i = a; i <= n; i ++)
    #define per(i, a, n) for(int i = n; i <= a; i --)
    #define pb push_back;
    #define fs first;
    #define sz second;
    #include <stdlib.h> // atoi
    #define debug cout<<"debug"<<"\n"
    #define endl "\n";
    const int INF = 0x3f3f3f3f;
    const int mod=1e9+7;
    
    const int N = 4e18 + 10;


    // struct node {
    //     ll maa,mii,dd;
    // } pa[N];

    vector<pair<ll,ll>> pa(N);

    void solve () {
        ll x;
        cin >> x;
        ll ma,mi;
        ll d = 1;
        ll tmp = 1;
        if(x == 1) {
            cout << 0 << endl;
            return;
        }
        int i = 1;
        while(1) {
            mi = d;
            if(i % 2 ==  0) {
                d += 4 * tmp;
                tmp ++;
            }else {
                d += 1;
            }
            ma = d;
            if(d > x) {
                // cout << i << endl;
                // cout << mi << ' ' << ma << endl;
                d = i / 2;
                
            }
            i ++;
        }
      
      
        // cout << d << endl;
        // d /= 2;
        // cout  << d << endl;
        long long mid = (mi + ma) / 2;
        long long mmid = 0;
        // cout << x << " ";
        if(x == mid  || x == ma || x == mi) {
            cout << 0 << endl;
            return;
        }
        if(x > mid) {
            mmid = (ma + mid) / 2;
            if(x == mmid) {
                cout << d*(-1) << endl;
                return ;
            } else if(x > mmid){
                while(x != mmid) {
                    x --;
                    d --;
                }
                cout << d * (- 1) << endl;
                return ;
            } else {
                while(x != mmid) {
                    x ++;
                    d --;
                }
                cout << d * (-1)<< endl;
                return ;
            }
        } else {
            mmid = (mi + mid) / 2;
            // cout << "--  " << endl;
            if(x == mmid) {
                cout << d << endl;
                return ;
            } else if(x > mmid){
                while(x != mmid) {
                    x --;
                    d --;
                    // cout <<
                }
                cout << d << endl;
                return ;
            } else {
                while(x != mmid) {
                    x ++;
                    d --;
                }
                cout << d << endl;
                return ;
            }
        }


        return ;
    }

    int main(void){
        ll x = N;
        ll ma,mi;
        ll d = 1;
        ll tmp = 1;
        int i = 1;
        while(1) {
            mi = d;
            if(i % 2 ==  0) {
                d += 4 * tmp;
                tmp ++;
            }else {
                d += 1;
            }
            ma = d;
            // pa[i] = {mi,ma};
            // pa[x] = 
            if(d > 1000)break;
            i ++;
        }
        cout << 1 << endl;
        // cout << pa[1].second/ << pa[1].first;
        // for(auto &it : pa) {
        //     cout << it.first <<' ' << it.second << endl;
        // }
    	// freopen("C:\\Users\\27285\\Desktop\\hcpc\\c--primer\\cppz\\AC\\hcpc\\in.txt","r",stdin);
        ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
        // int T = 1;
        // cin >> T;
        // while(T --) solve();
        return 0;
    }