二分每次折半，倍增每次2的倍数

原理先存储每个小区间的最值也就是初始化，之后直接查询

1. 把数列按倍增分成小区间

对数列的每个元素，把从它开始的数列分成长度为1、2、4、8、…的小区间。下图给出了一个分区的例子，它按小区间的长度分成了很多组。

• 第 1 组是长度为 1 的小区间，有 n 个小区间，每个小区间有 1 个元素；
• 第 2 组是长度为 2 的小区间，有 n 个小区间，每个小区间有 2 个元素；
• 第 3 组是长度为 4 的小区间，有 n 个小区间，每个小区间有 4 个元素；
• ...共有 logn (2为底)组。

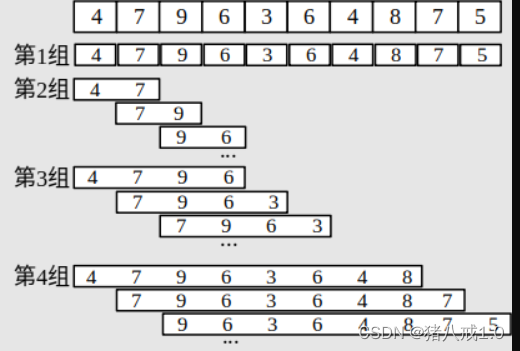
每组的小区间的最值，可以从前一组递推而来。例如第 3 组 {4, 7, 9, 6} 的最值，可以从第 2 组 {4, 4,7}、{9,6} 的最值递推得到。

所以我们定义 dp[s][k]，表示左端点是 s，区间长度为 2^k 的区间最值。它的递推关系是：（1<<(k-1) 等于 2^{k-1}）

所以：dp[s][k]=min(dp[s][k−1],dp[s+1<<(k−1)][k−1])

dp[s][k]当前组，是由后面两组推导出来的

图中的每一组都需计算 n 次，共 logn组，总计算量是 O(nlogn)。

2.查询

查询区间[L,R]的最值,L是左端点，R是右端点，区间长度len=R-L+1，区间长度为 2^k 的最值2^k=len

所以k=log(R-L+1)  (2为底,注意Java中的Math.log(n)是以e为底）

如果以10为底的话 k=log(R-L+1)/log(2.0)           (换底公式）

最后给出区间 [L, R]最小值的计算公式，等于覆盖它的两个小区间的最小值：

min(dp[L][k],dp[R−(1<<k)+1][k]);             （1<<k也就是2^k)

3.题目练习

https://www.lanqiao.cn/problems/1205/learning/

区间最大值

给定一个长度为 N 的数组 a，其值分别为 a1,a2,...,aN 
现有 Q 个询问，每个询问包含一个区间，请回答该区间的最大值为多少。

输入描述
输入第 1行包含两个正整数 N,Q，分别表示数组 a的长度和询问的个数。

第 2 行包含 N 个非负整数 a1,a2,...,aN ，表示数组 a 元素的值。

后面每行表示一个询问，每个询问包含两个整数 L,R，表示区间的左右端点

1<=N,Q<=5*10^5   -10^9<=ai<=10^9
输出描述
输出共 Q 行，每行包含一个整数，表示相应询问的答案。

输入输出样例
示例 1
输入

5 5
1 2 3 4 5
1 1 
1 2 
1 3
3 4
2 5

输出

1
2
3
4
5

import java.util.Scanner;

public class Main {
	static int N=500000;
	static int n,m;
	static int L,R;
	static int a[]=new int[N];
	//第二个参数是k 设为40即可，也可其他
	static int dp_max[][]=new int[N][40];
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n=sc.nextInt();
		m=sc.nextInt();
		for(int i=1;i<=n;i++) {
			a[i]=sc.nextInt();
		}
		st_init();
		for(int j=1;j<=m;j++){		
	        L=sc.nextInt();
	        R=sc.nextInt();	  
	        System.out.println(st_query(L,R));
	    }
		
	}


	// 把数列按倍增分成小区间
	public static void st_init(){
	    for(int i=1;i<=n;i++)   //初始化区间长度为1时的值
	        dp_max[i][0]=a[i];  
	    	int p=(int)(Math.log10(n)/Math.log10(2.0));     
	    
	    for(int k=1;k<=p;k++) //倍增计算小区间。先算小区间，再算大区间，逐步递推
	        for(int s=1;s+(1<<k)<=n+1;s++)
	            dp_max[s][k]=Math.max(dp_max[s][k-1], dp_max[s+(1<<(k-1))][k-1]);
	}
	//查询
	public static int st_query(int L,int R){
		int k =(int)(Math.log10(R-L+1)/Math.log10(2.0));           
	    return Math.max(dp_max[L][k],dp_max[R-(1<<k)+1][k]);
	}
}

https://www.lanqiao.cn/problems/1375/learning/

同理

import java.util.Scanner;

public class Main {
	static int N=500000;
	static int n,m;
	static int L,R;
	static int a[]=new int[N];
	//第二个参数是k 设为40即可，也可其他
	static int dp_min[][]=new int[N][40];
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		n=sc.nextInt();
		m=sc.nextInt();
		for(int i=1;i<=n;i++) {
			a[i]=sc.nextInt();
		}
		st_init();
		for(int i=1;i<=n-m+1;i++){		
	        System.out.println(st_query(i,i+m-1));
	    }
		
	}


	// 把数列按倍增分成小区间
	public static void st_init(){
	    for(int i=1;i<=n;i++)   //初始化区间长度为1时的值
	        dp_min[i][0]=a[i];  
	    	int p=(int)(Math.log10(n)/Math.log10(2.0));     
	    
	    for(int k=1;k<=p;k++) //倍增计算小区间。先算小区间，再算大区间，逐步递推
	        for(int s=1;s+(1<<k)<=n+1;s++)
	            dp_min[s][k]=Math.min(dp_min[s][k-1], dp_min[s+(1<<(k-1))][k-1]);
	}
	//查询
	public static int st_query(int L,int R){
		int k =(int)(Math.log10(R-L+1)/Math.log10(2.0));           
	    return Math.min(dp_min[L][k],dp_min[R-(1<<k)+1][k]);
	}
}