Problem - C - Codeforces

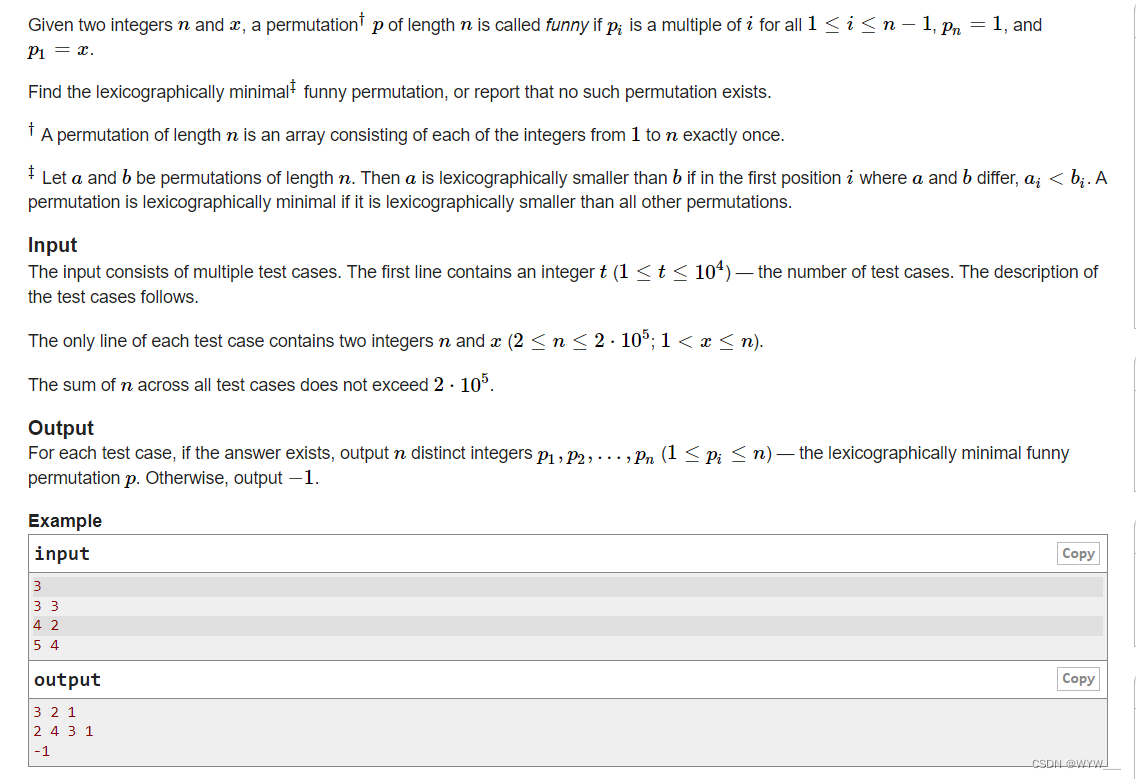
给定两个整数n和x，如果pi是i的倍数，所有1≤i≤n-1，pn=1，且p1=x，则长度为n的排列组合† p被称为搞笑。

找出最小的有趣的排列组合，或报告说不存在这样的排列组合。

† 长度为n的排列组合是一个由1到n的每个整数精确地组成的数组。

‡ 让a和b是长度为n的排列组合。如果在a和b不同的第一个位置i，ai<bi，则a在词典上小于b。如果一个排列组合比其他所有的排列组合都小，那么这个排列组合就是词典上最小的排列组合。

输入
输入由多个测试案例组成。第一行包含一个整数t（1≤t≤104）--测试案例的数量。测试用例的描述如下。

每个测试用例的唯一一行包含两个整数n和x（2≤n≤2⋅105；1<x≤n）。

所有测试用例的n之和不超过2⋅105。

输出
对于每个测试用例，如果答案存在，则输出n个不同的整数p1,p2,...,pn(1≤pi≤n) - 词汇学上最小的有趣的排列组合p，否则，输出-1。

例子
输入复制
3
3 3
4 2
5 4
输出拷贝
3 2 1 
2 4 3 1 
-1
注意
在第一个测试案例中，排列组合[3,2,1]满足所有条件：p1=3, p3=1, 并且。

p1=3是1的倍数。
p2=2是2的倍数。
在第二个测试案例中，排列组合[2,4,3,1]满足所有条件：p1=2，p4=1，并且。

P1=2是1的倍数。
p2=4是2的倍数。
p3=3是3的倍数。
我们可以证明，这些排列组合是lexicographically最小的。

在第三个测试案例中不存在这样的排列组合。

题解:
我们目前知道

a[1] = x

a[n] = 1

如果n不能放在x的位置上,则一定不存在这样的数组

如果存在

a[x] = n

但是可能会出现,

t = x(代表目前a[t] = n)

if(n%(x*i) == 0&&x*i%t == 0)

swap(a[x*i],a[t])

t = x*i

那么我们就可以把小的数往前提,大的数往后放,模拟这个过程即可

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<map>
#include<vector>
#include<queue>
using namespace std;
#define int long long
//1 1 3 3 3
int n,k,m;
int a[200040];
void solve()
{
	int n,x;
	cin >> n >> x;
	if(n%x)
	{
		cout<<"-1\n";
	}
	else
	{
		for(int i =2 ;i < n;i++)
		a[i] = i;
		a[x] = n;
		a[1] = x;
		a[n] = 1;
		int t = x;
		for(int i = 1;i*x < n;i++)
		{
			if(n%(i*x) == 0&& (x*i)%t == 0)
			{
				swap(a[i*x],a[t]);
				t = i*x;
			}
		}
		for(int i = 1;i <= n;i++)
		cout<<a[i]<<" ";
		cout<<"\n";
	}
}
signed main()
{
	int t = 1;
	cin >> t;
	while(t--)
	{
		solve();
	}
}
//4 8 12 16 20 24
//

//1 2 3 2
//1 2 2 2 2 3
//