ROC-AUC曲线（分类模型）

混淆矩阵

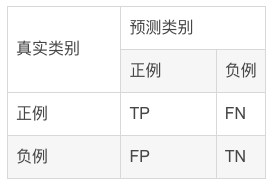
混淆矩阵中所包含的信息

• True negative(TN)，称为真阴率，表明实际是负样本预测成负样本的样本数（预测是负样本，预测对了）
• False positive(FP)，称为假阳率，表明实际是负样本预测成正样本的样本数（预测是正样本，预测错了）
• False negative(FN)，称为假阴率，表明实际是正样本预测成负样本的样本数（预测是负样本，预测错了）
• True positive(TP)，称为真阳率，表明实际是正样本预测成正样本的样本数（预测是正样本，预测对了）
  ROC曲线示例
  

可以看到，ROC曲线的纵坐标为真阳率true positive rate（TPR）（也就是recall），横坐标为假阳率false positive rate（FPR）。
TPR即真实正例中对的比例，FPR即真实负例中的错的比例。

• 真正类率(True Postive Rate)TPR:
  TPR=TP/(TP+FN)
  代表分类器 预测为正类中实际为正实例占所有正实例 的比例。
• 假正类率(False Postive Rate)FPR:
  FPR=FP/(FP+TN)
  代表分类器 预测为正类中实际为负实例 占 所有负实例 的比例。
  

可以看到，右上角的阈值最小，对应坐标点(1,1)；左下角阈值最大，对应坐标点为(0,0)。从右上角到左下角，随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。

• 横轴FPR: FPR越大，预测正类中实际负类越多。
• 纵轴TPR：TPR越大，预测正类中实际正类越多。
• 理想目标：TPR=1，FPR=0，即图中(0,1)点，此时ROC曲线越靠拢(0,1)点，越偏离45度对角线越好。

AUC值是什么？

AUC（Area Under Curve）被定义为ROC曲线下与坐标轴围成的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。

• AUC越接近1.0，检测方法真实性越高;
• 等于0.5时，则真实性最低，无应用价值。
  

ROC曲线绘制的代码实现

#导入库
from sklearn.metrics import confusion_matrix,accuracy_score,f1_score,roc_auc_score,recall_score,precision_score,roc_curve
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
  
#绘制roc曲线   
def calculate_auc(y_test, pred):
    print("auc:",roc_auc_score(y_test, pred))
    fpr, tpr, thersholds = roc_curve(y_test, pred)
    roc_auc = auc(fpr, tpr)
    plt.plot(fpr, tpr, 'k-', label='ROC (area = {0:.2f})'.format(roc_auc),color='blue', lw=2)
    plt.xlim([-0.05, 1.05])
    plt.ylim([-0.05, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('ROC Curve')
    plt.legend(loc="lower right")
    plt.plot([0, 1], [0, 1], 'k--')
    plt.show()

相关性热图

表示数据之间的相互依赖关系。但需要注意，数据具有相关性不一定意味着具有因果关系。

相关系数（Pearson）

相关系数是研究变量之间线性相关程度的指标，而相关关系是一种非确定性的关系，数据具有相关性不能推出有因果关系。相关系数的计算公式如下：

其中，公式的分子为X，Y两个变量的协方差，Var(X)和Var(Y)分别是这两个变量的方差。当X,Y的相关程度最高时，即X,Y趋近相同时，很容易发现分子和分母相同，即r=1。

代码实现

相关性计算

import numpy as np
import pandas as pd
# compute correlations
from scipy.stats import spearmanr, pearsonr
from scipy.spatial.distance import cdist

def calc_spearman(df1, df2):
	df1 = pd.DataFrame(df1)
	df2 = pd.DataFrame(df2)
    n1 = df1.shape[1]
    n2 = df2.shape[1]
    corr0, pval0 = spearmanr(df1.values, df2.values)
    # (n1 + n2) x (n1 + n2)
    corr = pd.DataFrame(corr0[:n1, -n2:], index=df1.columns, columns=df2.columns)
    pval = pd.DataFrame(pval0[:n1, -n2:], index=df1.columns, columns=df2.columns)
    return corr, pval

def calc_pearson(df1, df2):
	df1 = pd.DataFrame(df1)
	df2 = pd.DataFrame(df2)
    n1 = df1.shape[1]
    n2 = df2.shape[1]
    corr0, pval0 = np.zeros((n1, n2)), np.zeros((n1, n2))
    for row in range(n1):
        for col in range(n2):
            _corr, _p = pearsonr(df1.values[:, row], df2.values[:, col])
            corr0[row, col] = _corr
            pval0[row, col] = _p
    # n1 x n2
    corr = pd.DataFrame(corr0, index=df1.columns, columns=df2.columns)
    pval = pd.DataFrame(pval0, index=df1.columns, columns=df2.columns)
    return corr, pval

画出相关性图

import matplotlib.pyplot as plt
import seaborn as sns

def pvalue_marker(pval, corr=None, only_pos=False):
    if only_pos:  # 只标记正相关
        if corr is None:  
            print('correlations `corr` is not provided, '
                  'negative correlations cannot be filtered!')
        else:
            pval = pval + (corr < 0).astype(float)
    pval_marker = pval.applymap(lambda x: '**' if x < 0.01 else ('*' if x < 0.05 else ''))
    return pval_marker

def plot_heatmap(
    mat, cmap='RdBu_r', 
    xlabel=f'column', ylabel=f'row',
    tt='',
    fp=None,
    **kwds
):
    fig, ax = plt.subplots()
    sns.heatmap(mat, ax=ax, cmap=cmap, cbar_kws={'shrink': 0.5}, **kwds)
    ax.set_title(tt)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if fp is not None:
        ax.figure.savefig(fp, bbox_inches='tight')
    return ax

实例

#构造有一定相关性的随机矩阵
df1 = pd.DataFrame(np.random.randn(40, 9))
df2 = df1.iloc[:, :-1] + df1.iloc[:, 1: ].values * 0.6
df2 += 0.2 * np.random.randn(*df2.shape)

#绘图
corr, pval = calc_pearson(df1, df2)
pval_marker = pvalue_marker(pval, corr, only_pos=only_pos)
tt = 'Spearman correlations'
plot_heatmap(
    corr, xlabel='df2', ylabel='df1',
    tt=tt, cmap='RdBu_r', #vmax=0.75, vmin=-0.1,
    annot=pval_marker, fmt='s',
)

only_pos 这个参数为 False 时, 会同时标记显著的正相关和负相关.
cmap属性调整颜色可选参数：

‘Accent’, ‘Accent_r’, ‘Blues’, ‘Blues_r’, ‘BrBG’, ‘BrBG_r’, ‘BuGn’, ‘BuGn_r’, ‘BuPu’, ‘BuPu_r’, ‘CMRmap’,‘CMRmap_r’, ‘Dark2’, ‘Dark2_r’, ‘GnBu’, ‘GnBu_r’, ‘Greens’, ‘Greens_r’, ‘Greys’, ‘Greys_r’, ‘OrRd’, ‘OrRd_r’, ‘Oranges’, ‘Oranges_r’, ‘PRGn’, ‘PRGn_r’, ‘Paired’, ‘Paired_r’, ‘Pastel1’, ‘Pastel1_r’, ‘Pastel2’, ‘Pastel2_r’, ‘PiYG’, ‘PiYG_r’, ‘PuBu’, ‘PuBuGn’, ‘PuBuGn_r’, ‘PuBu_r’, ‘PuOr’, ‘PuOr_r’, ‘PuRd’, ‘PuRd_r’, ‘Purples’, ‘Purples_r’, ‘RdBu’, ‘RdBu_r’, ‘RdGy’, ‘RdGy_r’, ‘RdPu’, ‘RdPu_r’, ‘RdYlBu’, ‘RdYlBu_r’, ‘RdYlGn’, ‘RdYlGn_r’, ‘Reds’, ‘Reds_r’, ‘Set1’, ‘Set1_r’, ‘Set2’, ‘Set2_r’, ‘Set3’, ‘Set3_r’, ‘Spectral’, ‘Spectral_r’, ‘Wistia’, ‘Wistia_r’, ‘YlGn’, ‘YlGnBu’, ‘YlGnBu_r’, ‘YlGn_r’, ‘YlOrBr’, ‘YlOrBr_r’, ‘YlOrRd’, ‘YlOrRd_r’, ‘afmhot’, ‘afmhot_r’, ‘autumn’, ‘autumn_r’, ‘binary’, ‘binary_r’,‘bone’, ‘bone_r’, ‘brg’, ‘brg_r’, ‘bwr’, ‘bwr_r’, ‘cividis’, ‘cividis_r’, ‘cool’, ‘cool_r’, ‘coolwarm’, ‘coolwarm_r’, ‘copper’, ‘copper_r’, ‘crest’, ‘crest_r’, ‘cubehelix’, ‘cubehelix_r’, ‘flag’, ‘flag_r’, ‘flare’, ‘flare_r’, ‘gist_earth’, ‘gist_earth_r’, ‘gist_gray’, ‘gist_gray_r’, ‘gist_heat’, ‘gist_heat_r’, ‘gist_ncar’, ‘gist_ncar_r’, ‘gist_rainbow’, ‘gist_rainbow_r’, ‘gist_stern’, ‘gist_stern_r’, ‘gist_yarg’, ‘gist_yarg_r’, ‘gnuplot’, ‘gnuplot2’, ‘gnuplot2_r’, ‘gnuplot_r’, ‘gray’, ‘gray_r’, ‘hot’, ‘hot_r’, ‘hsv’, ‘hsv_r’,‘plasma’, ‘plasma_r’, ‘prism’, ‘prism_r’, ‘rainbow’, ‘rainbow_r’, ‘rocket’, ‘rocket_r’, ‘seismic’, ‘seismic_r’, ‘spring’, ‘spring_r’, ‘summer’, ‘summer_r’, ‘tab10’, ‘tab10_r’, ‘tab20’, ‘tab20_r’, ‘tab20b’, ‘tab20b_r’, ‘tab20c’, ‘tab20c_r’, ‘terrain’, ‘terrain_r’, ‘turbo’, ‘turbo_r’, ‘twilight’, ‘twilight_r’, ‘twilight_shifted’, ‘twilight_shifted_r’, ‘viridis’, ‘viridis_r’, ‘vlag’, ‘vlag_r’, ‘winter’, ‘winter_r’

棒棒糖图

条形图在数据可视化里，是一个经常被使用到的图表。虽然很好用，也还是存在着缺陷呢。比如条形图条目太多时，会显得臃肿，不够直观。
棒棒糖图表则是对条形图的改进，以一种小清新的设计，清晰明了表达了我们的数据。

代码实现

# 导包
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# 创建数据
x=range(1,41)
values=np.random.uniform(size=40)

# 绘制
plt.stem(x, values)
plt.ylim(0, 1.2)
plt.show()

# stem function: If x is not provided, a sequence of numbers is created by python:
plt.stem(values)
plt.show()

# Create a dataframe
df = pd.DataFrame({'group':list(map(chr, range(65, 85))), 'values':np.random.uniform(size=20) })

# Reorder it based on the values:
ordered_df = df.sort_values(by='values')
my_range=range(1,len(df.index)+1)
ordered_df.head()

# Make the plot
plt.stem(ordered_df['values'])
plt.xticks( my_range, ordered_df['group'])
plt.show()

# Horizontal version
plt.hlines(y=my_range, xmin=0, xmax=ordered_df['values'], color='skyblue')
plt.plot(ordered_df['values'], my_range, "D")

plt.yticks(my_range, ordered_df['group'])
plt.show()

# change color and shape and size and edges
(markers, stemlines, baseline) = plt.stem(values)
plt.setp(markers, marker='D', markersize=10, markeredgecolor="orange", markeredgewidth=2)
plt.show()

# custom the stem lines
(markers, stemlines, baseline) = plt.stem(values)
plt.setp(stemlines, linestyle="-", color="olive", linewidth=0.5 )
plt.show()

# Create a dataframe
value1=np.random.uniform(size=20)
value2=value1+np.random.uniform(size=20)/4
df = pd.DataFrame({'group':list(map(chr, range(65, 85))), 'value1':value1 , 'value2':value2 })

# Reorder it following the values of the first value:
ordered_df = df.sort_values(by='value1')
my_range=range(1,len(df.index)+1)

# The horizontal plot is made using the hline function
plt.hlines(y=my_range, xmin=ordered_df['value1'], xmax=ordered_df['value2'], color='grey', alpha=0.4)
plt.scatter(ordered_df['value1'], my_range, color='skyblue', alpha=1, label='value1')
plt.scatter(ordered_df['value2'], my_range, color='green', alpha=0.4 , label='value2')
plt.legend()

# Add title and axis names
plt.yticks(my_range, ordered_df['group'])
plt.title("Comparison of the value 1 and the value 2", loc='left')
plt.xlabel('Value of the variables')
plt.ylabel('Group')

# Show the graph
plt.show()

# Data
x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x) + np.random.uniform(size=len(x)) - 0.2

# Create a color if the y axis value is equal or greater than 0
my_color = np.where(y>=0, 'orange', 'skyblue')

# The vertical plot is made using the vline function
plt.vlines(x=x, ymin=0, ymax=y, color=my_color, alpha=0.4)
plt.scatter(x, y, color=my_color, s=1, alpha=1)

# Add title and axis names
plt.title("Evolution of the value of ...", loc='left')
plt.xlabel('Value of the variable')
plt.ylabel('Group')

# Show the graph
plt.show()

火山图

火山图（Volcano plots）是散点图的一种，根据变化幅度（FC，Fold Change）和变化幅度的显著性（P value）进行绘制，其中标准化后的FC值作为横坐标，P值作为纵坐标，可直观的反应高变的数据点，常用于基因组学分析（转录组学、代谢组学等）。

绘制

制作差异分析结果数据框

genearray = np.asarray(pvalue)
 
result = pd.DataFrame({'pvalue':genearray,'FoldChange':fold})
 
result['log(pvalue)'] = -np.log10(result['pvalue'])

制作火山图的准备工作

result['sig'] = 'normal'
 
result['size']  =np.abs(result['FoldChange'])/10
 
result.loc[(result.FoldChange> 1 )&(result.pvalue < 0.05),'sig'] = 'up'
result.loc[(result.FoldChange< -1 )&(result.pvalue < 0.05),'sig'] = 'down'

ax = sns.scatterplot(x="FoldChange", y="log(pvalue)",
                      hue='sig',
                      hue_order = ('down','normal','up'),
                      palette=("#377EB8","grey","#E41A1C"),
                      data=result)
ax.set_ylabel('-log(pvalue)',fontweight='bold')
ax.set_xlabel('FoldChange',fontweight='bold')