前向传播与反向传播意义及其参数的更新方式

一、前言

因为本身非科班出身，数学又学的很差，一直都是傻瓜式地用tensorflow和pytorch搭网络。前一段时间竞赛的时候尝试着用简单神经网络做了个题，同学突然问起反向传播的具体原理，一时语塞，遂下决心把这个问题搞明白。这篇学习笔记将以我的认知顺序也就是由浅至深的顺序叙述，里面可能涉及到一些神经网络的基础知识，比如学习率、激活函数、损失函数等，详情可以看看这里，本文不再赘述

写文章的时候查阅了一些资料，感觉写得最好的是这篇文章，我的一些思路也有所参考，推荐去看看，记得给大佬点star : )

二、前反向传播的作用

这个问题应该大部分接触过神经网络的人都有所了解，我最开始的认知也就停留在这一步

前向传播，也叫正向传播，其实就是参数在神经网络中从输入层到输出层的传输过程

反向传播，其实就是根据输出层的输出与实际值的差距，更新神经网络中参数的过程

而一次正向传播加上一次反向传播就是一次网络的学习

话虽如此，参数在网络中到底是如何变化的呢

三、前向传播

首先我们来看一个神经网络，这个神经网络是如此的简单，这种简单结构的网络可以使我们更好地理解神经网络的工作方式。

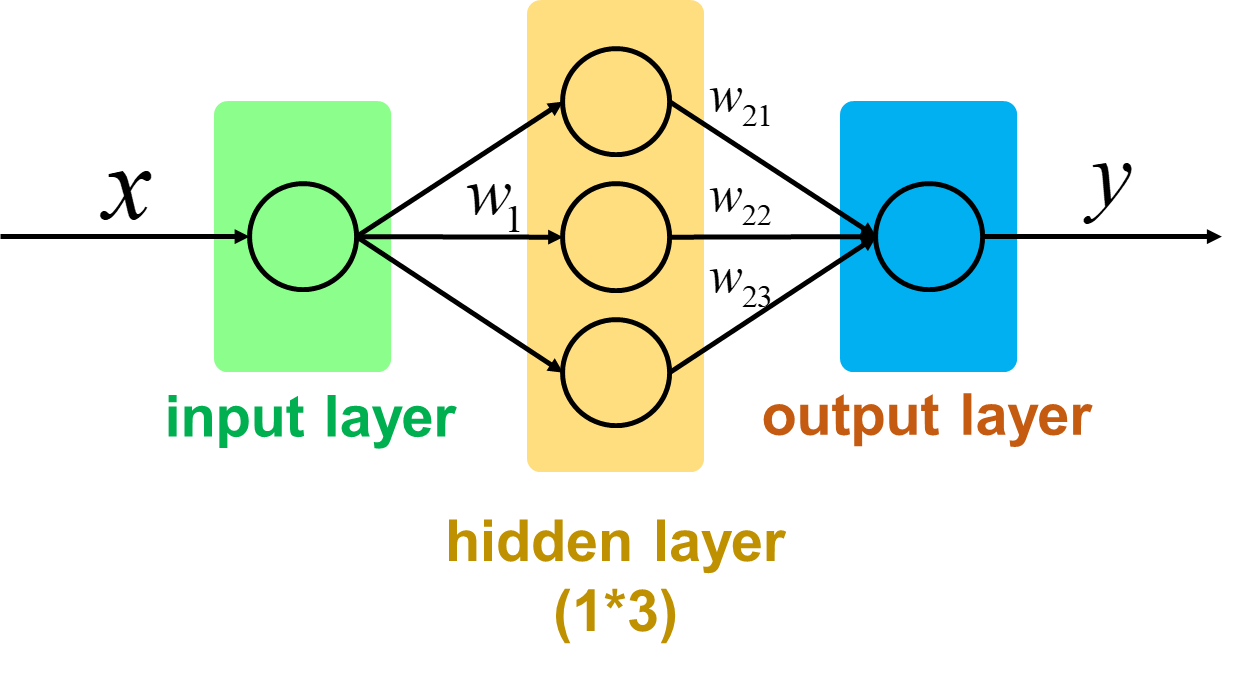
所谓前向传播，其实就是将神经网络的上一层作为下一层的输入，并计算下一层的输出，一直到输出层位置

如上图，假如输入层输入x，那么参数前向传播到隐藏层其实就是输入x与权重矩阵相乘加上偏置项之和再通过激活函数，假设我们使用的激活函数为
$$f(x)=x\times 2$$
此时输入层的输出就是
$$f(x\times w_1+b_1)=(x\times w_1+b_1)\times 2$$
当参数继续向前传播，通过隐藏层的输出到输出层，其值为
$$\sum f(f(x\times w_1+b_1)\times w_2+b_2)=2\times (2\times (w_{1}x+b_1)\times w_2+b_2)（w2和b2是一个1\ast 3的向量，比较复杂，就不展开了）$$
上面的式子的值其实就是神经网络的输出了，这样两个算式描述了一次前向传播的全部过程

四、反向传播

由于反向传播涉及到导数运算，而我的数学能力已经退化到小学水平了，所以这里我们直接使用一个1 * 1 * 1的 “神经网络” 来做演示

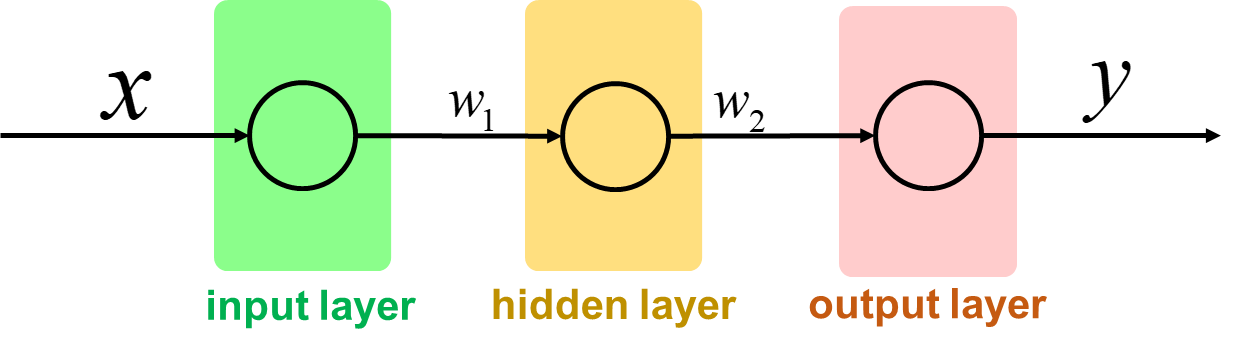
这里我们的损失函数选择使用最常见的均方误差（MSE），即定义损失值为预测值与实际值的差的平方除以样本数，这个损失函数对异常值比较敏感，适用于回归问题
$$LOSS=MSE(y_{\_},y)=\frac{{\sum }_{i=1}^n{(y-y_{\_})}^2}{n}$$
而更新参数的依据，就是使最后预测的结果朝着损失函数值减小的方向移动，故我们用损失函数对每一个参数求偏导，让各个参数往损失函数减小的方向变化。假设我们这里的激活函数为
$$f(x)=x$$

损失函数对各参数求偏导的结果如下
$$定义输入层为输出为h_1，隐藏层输出为h_2，y预测值为y_{\_}$$
$$\frac{\partial L}{\partial y}=2(y_{\_}-y)//单样本情况下，n=1$$
$$\frac{\partial L}{\partial w_2}=\frac{\partial L}{\partial y}\times \frac{\partial y}{\partial h_2}\times \frac{\partial h_2}{\partial w_2}=2(y_{\_}-y)\times 1\times h_1=2(y_{\_}-y)\times 1\times (w_{1}x+b_1)$$
$$\frac{\partial L}{\partial b_2}=\frac{\partial L}{\partial y}\times \frac{\partial y}{\partial h_2}\times \frac{\partial h_2}{\partial b_2}=2(y_{\_}-y)\times 1\times 1=2(y_{\_}-y)$$
$$\frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial y}\times \frac{\partial y}{\partial h_2}\times \frac{\partial h_2}{\partial h_1}\times \frac{\partial h_1}{\partial w_1}=2(y_{\_}-y)\times 1\times w_2\times x$$

$$\frac{\partial L}{\partial b_1}=\frac{\partial L}{\partial y}\times \frac{\partial y}{\partial h_2}\times \frac{\partial h_2}{\partial h_1}\times \frac{\partial h_1}{\partial b_1}=2(y_{\_}-y)\times 1\times w_2\times 1$$

反向传播算法建立在梯度下降法的基础上，已经算出各参数偏导的情况下，需要使用梯度下降法进行参数更新，我们以学习率为μ为例，各参数的更新如下

$$\Delta w_2=-\mu \frac{\partial L}{\partial w_2}\Delta LOSS=-\mu \times 2(y_{\_}-y)\times 1\times (w_{1}x+b_1))\times (y_{\_}-y)$$

$$\Delta b_2=-\mu \frac{\partial L}{\partial b_2}\Delta LOSS=-\mu \times 2(y_{\_}-y)\times (y_{\_}-y)$$

$$\Delta w_1=-\mu \frac{\partial L}{\partial w_1}\Delta LOSS=-\mu \times 2(y_{\_}-y)\times w_2\times x\times (y_{\_}-y)$$

$$\Delta b_1=-\mu \frac{\partial L}{\partial b_1}\Delta LOSS=-\mu \times 2(y_{\_}-y)\times w_2\times (y_{\_}-y)$$

为什么这里要引入学习率的概念呢，有一篇博客非常形象的说明了这个问题，感兴趣的可以看看原文，省流量的可以看下面这个表格，这个表格说明了当学习率等于1的时候可能遇到的困境

轮数	当前轮参数值	梯度x学习率	更新后参数值
1	5	2x5x1=10	5-10=-5
2	-5	2x-5x1=-10	-5-(-10)=5
3	5	2x5x1=10	5-10=-5

很明显，这里参数没有更新，输出结果就像大禹治水，三过家门而不入，训练也就毫无意义

代码

自己懒得写了，在网上找了一个，出处：CSDN
其实这个代码还挺难找的，各位也知道现在CSDN的内容环境，可以用一拖四来形容，但这部分代码写的挺不错，已经向原作者征求使用许可了，但作者现在还没回，如果他的回复是不同意，我会删除这部分代码再自己写一个

import numpy as np
import matplotlib.pyplot as plt

# 激活函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))
 
# 向前传递
def forward(X, W1, W2, W3, b1, b2, b3):
    # 隐藏层1
    Z1 = np.dot(W1.T,X)+b1  # X=n*m ,W1.T=h1*n,b1=h1*1,Z1=h1*m
    A1 = sigmoid(Z1)  # A1=h1*m
    # 隐藏层2
    Z2 = np.dot(W2.T, A1) + b2  # W2.T=h2*h1,b2=h2*1,Z2=h2*m
    A2 = sigmoid(Z2)  # A2=h2*m
    # 输出层
    Z3=np.dot(W3.T,A2)+b3  # W3.T=(h3=1)*h2,b3=(h3=1)*1,Z3=1*m
    A3=sigmoid(Z3)  # A3=1*m
 
    return Z1,Z2,Z3,A1,A2,A3
 
# 反向传播
def backward(Y,X,A3,A2,A1,Z3,Z2,Z1,W3,W2,W1):
    n,m = np.shape(X)
    dZ3 = A3-Y # dZ3=1*m
    dW3 = 1/m *np.dot(A2,dZ3.T) # dW3=h2*1
    db3 = 1/m *np.sum(dZ3,axis=1,keepdims=True) # db3=1*1
 
    dZ2 = np.dot(W3,dZ3)*A2*(1-A2) # dZ2=h2*m
    dW2 = 1/m*np.dot(A1,dZ2.T) #dw2=h1*h2
    db2 = 1/m*np.sum(dZ2,axis=1,keepdims=True) #db2=h2*1
 
    dZ1 = np.dot(W2, dZ2) * A1 * (1 - A1) # dZ1=h1*m
    dW1 = 1 / m * np.dot(X, dZ1.T)  # dW1=n*h
    db1 = 1 / m * np.sum(dZ1,axis=1,keepdims=True)  # db1=h*m
 
    return dZ3,dZ2,dZ1,dW3,dW2,dW1,db3,db2,db1
 
def costfunction(Y,A3):
    m, n = np.shape(Y)
    J=np.sum(Y*np.log(A3)+(1-Y)*np.log(1-A3))/m
    # J = (np.dot(y, np.log(A2.T)) + np.dot((1 - y).T, np.log(1 - A2))) / m
    return -J
 
# Data = np.loadtxt("gua2.txt")
# X = Data[:, 0:-1]
# X = X.T
# Y = Data[:, -1]
# Y=np.reshape(1,m)
X=np.random.rand(100,200)
n,m=np.shape(X)
Y=np.random.rand(1,m)
n_x=n
n_y=1
n_h1=5
n_h2=4
W1=np.random.rand(n_x,n_h1)*0.01
W2=np.random.rand(n_h1,n_h2)*0.01
W3=np.random.rand(n_h2,n_y)*0.01
b1=np.zeros((n_h1,1))
b2=np.zeros((n_h2,1))
b3=np.zeros((n_y,1))
alpha=0.1
number=10000
for i in range(0,number):
    Z1,Z2,Z3,A1,A2,A3=forward(X,W1,W2,W3,b1,b2,b3)
    dZ3, dZ2, dZ1, dW3, dW2, dW1, db3, db2, db1=backward(Y,X,A3,A2,A1,Z3,Z2,Z1,W3,W2,W1)
    W1=W1-alpha*dW1
    W2=W2-alpha*dW2
    W3=W3-alpha*dW3
    b1=b1-alpha*db1
    b2=b2-alpha*db2
    b3=b3-alpha*db3
    J=costfunction(Y,A3)
    if (i%100==0):
        print(i)
    plt.plot(i,J,'ro')
plt.show()