👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
2.1 准确定位
2.2 不确定性定位
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
参考文献:
[1] S. Papatheodorou, Y. Stergiopoulos, and A. Tzes, Distributed area coverage control with imprecise robot localization, In Proceedings of the 24th Mediterranean Conference on Control and Automation (MED), pp. 214-219, June 21-24, 2016, Athens, Greece
[2] S. Papatheodorou, A. Tzes and K. Giannousakis, Experimental Studies on Distributed Control for Area Coverage using Mobile Robots, In Proceedings of the 25th Mediterranean Conference on Control and Automation (MED), pp. 690-695, July 3-6, 2017, Valletta, Malta
[3] S. Papatheodorou, A. Tzes, K. Giannousakis, and Y. Stergiopoulos, Distributed Area Coverage Control with Imprecise Robot Localization, IEEE Transactions on Automatic Control, ISSN 0018-9286, IEEE [Review pending]
[4] S. Papatheodorou, A. Tzes, and Y. Stergiopoulos, Collaborative Visual Area Coverage, Robotics and Autonomous Systems, ISSN 0921-8890, Volume 92, June 2017, Pages 126–138, Elsevier
[5] S. Papatheodorou and A. Tzes, Cooperative Visual Convex Area Coverage using a Tessellation-free strategy, In Proceedings of the 56th IEEE Conference on Decision and Control (CDC) 2017, December 12-15, 2017, Melbourne, Australia [Accepted]
📚2 运行结果
2.1 准确定位
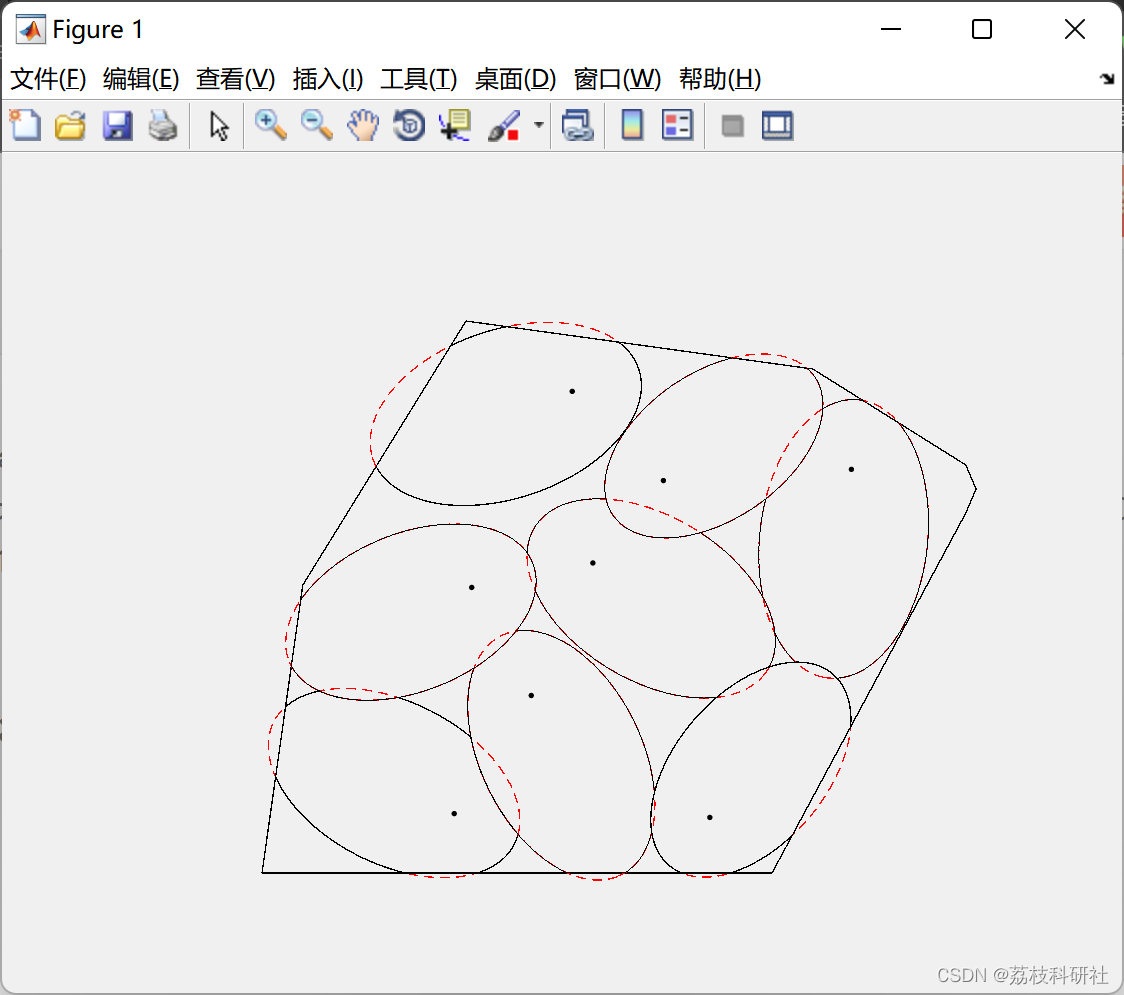
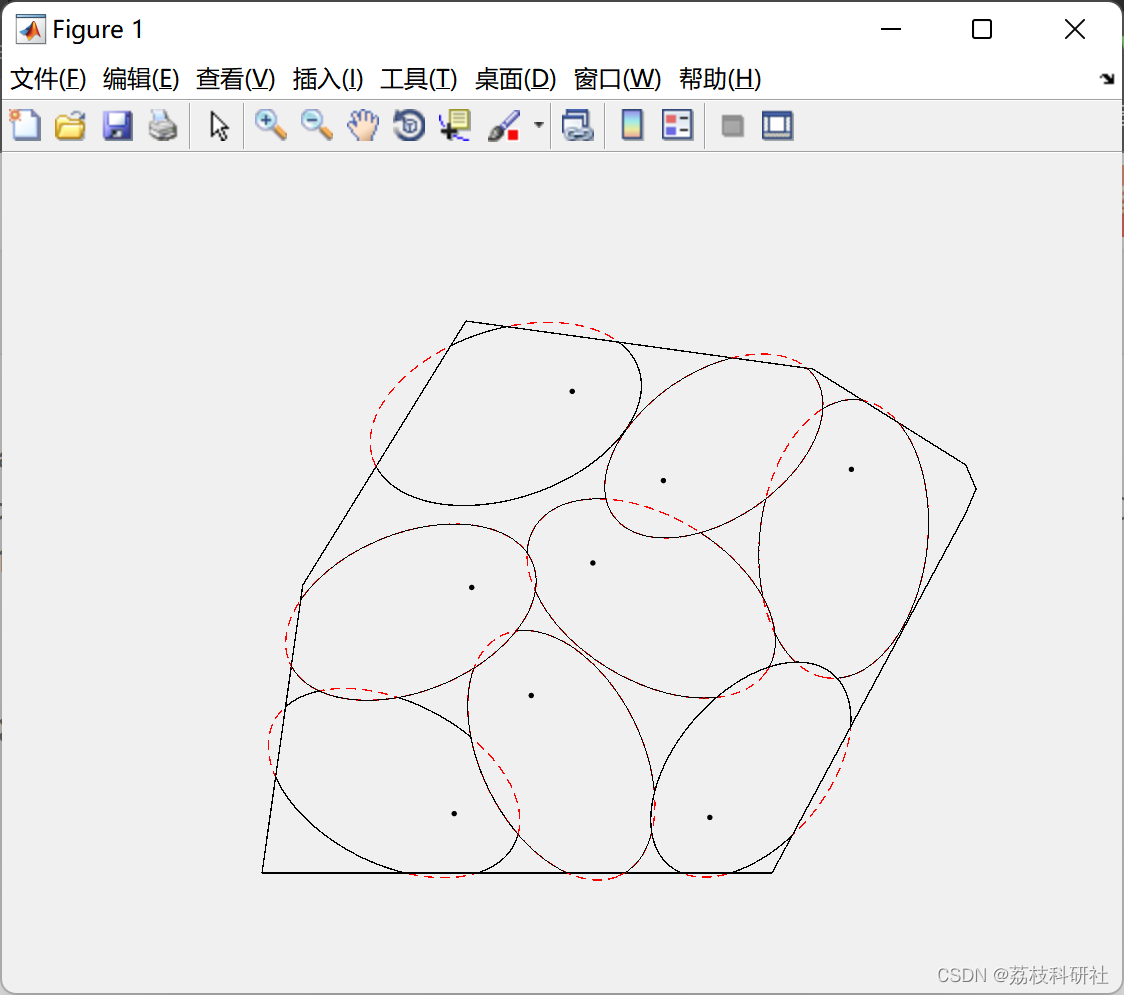
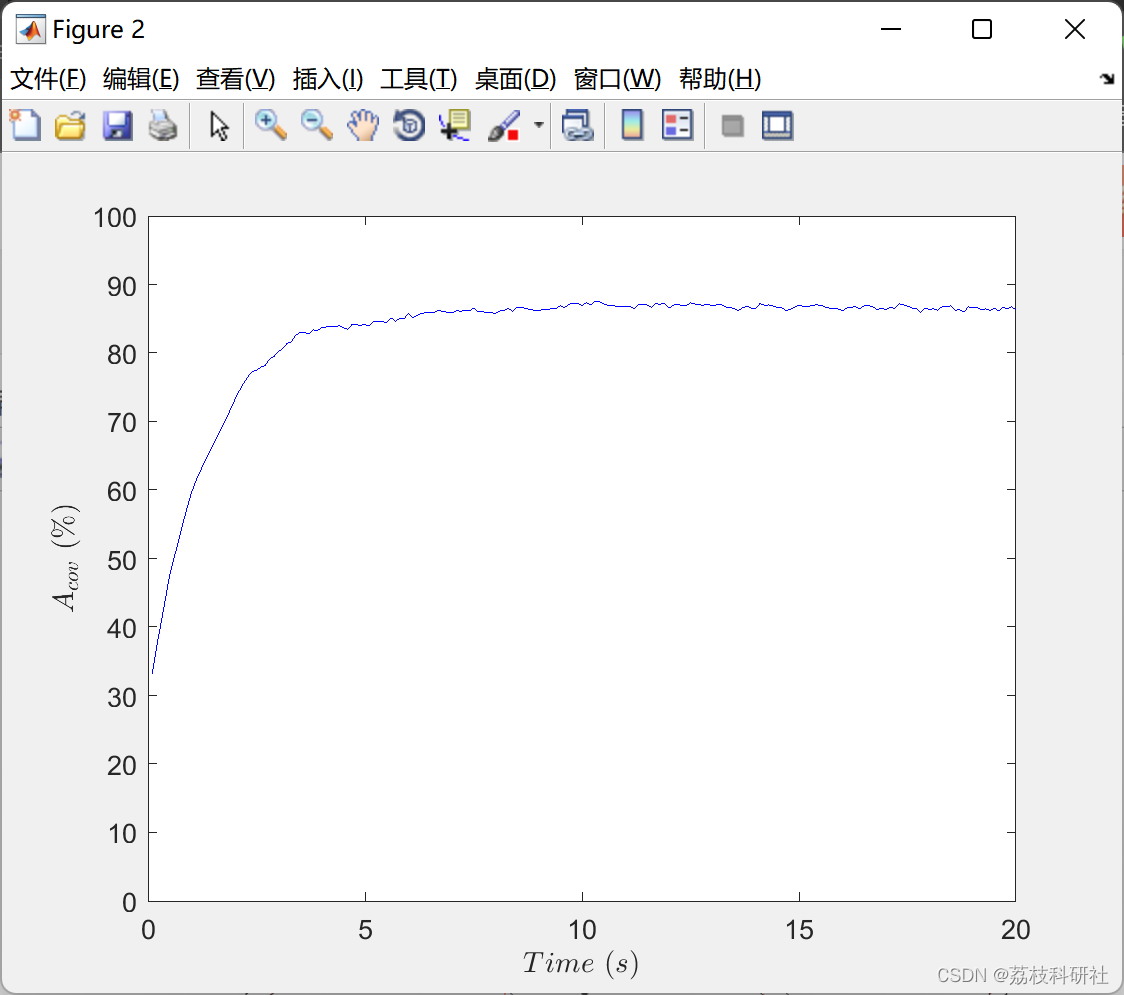
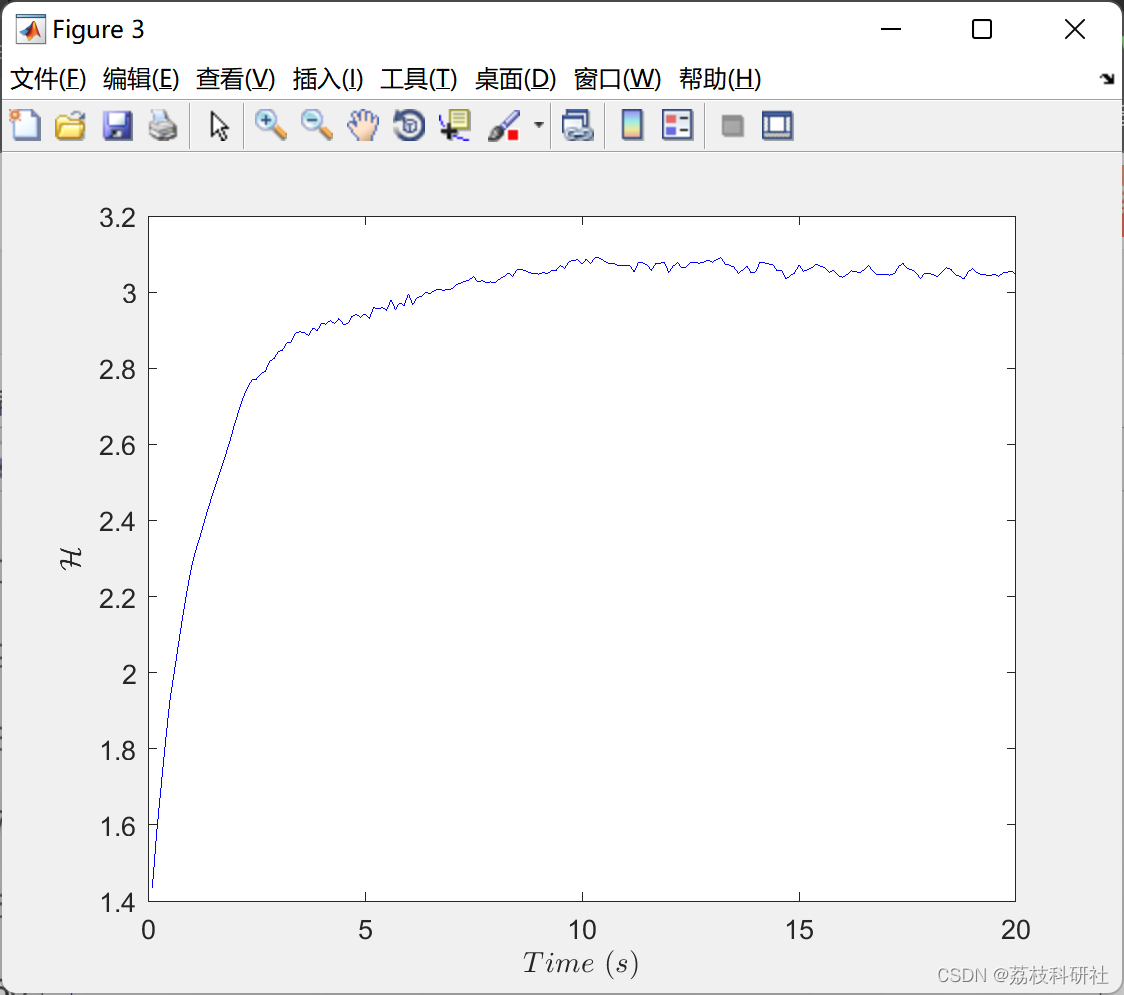
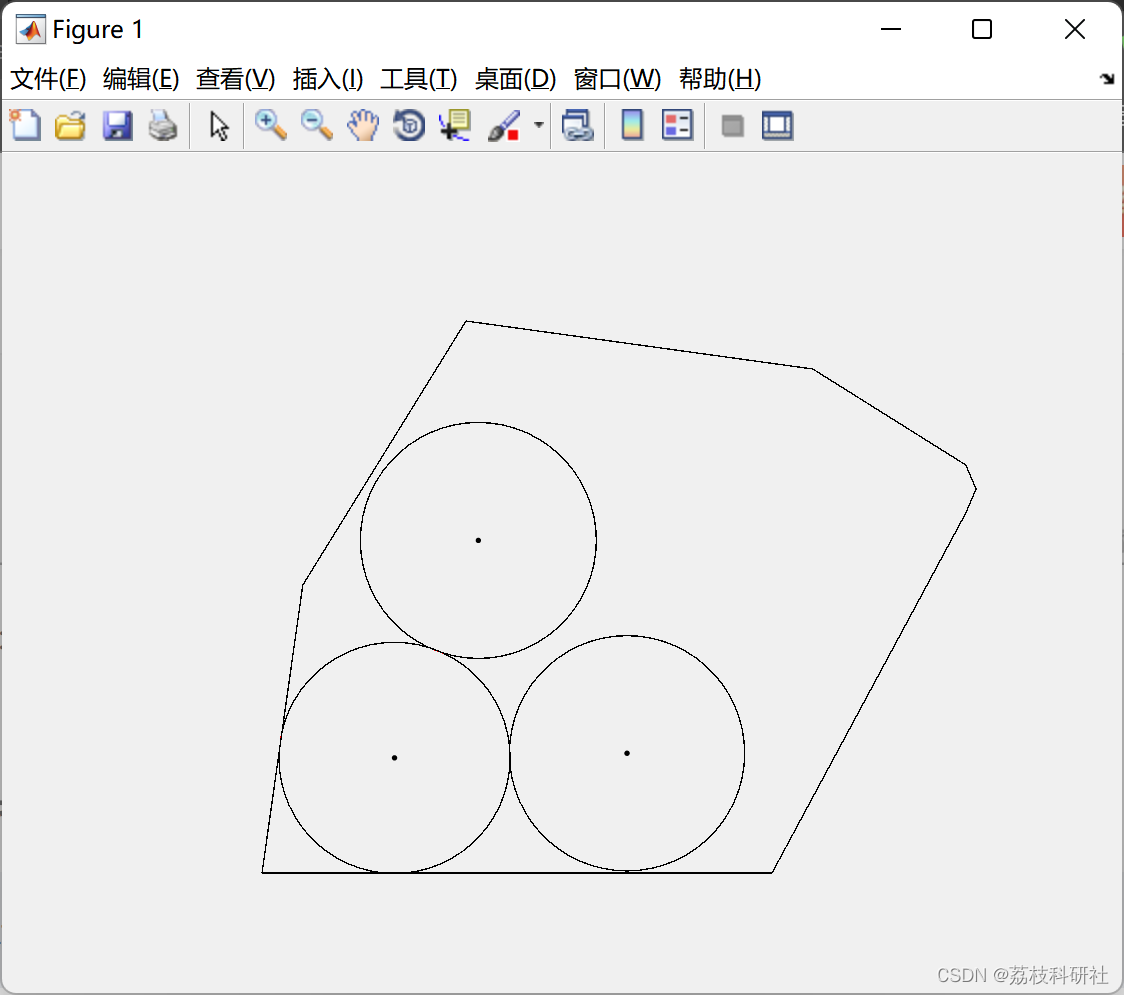
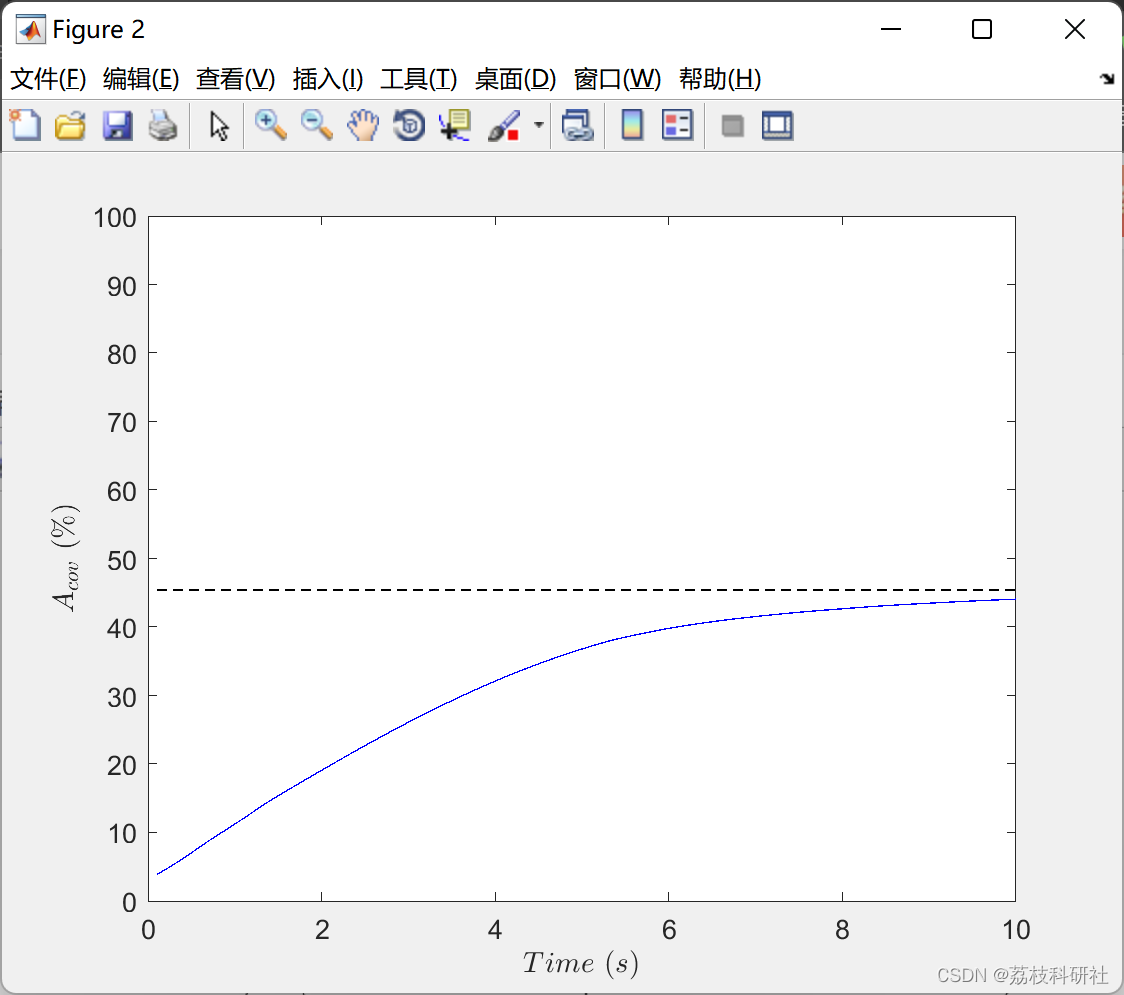
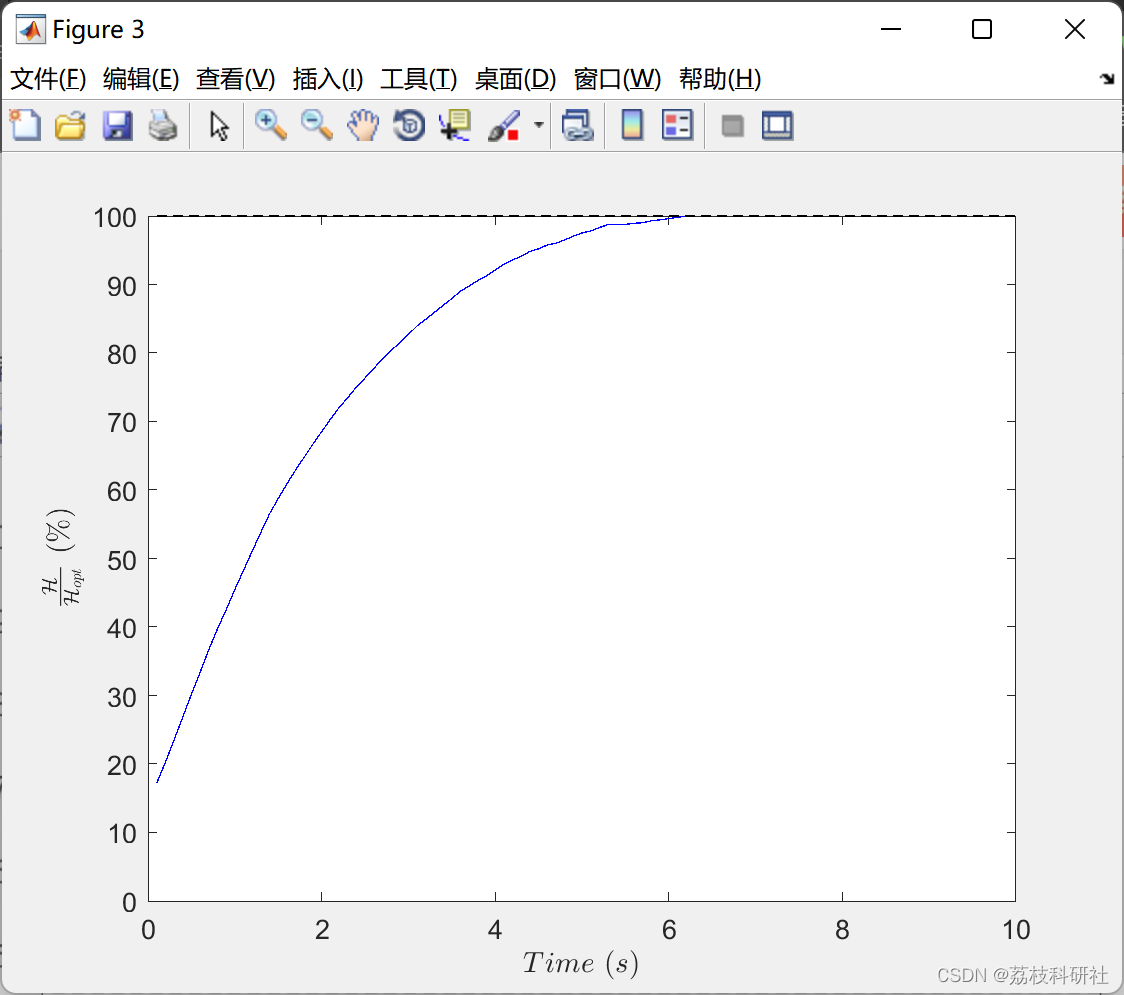
2.2 不确定性定位
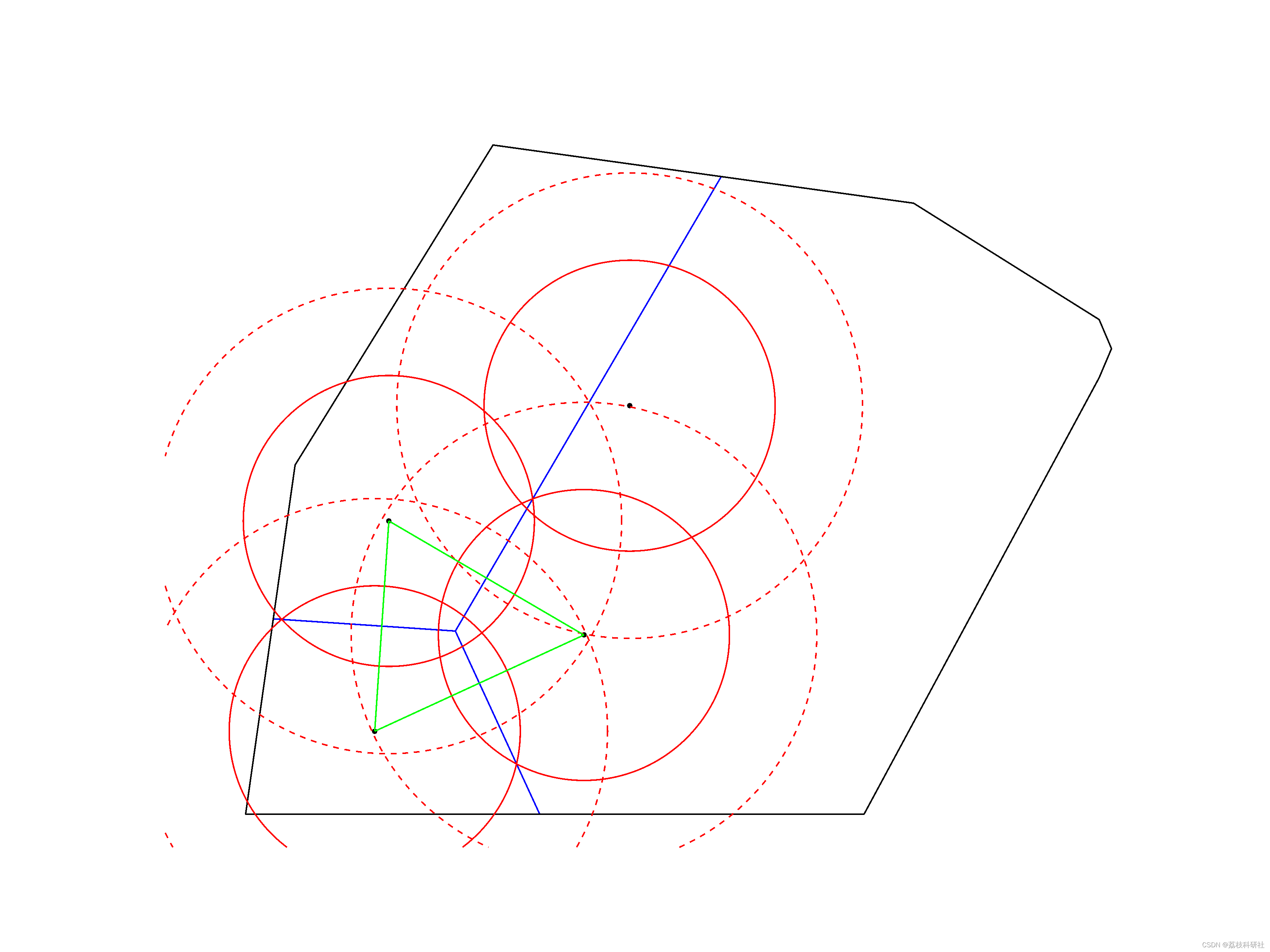
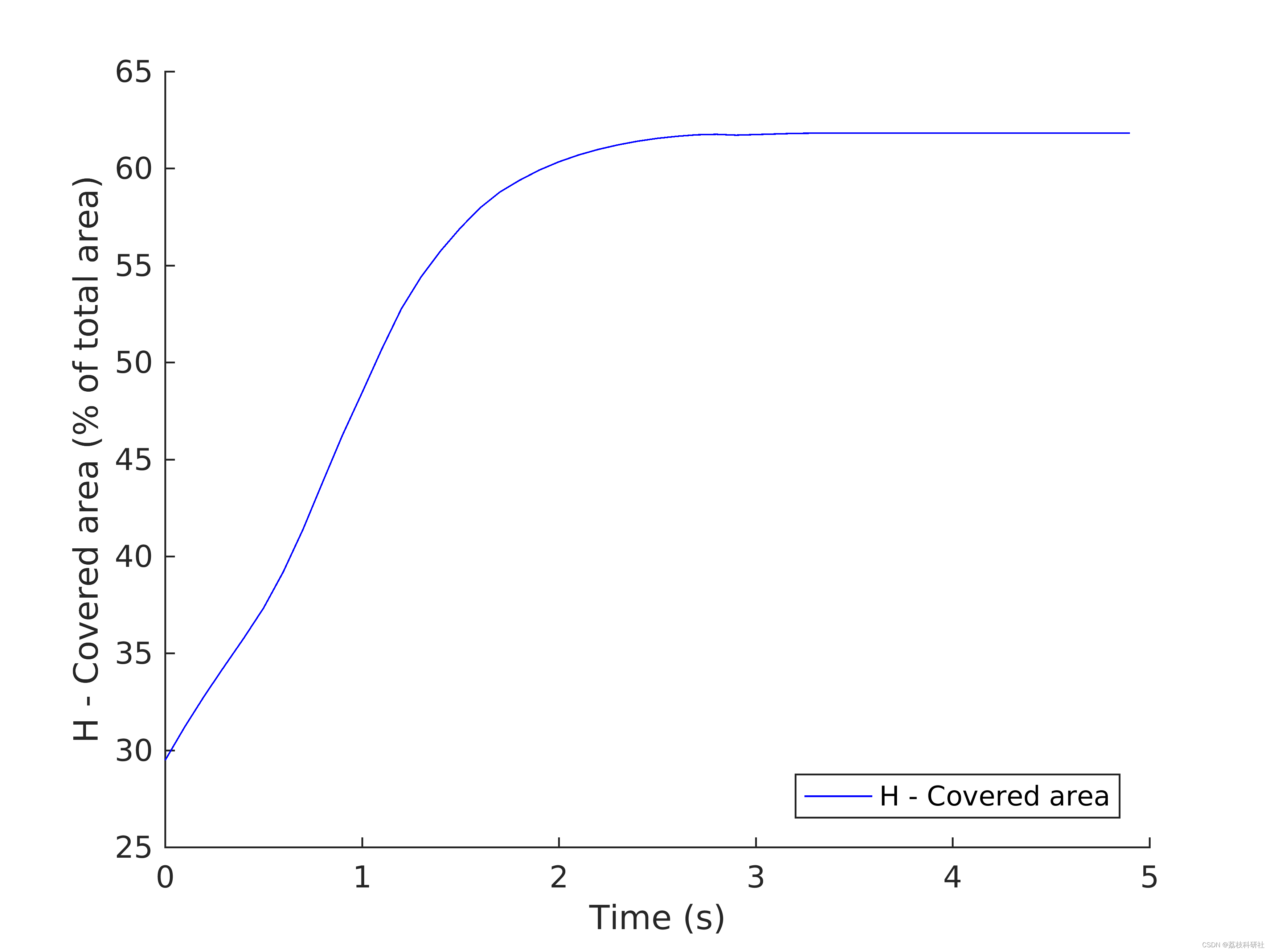
部分代码:
% Translate branches
Hij = Hij + (qi+qj)/2;
Hji = Hji + (qi+qj)/2;
% Jacobian matrices
Jix_xi = diff(Hij(1), xi);
Jix_yi = diff(Hij(1), yi);
Jiy_xi = diff(Hij(2), xi);
Jiy_yi = diff(Hij(2), yi);
Jjx_xi = diff(Hji(1), xi);
Jjx_yi = diff(Hji(1), yi);
Jjy_xi = diff(Hji(2), xi);
Jjy_yi = diff(Hji(2), yi);
Ji = [Jix_xi Jix_yi ; Jiy_xi Jiy_yi]';
Jj = [Jjx_xi Jjx_yi ; Jjy_xi Jjy_yi]';
% The jacobian elements are sometimes complex ONLY THE \partial y ELEMENTS
% They become complex once the relevant sensing regions become tangent to
% their respective cells
% It seems the problem was in the way matlab handles cos(atan2())
% Normal vectors
dHij = diff(Hij, t);
ddHij = diff(dHij, t);
dHji = diff(Hji, t);
ddHji = diff(dHji, t);
ni = ddHij - dot( ddHij, dHij/norm(dHij) ) * dHij/norm(dHij);
nj = ddHji - dot( ddHji, dHji/norm(dHji) ) * dHji/norm(dHji);
% Whether the cell is convex or not depends on the sign of a
ni = - sign(ai) * ni / norm(ni);
nj = - sign(aj) * nj / norm(nj);
% Normal vectors are real so far
% Products
Jni = Ji * ni;
Jnj = Jj * nj;
% Simplify expressions
% Ji = simplify(Ji);
% Jj = simplify(Jj);
% ni = simplify(ni);
% nj = simplify(nj);
% Jni = simplify(Jni);
% Jnj = simplify(Jnj);
% Export matlab functions
FJni = matlabFunction( Jni, 'File','FJni_AWGV');
FJnj = matlabFunction( Jnj, 'File','FJnj_AWGV');
FJi = matlabFunction( Ji, 'File','FJi_AWGV');
FJj = matlabFunction( Jj, 'File','FJj_AWGV');
Fni = matlabFunction( ni, 'File','Fni_AWGV');
Fnj = matlabFunction( nj, 'File','Fnj_AWGV');
elapsed_time = toc;
disp(elapsed_time);
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] S. Papatheodorou, Y. Stergiopoulos, and A. Tzes, Distributed area coverage control with imprecise robot localization, In Proceedings of the 24th Mediterranean Conference on Control and Automation (MED), pp. 214-219, June 21-24, 2016, Athens, Greece
[2] S. Papatheodorou, A. Tzes and K. Giannousakis, Experimental Studies on Distributed Control for Area Coverage using Mobile Robots, In Proceedings of the 25th Mediterranean Conference on Control and Automation (MED), pp. 690-695, July 3-6, 2017, Valletta, Malta
[3] S. Papatheodorou, A. Tzes, K. Giannousakis, and Y. Stergiopoulos, Distributed Area Coverage Control with Imprecise Robot Localization, IEEE Transactions on Automatic Control, ISSN 0018-9286, IEEE [Review pending]
[4] S. Papatheodorou, A. Tzes, and Y. Stergiopoulos, Collaborative Visual Area Coverage, Robotics and Autonomous Systems, ISSN 0921-8890, Volume 92, June 2017, Pages 126–138, Elsevier
[5] S. Papatheodorou and A. Tzes, Cooperative Visual Convex Area Coverage using a Tessellation-free strategy, In Proceedings of the 56th IEEE Conference on Decision and Control (CDC) 2017, December 12-15, 2017, Melbourne, Australia [Accepted]