一、概念定义

在数据处理场景中特征缩放 = 数据规范化，这个两个名词是相同的。

Feature scaling = data normalization

一个数字按照一定规则变小或者变大，这个数字就是特征，变小就是缩，变大就是放。

特征缩放是一种用于规范自变量或数据特征范围的方法。

在数据处理中，这也称为数据规范化，通常在数据预处理步骤中执行。

二、标准化、归一化的原因、用途

2.1 原因

1. 统计建模中，如回归模型，自变量的量纲不一致导致了回归系数无法直接解读或者错误解读；为了消除数据特征之间的量纲影响，我们需要对特征进行归一化处理，使得不同指标之间具有可比性；
2. 机器学习任务和统计学任务中有很多地方要用到“距离”的计算，比如PCA，比如KNN，比如K-means等等，假使算欧式距离，不同维度量纲不同可能会导致距离的计算依赖于量纲较大的那些特征而得到不合理的结果；
3. 参数估计时使用梯度下降，在使用梯度下降的方法求解最优化问题时， 归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。

举例：

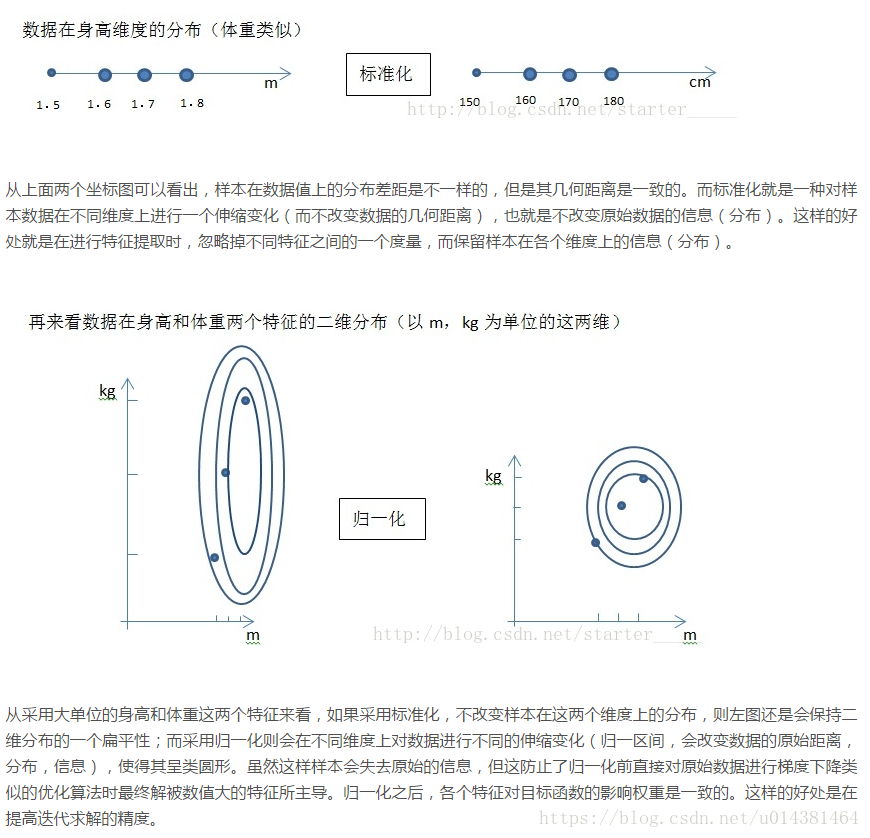
分析一个人的身高和体重对健康的影响，如果使用米（m）和千克（kg）作为单位，那么身高特征会在1.6～1.8m的数值范围内，体重特征会在50～100kg的范围内，分析出来的结果显然会倾向于数值差别比较大的体重特征。

想要得到更为准确的结果，就需要进行特征归一化（Normalization）处理，使各指标处于同一数值量级，以便进行分析。

三、数据归一化的影响

归一化之后等高线变得不再崎岖，$x_1$和$x_2$的更新速度变得更为一致，容易更快地通过梯度下降找到最优解。迭代次数变少，减小梯度下降算法的过程，从而加速模型的生成。

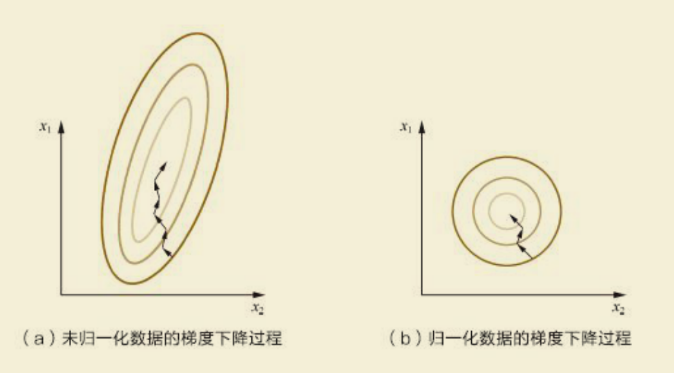
四、常用的3种归一化方法

线性函数归一化（最大最小值归一化）和零均值归一化。

4.1 归一化公式

4.1.1 线性归一化（Min-Max Scaling，即我们一般指的归一化）

它对原始数据进行线性变换，使结果映射到$[0,1]$的范围，实现对原始数据的等比缩放，最通用：
$$X_{norm}=\frac{X-X_{min}}{X_{max}-X_{min}}$$
其中$X_{norm}$为归一化后的数据，$X$为原始数据，$X_{max}$、$X_{min}$分别为原始数据集的最大值和最小值。

注意：对异常值十分灵敏，异常值容易造成偏差！

4.1.2 均值归一化（Mean Normalization）

$$X=\frac{X-\frac{-}{X}}{max(X)-min(X)}$$

4.1.3 零均值归一化（Z-Score Normalization，通常叫标准化）

给予原始数据的均值$\mu$（mean）和标准差$\sigma$（standard deviation）进行数据的标准化。

它会将原始数据映射到均值为0、标准差为1的分布上。
$$z=\frac{x-\mu }{\delta }$$

五、标准化 vs 归一化

六、哪些模型必须归一化

1. 在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，标准化(Z-score standardization)表现更好

2. 在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围

实际应用中，通过梯度下降法求解模型的通常需要归一化，包括线性回归、逻辑回归、支持向量机、神经网络等。

七、哪些模型不需要归一化？

不是所有的模型都需要做归一的，比如模型算法里面有没关于对距离的衡量，没有关于对变量间标准差的衡量。

1. 决策树模型不要要归一化，他采用算法里面没有涉及到任何和距离等有关的，看的是信息增益比，所以在做决策树模型时，通常是不需要将变量做标准化的

2. 概率模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率