一、前言

之前学聚类算法的时候，有层次聚类、系统聚类、K-means聚类、K中心聚类，最后呢，被DBSCAN聚类算法迷上了。

为什么呢，首先它可以发现任何形状的簇，其次我认为它的理论也是比较简单易懂的。接下来的文章里会详细解读一下DBSCAN密度聚类算法。

下面贴上它的官方解释：

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。

该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。

二、DBSCAN聚类算法

DBSCAN是一种基于密度的聚类算法，可以根据样本分布的紧密程度决定，同一类别的样本之间是紧密相连的，不同类别样本联系是比较少的。

DBSCAN算法需要用到参数：

• eps($ϵ$)：一种距离度量，用于定位任何点的邻域内的点
• minPts：聚类在一起的点的最小数目，超过这一阈值才算是一个族群

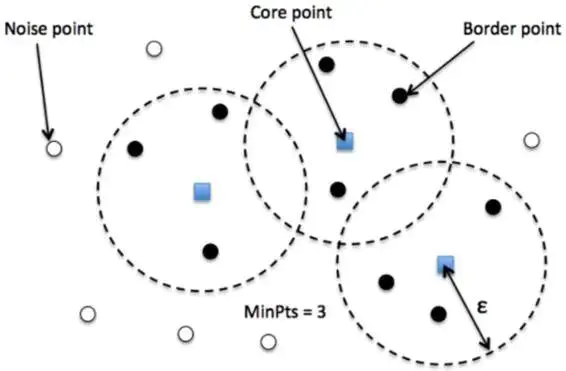
DBSCAN聚类完成后会产生三种类型的点：

• 核心点（Core）——该点表示至少有$m$个点在距离n的范围内
• 边界点（Border） ——该点表示在距离$n$处至少有一个核心
• 噪声点（Noise） ——它既不是核心点也不是边界点。并且它在距离自身$n$的范围内有不到$m$个点

三、DBSCAN算法步骤

1. 算法通过任意选取数据集中的一个点（直到所有的点都访问到）来运行
2. 如果在该点的“ε”半径范围内至少存在“minPoint”点，那么认为所有这些点都属于同一个聚类
3. 通过递归地重复步骤1、步骤2 对每个相邻点的邻域计算来扩展聚类

四、算法的理解

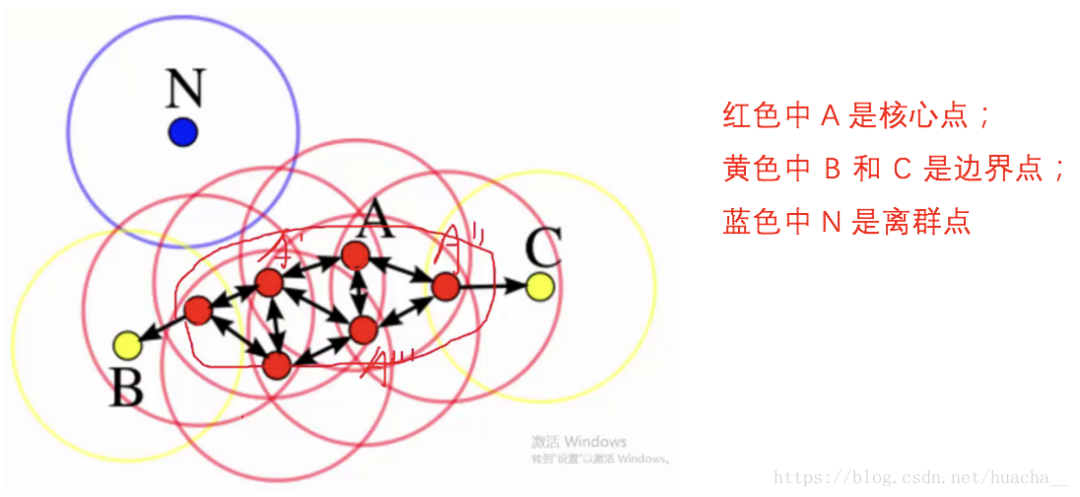
上面这些点是分布在样本空间的众多样本，现在我们的目标是把这些在样本空间中距离相近的聚成一类。

我们发现$A$点附近的点密度较大，红色的圆圈根据一定的规则在这里滚啊滚，最终收纳了$A$附近的5个点，标记为红色也就是定为同一个簇。

其它没有被收纳的根据一样的规则成簇。

形象来说，我们可以认为这是系统在众多样本点中随机选中一个，围绕这个被选中的样本点画一个圆，规定这个圆的半径以及圆内最少包含的样本点，如果在指定半径内有足够多的样本点在内，那么这个圆圈的圆心就转移到这个内部样本点，继续去圈附近其它的样本点，类似传销一样，继续去发展下线。

等到这个滚来滚去的圈发现所圈住的样本点数量少于预先指定的值，就停止了。那么我们称最开始那个点为核心点，如$A$，停下来的那个点为边界点，如$B$、$C$，没得滚的那个点为离群点，如$N$）。

基于密度这点有什么好处呢？

我们知道kmeans聚类算法只能处理球形的簇，也就是一个聚成实心的团（这是因为算法本身计算平均距离的局限）。但往往现实中还会有各种形状，比如下面两张图，环形和不规则形，这个时候，那些传统的聚类算法显然就悲剧了。

于是就思考，样本密度大的成一类呗，这就是DBSCAN聚类算法。

上面提到了红色圆圈滚啊滚的过程，这个过程就包括了DBSCAN算法的两个参数，这两个参数比较难指定，公认的指定方法简单说一下：

• 半径：半径是最难指定的 ，大了，圈住的就多了，簇的个数就少了；反之，簇的个数就多了，这对我们最后的结果是有影响的。我们这个时候K距离可以帮助我们来设定半径r，也就是要找到突变点，比如：
  
  以上虽然是一个可取的方式，但是有时候比较麻烦 ，大部分还是都试一试进行观察，用$k$距离需要做大量实验来观察，很难一次性把这些值都选准。
• MinPts：这个参数就是圈住的点的个数，也相当于是一个密度，一般这个值都是偏小一些，然后进行多次尝试

五、常用评估方法：轮廓系数

这里提一下聚类算法中最常用的评估方法——轮廓系数（Silhouette Coefficient）：

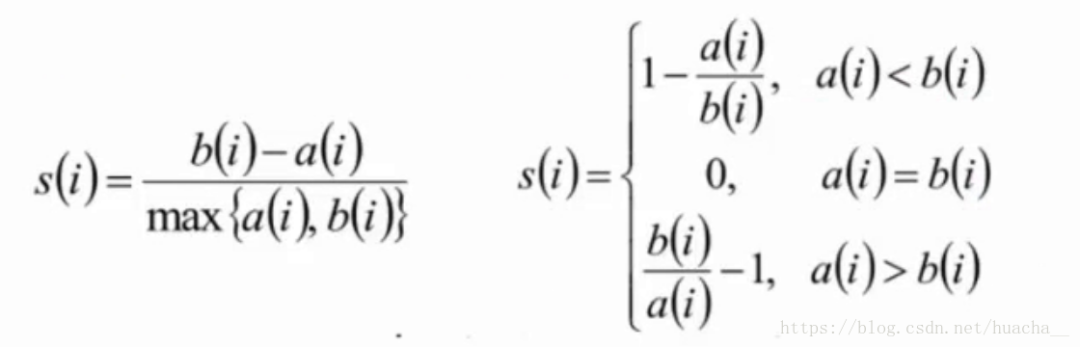
• 计算样本i到同簇其它样本到平均距离$a_i$，$a_i$越小，说明样本i越应该被聚类到该簇（将$a_i$称为样本i到簇内不相似度）；
• 计算样本$i$到其它某簇$C_j$的所有样本的平均距离$b_{ij}$，称为样本$i$与簇$C_j$的不相似度。定义为样本i的簇间不相似度：$b_i=\min (b_{i1},b_{i2},\cdots ,b_{ik2})$；

说明：

• $s_i$接近1，则说明样本i聚类合理；
• $s_i$接近-1，则说明样本i更应该分类到另外的簇；
• 若$s_i$近似为0，则说明样本i在两个簇的边界上。