在实际工作中，我们经常需要分析一组数据的历史走势/趋势情况，比如要从产品数据库中筛选出销量处于上升趋势的产品，或者从股票历史数据库中筛选出一直处于上涨的股票。 那么可以通过分析计算该组数据的差分来模拟求出该组数据走势线的导数，然后通过求导的差分/导数情况判断该组数据的走势情况。从高等数学的导数知识我们知道，如果一个函数的导数大于零，那么该函数在这个区间的趋势处于上升状态，反之，在导数小于0时，函数曲线处于下降状态，而在导数等于0时，函数曲线处于上涨和下降的转折点。通过计算函数有几个零点，可以知道曲线上涨和下降的变化情况，而通过判断导数是大于零还是小于零，我们就能知道曲线是上涨还是下降。

由于产品销售数据或者股价数据都是离散值，而且无法根据这些数据推导出曲线函数，所以直接通过函数求导的方法来判断数据是上涨还是下降是行不通的。但是我们可以求数据的差分并除以步长来近似模拟计算导数。为了演示好看，下面以一组离散正弦数据来进行示例，选正弦函数是因为数据有上下波动趋势，而且正弦函数的导数为余弦函数。

说明：我使用的是Jupyter Notebook环境，方便数据显示

Python里处理数据通常使用Pandas库和Numpy库，计算离散数据的方法就可以使用numpy的方法：

#计算数组a的差分，参数a是一个数组，n是代表几阶差分默认是1，axis是代表按行还是列计算
numpy.diff(a, n=1, axis=-1, prepend=<no value>, append=<no value>)

也可以直接使用Pandas库的方法：

#Pandas库计算差分的方法,periods参数是指定几阶差分，默认是1阶，axis是代表按行还是列计算，默认是按列。按行就改为1
DataFrame.diff(periods=1, axis=0)

先导入相关的库，并设定参数：

#coding utf-8
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #图中文字体设置为黑体

用numpy生成一组模拟正弦离散数值：

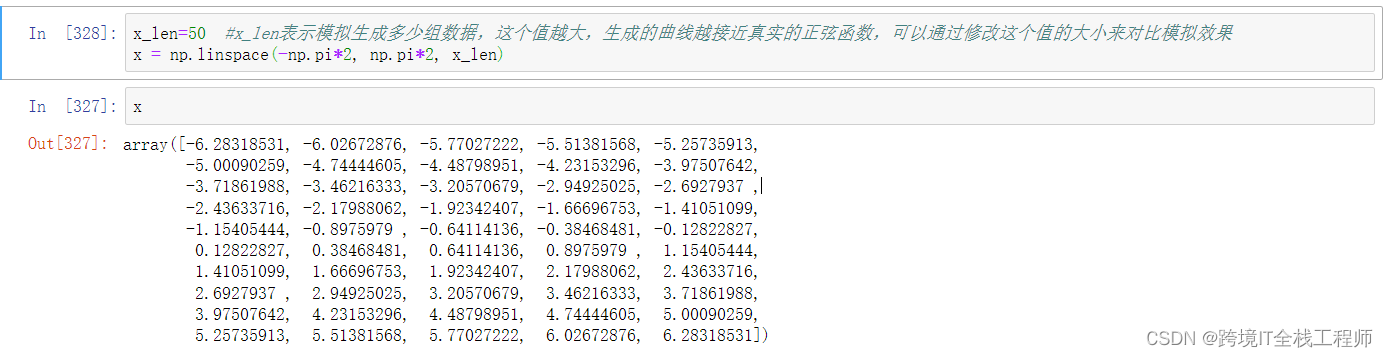
x_len=50  #x_len表示模拟生成多少组数据，这个值越大，生成的曲线越接近真实的正弦函数，可以通过修改这个值的大小来对比模拟效果
x = np.linspace(-np.pi*2, np.pi*2, x_len)

计算数据x的步长：

#导数的公式为dy/dx,当dx接近无线小时，就是函数在x处的导数。因为我们要处理的数据是离散数值，这里仅做一个模拟计算，不要求精确度
#差分取dy=f(x2)-f(x1),即y2-y1， dx=x2-x1,模拟导数=dy/dx, 
#计算dx,也就是x的步长step，这里通过将数组x的最大值减去最小值再除以x数组长度的方法来计算，简单理解就是每个x坐标轴上的间隔
step=(np.max(x)-np.min(x))/len(x)  

使用Pandas生成包含x和y（np.sin(x)）及y的一阶差分数据的数据表：

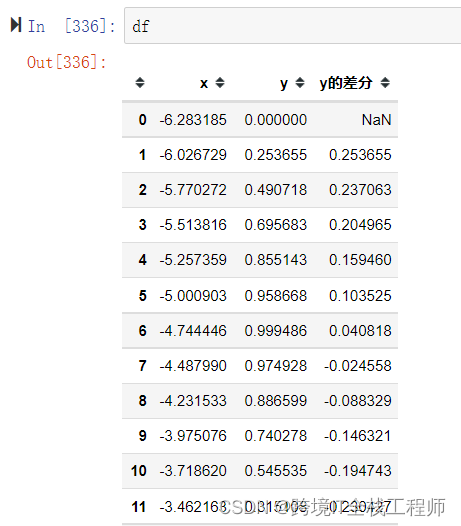
df=pd.DataFrame(data={'x':x,'y':np.sin(x)})  #通过numpy.sin函数计算出x对应的正弦值y，并生成一个pandas数据表
df["y的差分"]=df["y"].diff() #计算y列的差分

使用matplotlib汇总图表：

#汇总对比图
plt.figure(figsize=(20,8))  #设定图画大小
plt.plot(x,df['y'],label='正弦函数sin(x)')
plt.plot(x,df.diff(periods=1)['y'],label="1阶差分dy")  #绘制1阶差分曲线
plt.plot(x,df.diff(periods=1)['y']/step,label="'1阶差分模拟导数y'")  #通过将1阶差分除以步长step得出模拟导数值
plt.plot(x,np.cos(x),label='cos(x)') #用余弦函数做对比
plt.title('离散数据差分和模拟导数',fontsize=16)
plt.xlabel('X')
plt.ylabel('Y')
plt.legend(loc='upper right')
plt.grid()
plt.legend(fontsize=14)

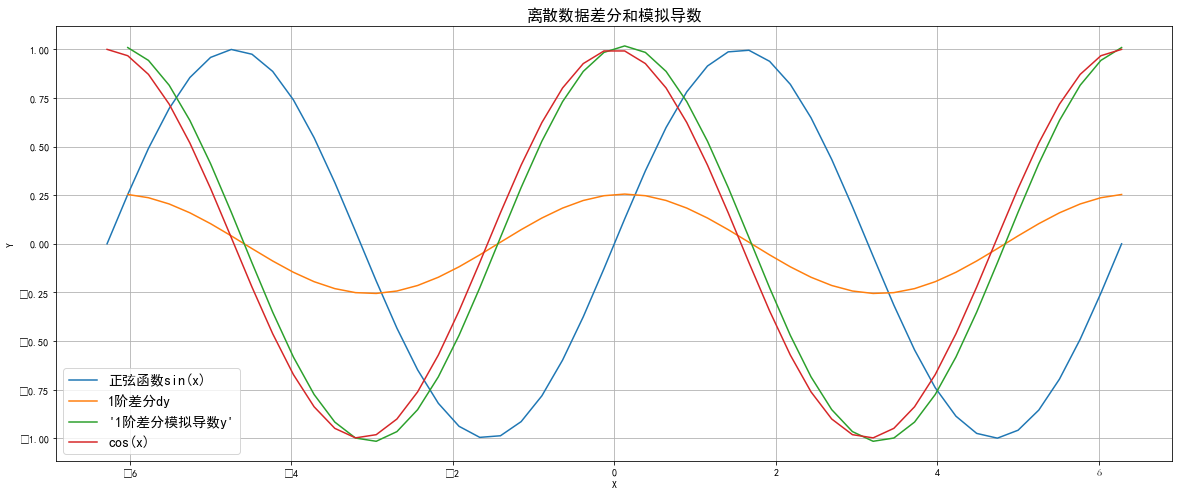
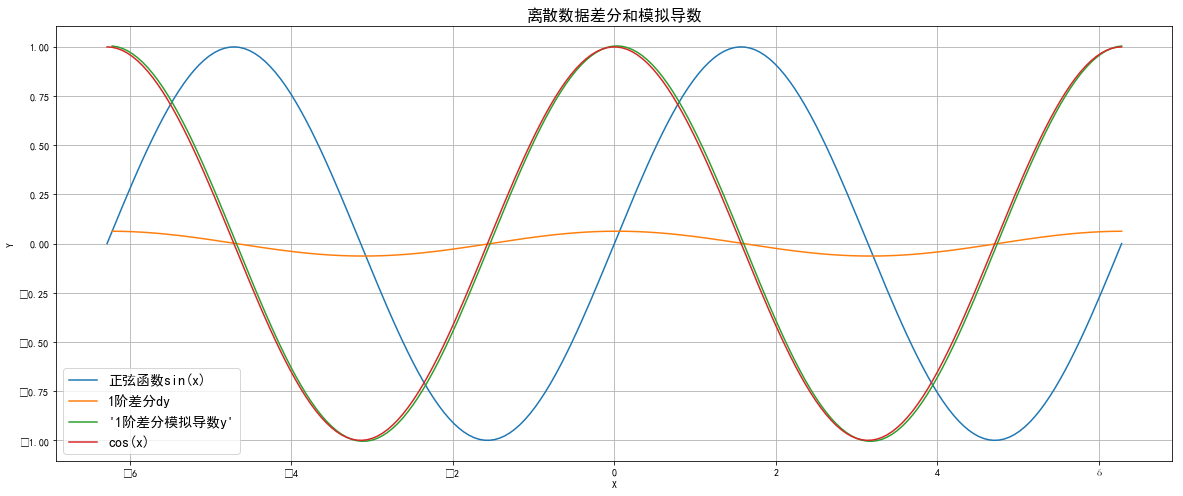
说明：图片有点乱码，左下角坐标轴数字应为负数
图片上：
蓝线是根据x计算的正弦曲线sin(x)
黄线是y的1阶差分，围绕0值上下波动
绿线是根据1阶差分求出来的模拟导数，高等数学里有学过，正弦函数sin(x)的导数为余弦函数cos(x),从图片对比来看，这个模拟导数曲线跟实际的cos(x)函数非常相近，满足实际需要。实际上从我测试的情况来看，当我改变x的数据长度x_len=100时，2条曲线基本上重合在一起。

而如果将步长调大，及把x数据长度调小，2条曲线的偏差就会变大，曲线也变得不光滑：

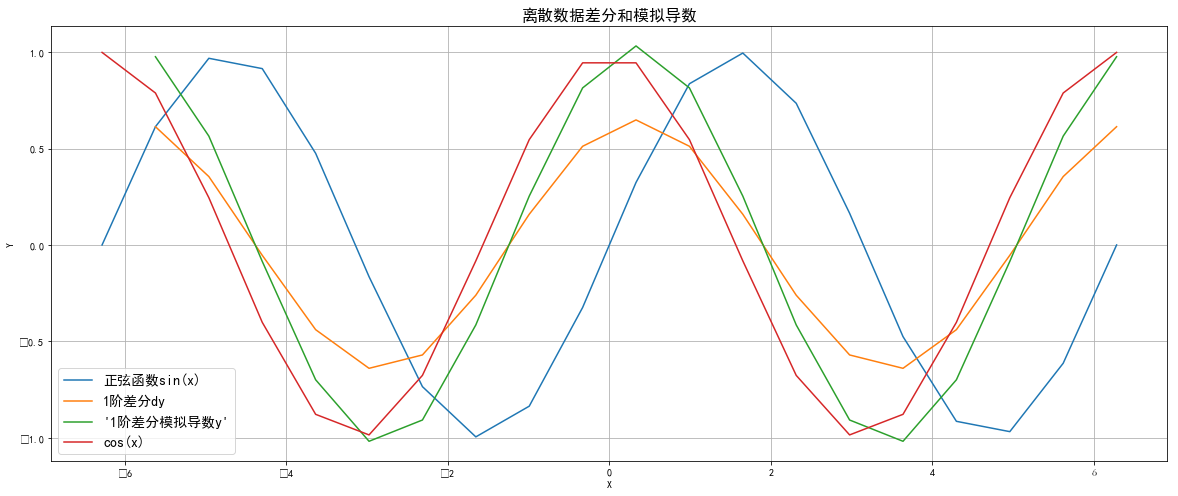
从前面图片我们可以看到，当数据y(通常是我们要分析趋势的数据）处于上升趋势时，它的一阶差分和模拟一阶导数大于0，在y下降趋势时小于0，在拐点时等于0或接近于0，通过pandas 我们可以很容易的计算出有多少这样的差分值和导数值，就可以知道了数据的走势情况。比如说一个股票或产品销售数据一直是处于连续上涨，那么它的一阶差分值和导数值均大于0.

如果进一步分析，我们还可以计算二阶差分和二阶模拟导数，并根据结果的正负情况来判断曲线是加上上涨还是加速下跌。

在分析股票或者产品销售数据的趋势时，我们可能得到的数据长度比较小，模拟偏差比较大，我们可以通过滚动平均等方法来做平滑处理。

不过我们通常的目的只是需要知道数据的趋势，比如上涨或下跌，加速上涨还是加速下跌，并不需要像科学实验一样计算出非常准确的值，所以这种粗略的模拟方法就已经满足我们的实际工作需要了。