目录
前言
初始化
增删
由一个数组构建堆
堆排序
TOPK问题
前言
我们都知道二叉树是度为 2 的树,如果在一个完全二叉树里,所有的子结点都小于他的父结点,那么它就是堆。这样的堆被称之为大堆,反之则称为小堆。
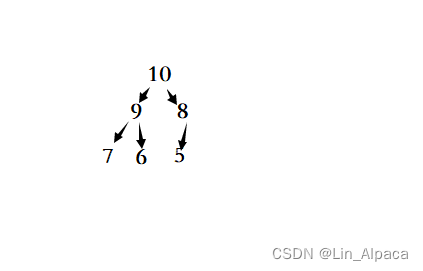
虽然我们画出它的模型是完全二叉树的样子,但实际上堆的数据是存放在一个一维数组里的,不用惊慌,如下三个公式便可以解决我们于堆访问的问题。归根结底还是数学问题。

初始化
前面讲过,堆的数据的存放在数组里面的,因此构建的是一个顺序表的结构。并给予初始数值,因为将开辟空间一并放到 checkcapacity 里,所以这里就只是赋值成0而已。
typedef int heaptype;
typedef struct heap
{
heaptype* a;
int size;
int capacity;
}heap;//堆的初始化
void Heapinit(heap* hp)
{
hp->a = NULL;
hp->size = hp->capacity = 0;
}销毁
堆的销毁十分简单,直接把申请的空间全部释放就可以了。
// 堆的销毁
void HeapDestory(heap* hp)
{
assert(hp);
assert(hp->a);
free(hp->a);
hp->a = NULL; //回归初始状态
hp->size = hp->capacity = 0;
}增删
插入数据
作为一个数组,插入数据最佳的地方应该是数组的尾部。插入前还得检查一下数组的大小是否够用,否则扩容数组。
void checkcapacity(heap* hp)
{
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2; //初始化为4,否则大小翻倍
heaptype* narr = (heaptype*)realloc(hp->a, sizeof(heaptype) * newcapacity);
if (narr == NULL)
{
perror(realloc);
exit(-1);
}
hp->a = narr; //更新数据
hp->capacity = newcapacity;
}
}但仅仅插入是不行的,为了保证堆依然成立,我们还需要对数据的位置进行调整。(这里构建的是小堆)
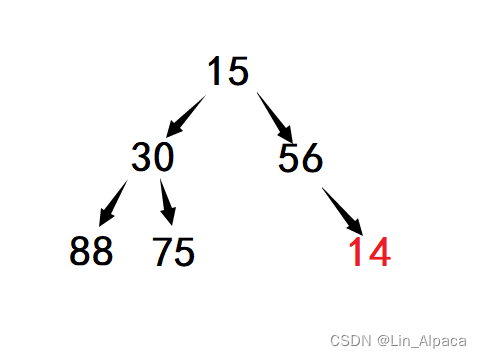
我们应该注意到的是,小堆的定义是每一个子结点都要大于它的父结点,这里我们只需要让新插入的这个数据逐步地于它的父节点比较,小于则交换,大于就不再进行移动。
void adjustup(heap* hp)
{
int child = hp->size; //找到子结点的下标
int parent = (child-1)/2; //找到与该子结点对应的父结点
while (child > 0) //堆顶的下标为0位于堆顶无需再调整
{
if (hp->a[child] < hp->a[parent]) //子结点小于父结点则交换
{
swap(&hp->a[child], &hp->a[parent]);
child = parent;
parent = (child - 1) / 2; //找当前位置的父结点
}
else
{
break; //大于则无需调整
}
}
} 
把这些统合起来就完成了往堆里插入一个新值。
// 堆的插入(小堆)
void HeapPush(heap* hp, heaptype x)
{
assert(hp);
checkcapacity(hp);
hp->a[hp->size] = x;
adjustup(hp);
hp->size++;
}删除堆顶数据
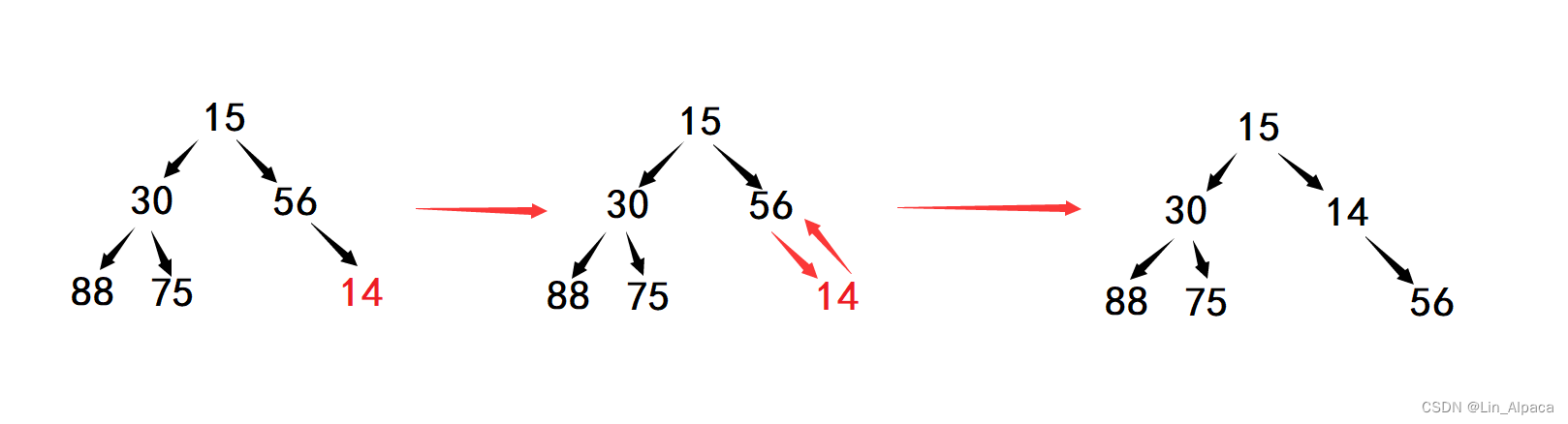
仔细思考,我们会发现若直接删除堆顶是十分困难的,这时候我们不禁想:若堆顶的那个数据也在数组的尾部就好了。这无疑是为这个步骤提供了一个绝佳的思路!!!我们可以把堆顶与堆底的数值交换,把最后面的值删除之后,对堆顶的数据进行向下调整,由于原本堆底的值就是最大的值,因此调整结束后其仍会回归堆底。
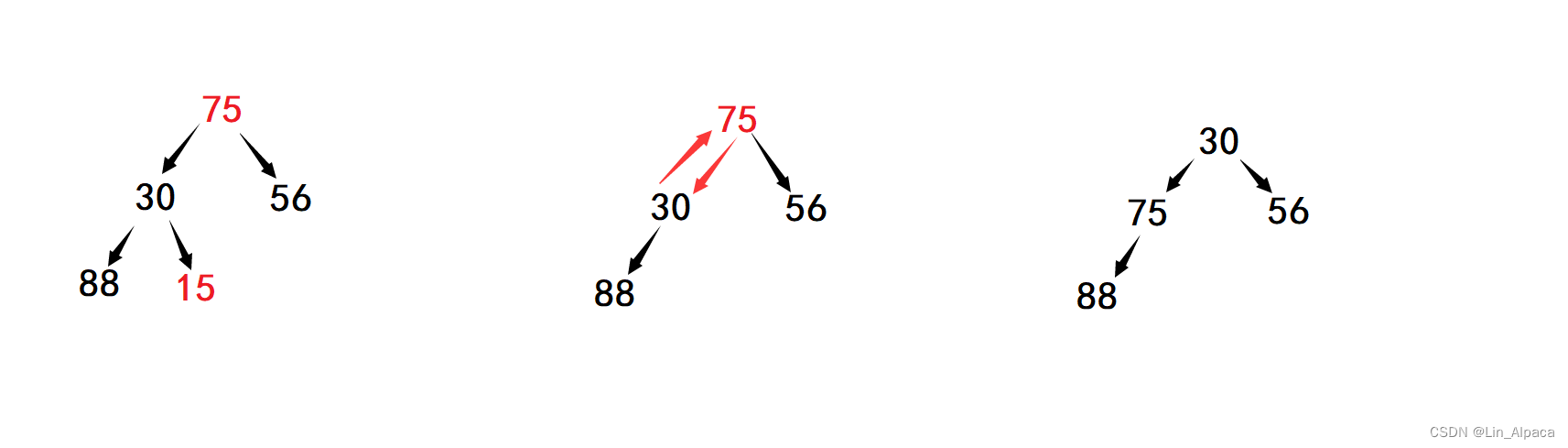
void adjustdown(heaptype* a, int n, int root) //n是数组的大小
{
int parent = root; //找到向下调整的初始值
int child = parent * 2 + 1; //往下找其左孩子
while (parent < n)
{
if (child + 1 < n && a[child] > a[child + 1]) //找孩子里最小的那个
{
child++;
}
if (child < n && a[parent] > a[child]) //父结点大于子结点就交换
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1; //找该结点对应的子结点
}
else
{
break; //小于则停止调整
}
}
}删除数组最后一个只需要调整size的值,并不需要对其进行其他调整。
// 堆顶的删除
void HeapPop(heap* hp)
{
assert(hp);
assert(hp->a);
swap(&hp->a[hp->size - 1], &hp->a[0]);
hp->size--;
adjustdown(hp->a, hp->size, 0);
}堆顶数据 数据个数 判空
对基本数值判定就可以完成。
// 取堆顶的数据
heaptype HeapTop(heap* hp)
{
assert(hp);
assert(hp->a);
return hp->a[0];
}
// 堆的数据个数
int HeapSize(heap* hp)
{
assert(hp);
return hp->size;
}
// 堆的判空
bool HeapEmpty(heap* hp)
{
assert(hp);
if (hp->size)
{
return true;
}
return false;
}
由一个数组构建堆
需要清楚的一件事是,我们能够使用向下调整的前提是下面两个堆都是小堆,因此若要由一个数组构建堆并不只是一个劲地向下调整就可以解决的。

仔细一想,若我们从尾部向下调整上去,似乎结果就有所不同,我们只需要找到数组最后一个数的父结点,这时候向下调整就只会在这(2~3)个数直接寻找最小值放在该父结点上。之后找到最靠近这个父结点的另一父结点再次进行调整,直到到达堆顶完成堆的构建。
void HeapCreate(heap* hp, heaptype* a, int n)
{
heaptype* narr = (heaptype*)malloc(sizeof(heaptype)*n); //开辟堆的空间
if (narr == NULL)
{
perror(malloc);
exit(-1);
}
hp->a = narr;
hp->size = 0;
hp->capacity = n;
for (int i = 0; i < n; i++) //导入原数组
{
checkcapacity(hp);
hp->a[i] = a[i];
hp->size++;
}
for (int i = (n - 1 - 1) / 2; i >= 0; i--) //从下往上逐步构建小堆
{
adjustdown(hp, hp->size, i);
}
}堆排序
我们都知道,在小堆内堆顶的数据就是整个堆最小的,因此可以利用这个思想进行对数组的排序。把最小的数放在数组最后,其他的数继续排序,直到全部完成。因此构建大堆便排升序,构建小堆则排降序。这样子使得排序的实践复杂度大大减小,达到提高运行效率的结果。
void HeapSort(heaptype* a, int n)
{
assert(a);
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
adjustdown(a, n, i); //构建小堆排降序
}
int end = n-1; //找到数组尾端
while (end)
{
swap(&a[0], &a[end]); //最小值与最尾值交换
adjustdown(a, end, 0); //向下调整
end--; //把已调整完的值剔除于排序内
}
}TOPK问题
要求出最大的几个数,主要的思想便是先用前 k 个值创建一个小堆,若有值大于这个堆里最小的数(堆顶)则插入到堆里而剔除原堆顶的元素。遍历完整个数组后,堆里剩下的就是最大的 k 个数了。
void HeapSort(heaptype* a, int n)
{
assert(a);
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
adjustdown(a, n, i); //构建小堆排降序
}
int end = n-1; //找到数组尾端
while (end)
{
swap(&a[0], &a[end]); //最小值与最尾值交换
adjustdown(a, end, 0); //向下调整
end--; //把已调整完的值剔除于排序内
}
}
void PrintTopK(int* a, int n, int k)
{
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror(malloc);
exit(-1);
}
for (int i = 0; i < k; i++) //先取前k个数放到这个堆里面
{
minheap[i] = a[i];
}
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
adjustdown(minheap, k, i); //调整成一个小堆
}
for (int i = k; i < n; i++)
{
if (a[i] > minheap[0])
{
swap(&a[i], &minheap[0]); //大于堆顶就交换插进来
adjustdown(minheap, k, 0); //向下调整找到定位
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
}这样今天的堆与堆排序的讲解就到这里结束了,如果有帮助到你还希望能给我一键三连,我们下次再见。