【问题描述】给定n个矩阵$M_1,M_2...M_n$，他们的维数分别是$r_1\ast c_1,r_2\ast c_2...r_n\ast c_n$，要求使用【动态规划】的策略求解矩阵连乘的最优计算代价(总乘法次数最少)。题目保证矩阵相乘一定是有效的。

例如有三个矩阵$M_1，M_2，M_3$，他们的维度分别是$2\ast 10,10\ast 2，2\ast 10$。按照矩阵乘法的结合律，可以先把$M_1$和$M_2$相乘，然后把结果和$M_3$相乘，总的乘法次数为$2\ast 10\ast 2+2\ast 2\ast 10=80$次；也可以先把$M_2$和$M_3$相乘，再用$M_1$去相乘，这种方式下总的乘法次数为$10\ast 2\ast 10+2\ast 10\ast 10=400$次。因此最优计算代价为80。
【输入形式】输入的第1行中有1个数字$n$，表示矩阵的个数；接下来$n$行，每行2个整数$r_i$和$c_i$，分别表示矩阵$M_i$的行数和列数。
【输出形式】输出1行中有一个数字，表示$n$个矩阵相乘的最优计算代价。
【样例输入】

3

2 10

10 2

2 10
【样例输出】

80
【说明】

$n>=2$

$1<=r_i,c_i<=20$

题解：

我们定义$dp[i][j]$为从第$i$个矩阵连乘到第$j$个矩阵的最优代价，那么我们可以得到状态转移方程：

$\forall k\in [i,j),dp[i][j]=dp[i][k]+dp[k+1][j]+r[i]\ast c[k]\ast c[j]$

解释一下，这个方程的意思就是从第$i$号矩阵到第$j$号矩阵的连乘的最优代价等于第$i$个矩阵到第$k$个矩阵的最优代价加上第$k+1$到第$j$个矩阵的最优代价再加上这两边矩阵相乘的代价，其中$k$是大于等于$i$且小于$j$的一个正整数。

更通俗地来说，第$k$个矩阵作为第$i$号矩阵到第$j$号矩阵的一个分割线，把整条矩阵链分成了两部分，那么总的最优代价就等于左边部分的最优代价加上右边部分的最优代价，再加上把左右两部分拼回去的代价。

相当于说，我分割好后，先把左边的矩阵链按照最优的方法计算完得到一个矩阵A，并把代价记下来，再把右边的矩阵链也按照最优的方法计算完得到另一个矩阵B，也把代价记下来，最终，将A与B相乘，这也会产生代价，最后把这三个代价相加，就得到整条矩阵链计算的代价。

但是，不同的$k$会得到不同的代价，因此要在k的取值范围内枚举并计算将每一个$k$作为分割线时，所产生的代价是多少，并取最小值作为整条矩阵链的最优代价。

说了这么多，可能还需要补充一下矩阵相乘的代价需要怎样计算，举例来说，一个$1\times 3$的矩阵和一个$3\times 5$的矩阵相乘所产生的计算代价就是$1\times 3\times 5$；一个$1\times 5$的矩阵和一个$5\times 5$的矩阵相乘所产生的计算代价就是$1\times 5\times 5$。

根据以上举例，可以总结出规律：

一个$n_1\times m_1$的矩阵和一个$n_2\times m_2$的矩阵相乘所产生的计算代价就是$n_1\times m_1\times m_2$，当然，众所周知，两个矩阵相乘的必要条件是$m_1=n_2$，所以把$m_1$替换成$n_2$也是ok的。

其实这个代价仅代表的是两个矩阵相乘所需要使用乘法的次数，我们知道，矩阵相乘不仅需要乘法，也需要加法，但如果单单只是想要比较计算代价来得出最优方法，省略掉加法代价也无伤大雅。

另外，对于一个矩阵链$M_1\times M_2\times M_3\times ...\times M_n$来说，它的答案矩阵的规模一定是$r_1\times c_n$

明确了状态转移方程的意义之后，便需要知道初始状态的情形

• 由于矩阵本身不需要计算，因此所有的$dp[i][i]$都等于0
• 考虑矩阵链中只包含两个矩阵的情形，那么$dp[1][2]=dp[1][1]+dp[2][2]+r[1]\ast r[1]\ast c[2]$
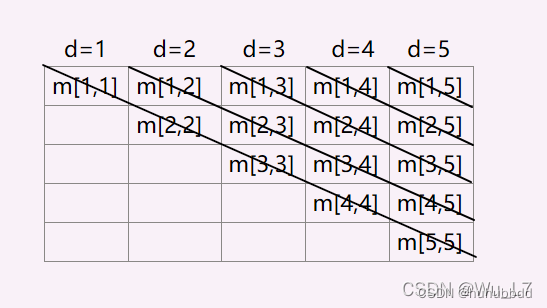
• 如果我们画出$dp$表可以看到$dp[1][1]$和$dp[2][2]$是位于$dp[1][2]$的左下角的，甚至来说，对于任意一个$dp[i][j]$来说，它的求解都需要用到它左下方的值，如果按照一般的$dp$路线，从第一行开始，每一行从第一个开始向右枚举，那么$dp[i][j]$左下方的值根本就没有求解过，何谈根据最优子结构递推得出最优解？

因此，我们dp的路线也有所改变，具体做法代码中已给出，外层循环枚举每一条对角线$d$，第二层循环枚举行号$i$，根据行号$i$和对角线号$d$可以得出列号$t=i+d-1$，最后一层循环枚举$k$。

代码：

#include <iostream>
using namespace std;
const int inf = 0x3f3f3f3f;
int n, r[21], c[21], dp[21][21];
//def:dp[i][j]代表从第i个矩阵到第j个矩阵的连乘的最优代价

void init() {
    for (int i = 1; i <= n; i++) {
        dp[i][i] = 0;
    }
}

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> r[i] >> c[i];
    }
    init();
    for (int d = 2; d <= n; d++) {
        for (int i = 1; i <= n - d + 1; i++) {
            int t = i + d - 1; dp[i][t] = inf;
            for (int k = i; k < t; k++) {
                int cost = dp[i][k] + dp[k + 1][t] + r[i] * c[k] * c[t];
                if (cost < dp[i][t]) {
                    dp[i][t] = cost;
                }
            }
        }
    }
    cout << dp[1][n];
}