目录
实现矩阵连乘积
题目
问题分析
算法分析
时间复杂度
代码实现
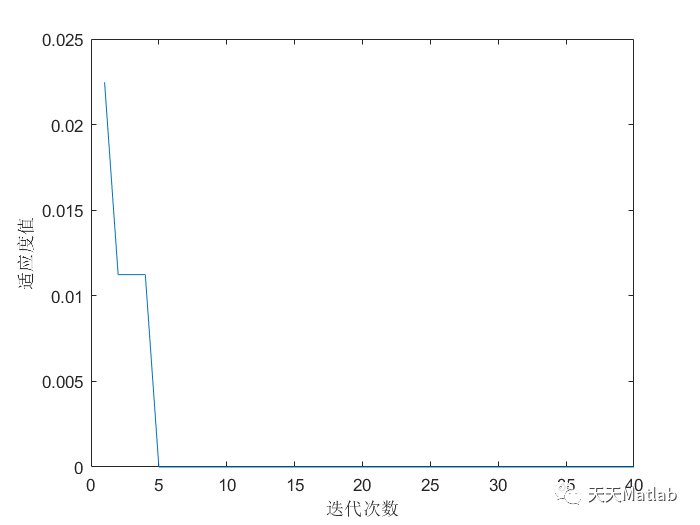
执行结果
动态规划
基本思想
举例
个人主页:天寒雨落的博客_CSDN博客-初学者入门C语言,python,数据库领域博主
💬 热门专栏:初学者入门C语言_天寒雨落的博客-CSDN博客
每日赠语:没有窘迫的失败,就不会有自豪的成功;失败不可怕,只要能从失败中站起来。
实现矩阵连乘积
题目
给定n个矩阵{A1,A2,…,An},其中A(i)与A(i+1)是可乘的,i=1,2…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
问题分析
算法分析
RecurMatrixChain:A1,A2,…,An可乘。
令A1:p0xp1
A2:p1xp2
A3:p2xp3
......
An:An-1xAn
注:以上数字均为下标
当n=2,A1A2:p0xp1xp2
当n=3,A1A2A3,此时根据矩阵乘法的结合律可分两种情况,去最优解即取要的数乘次数最少的:
- A1(A2A3):p1xp2xp3+p0xp1xp3(其中p1xp2xp3是A2A3的数乘次数,p0xp1xp3是p1和A2A3乘积结果后新的矩阵的数乘次数)
- (A1A2)A3:p0xp1xp2+p0xp2xp3(其中p0xp1xp2是A1A2的数乘次数,p0xp1xp3是p3和A1A2乘积结果后新的矩阵的数乘次数)
令f(n)为求解矩阵连乘积需要的最少数乘次数
f(n)=min{f(k)+f(n-k)+p0xpkxpn}
f(k)+f(n-k)是拆分,p0xpkxpn是合并
i<=k<j,假设在第k位置上找到最优解,则问题变成了两个子问题(Ai...Ak)(Ak+1...Aj)
用m[i][j]表示矩阵连乘的最优值,则初始状态为m[i,j](i=j),最终状态为m[1,n](i=1,j=n)
:
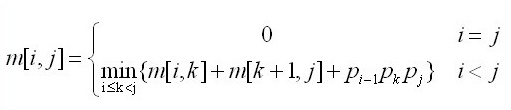
用s[i][j]记录断开位置
时间复杂度
p(n)=O(n^3)
代码实现
//重叠子问题的递归最优解
//A1 30*35 A2 35*15 A3 15*5 A4 5*10 A5 10*20 A6 20*25
//p[0-6]={30,35,15,5,10,20,25}
#include <iostream>
using namespace std;
int RecurMatrixChain(int i, int j, int **s, int *p); //递归求最优解
void Traceback(int i, int j, int **s); //构造最优解
int main() {
int L = 7;
int p[L] = {30, 35, 15, 5, 10, 20, 25};
int **s = new int *[L];
for (int i = 0; i < L; i++) {
s[i] = new int[L];
}
cout << "矩阵的最少计算次数为:" << RecurMatrixChain(1, 6, s, p) << endl;
cout << "矩阵最优计算次序为:" << endl;
Traceback(1, 6, s);
return 0;
}
int RecurMatrixChain(int i, int j, int **s, int *p) {
if (i == j)
return 0;
int u = RecurMatrixChain(i, i, s, p) + RecurMatrixChain(i + 1, j, s, p) + p[i - 1] * p[i] * p[j];
s[i][j] = i;
for (int k = i + 1; k < j; k++) {
int t = RecurMatrixChain(i, k, s, p) + RecurMatrixChain(k + 1, j, s, p) + p[i - 1] * p[k] * p[j];
if (t < u) {
u = t;
s[i][j] = k;
}
}
return u;
}
void Traceback(int i, int j, int **s) {
if (i == j)
return;
Traceback(i, s[i][j], s);
Traceback(s[i][j] + 1, j, s);
printf("Multiply (A%d and A%d),断开位置是:%d\n", i, j, s[i][j]);
}
执行结果
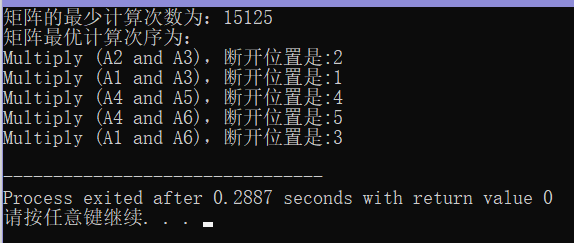
动态规划
基本思想
其基本思想是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解,经分解得到子问题往往不是互相独立的
举例
你知道两个1相加等于2,问你三个1相加你是拿前面的两个1相加的结果加上1呢,还是再用1+1+1,你肯定会用前面的那种方法对吧,这就是动态规划,(1+1)就是(1+1+1)的子问题,且并不是相互独立,你得到了(1+1)就好得到(1+1+1)了
👍+✏️+⭐️是对博主最大的鼓励与支持!!!