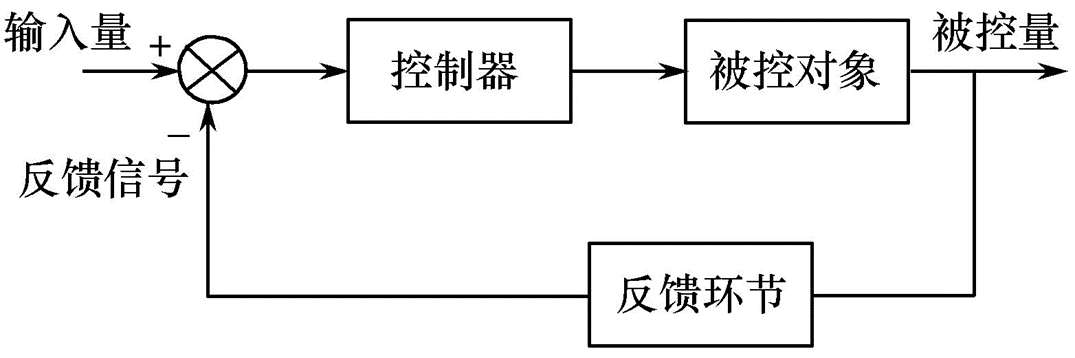
逻辑回归
一、假设函数
h
θ
(
x
)
=
g
(
θ
T
X
)
=
1
1
+
e
−
θ
T
X
(
S
i
g
m
o
i
d
函
数
)
h_\theta(x) = g(\theta^TX)=\frac{1}{1+e^{-\theta^TX}} \qquad \qquad \qquad (Sigmoid函数)
hθ(x)=g(θTX)=1+e−θTX1(Sigmoid函数)

X取值范围是
(
−
∞
,
+
∞
)
(-\infty, +\infty)
(−∞,+∞)
Y的取值范围是(0, 1)
{
θ
T
X
小
于
0
=
⇒
h
θ
(
x
)
<
0.5
=
⇒
y
=
0
θ
T
X
>
0
=
⇒
h
θ
(
x
)
>
0.5
=
⇒
y
=
1
θ
T
X
=
0
=
⇒
h
θ
(
x
)
=
0.5
=
⇒
决
策
边
界
\begin{cases} & \theta^TX小于0 =\Rightarrow h_\theta(x) < 0.5 =\Rightarrow y=0 \\ & \theta^TX>0 =\Rightarrow h_\theta(x) > 0.5 =\Rightarrow y=1\\ & \theta^TX=0 =\Rightarrow h_\theta(x) = 0.5 =\Rightarrow 决策边界 \end{cases}
⎩⎪⎨⎪⎧θTX小于0=⇒hθ(x)<0.5=⇒y=0θTX>0=⇒hθ(x)>0.5=⇒y=1θTX=0=⇒hθ(x)=0.5=⇒决策边界
二、代价函数 - 最大似然估计
线性回归的代价函数是平方损失函数,将逻辑回归的假设函数代入公式后的损失函数是一个非凸函数,有很多个局部最优解,没有办法快速的获得全局最优解,于是我们就用上了最大似然估计:
J
(
θ
)
=
{
if y=1 then
−
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
if y=0 then
−
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
J(\theta)=\begin{cases} & \text{ if y=1 then } -y^{(i)}log(h_\theta(x^{(i)}) \\ & \text{ if y=0 then } -(1-y^{(i)})log(1-h_\theta(x^{(i)})) \end{cases}
J(θ)={ if y=1 then −y(i)log(hθ(x(i)) if y=0 then −(1−y(i))log(1−hθ(x(i)))
整合后
J
(
θ
)
=
1
m
(
−
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
−
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
)
J(\theta)=\frac{1}{m}(-y^{(i)}log(h_\theta(x^{(i)})) - (1-y^{(i)})log(1-h_\theta(x^{(i)})))
J(θ)=m1(−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i))))
三、目标函数
M i n J ( θ ) MinJ(\theta) MinJ(θ)
四、求解目标函数
1、梯度下降
2、正规方程
五、为什么是Sigmoid函数
- 输入范围是−∞→+∞,输出为0,1,正好满足概率分布为(0,1)的要求
- 单调上升的可导函数
@ 学必求其心得,业必贵其专精