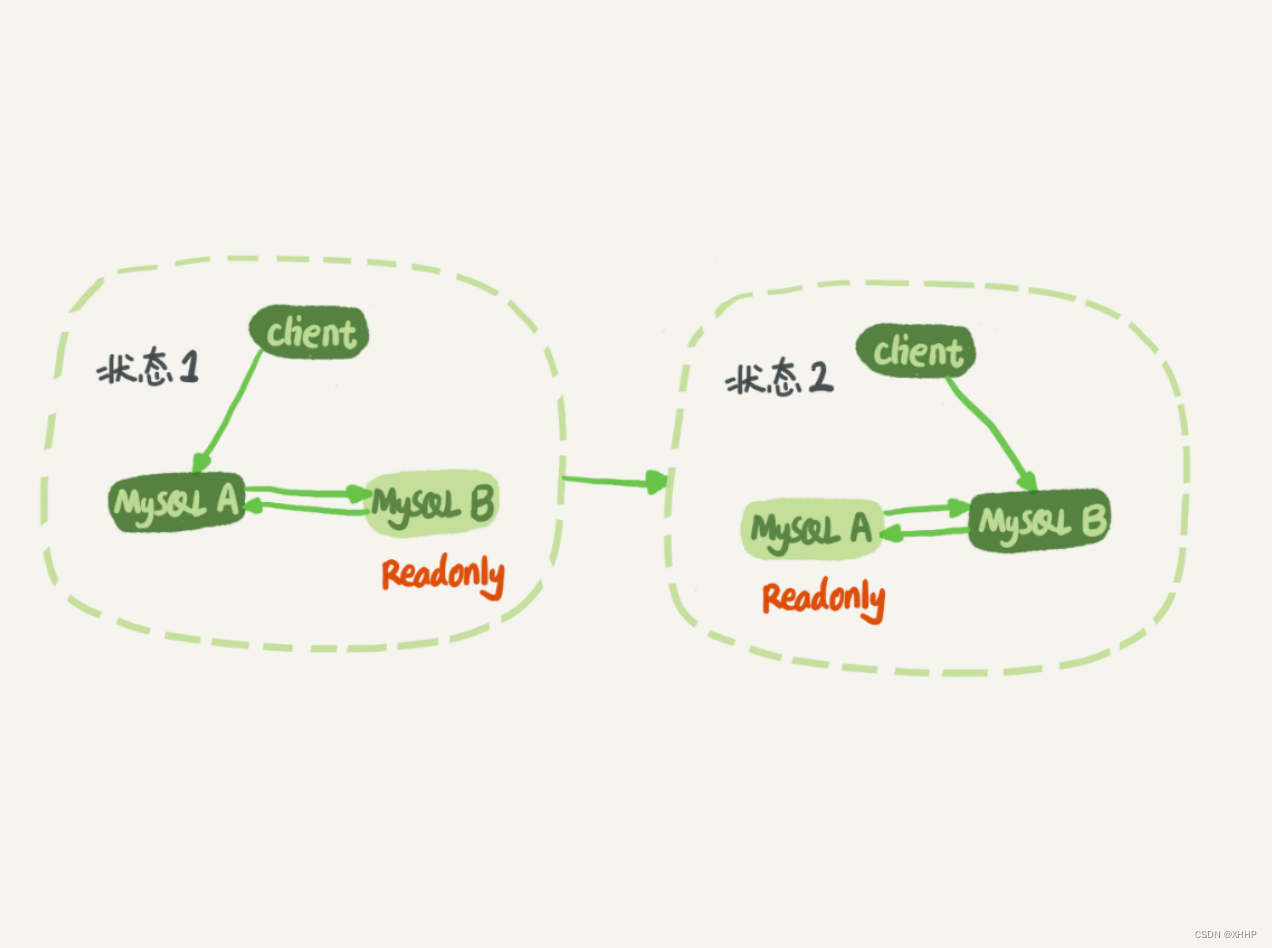
1、复正弦信号和线性时不变系统的频率相应
| 卷积积分和卷积和 | 傅里叶变换 |
|---|---|
| 冲激表示信号 | 正弦表示信号 |
| 输入信号表示为延迟冲激的加权叠加 | 输入信号为复正弦信号的加权叠加 |
| 输出可以用卷积的形式来表示 | 输出可以用傅里叶的形式来表示 |
(1)频率响应Frequency response
线性时不变系统对正弦输入的相应引出了一个系统的特征量
The response of an LTI system to a sinusoidal input(正弦输入) lead to a characterization of system behavior that is termed the frequency response of the LTI system.
(2)离散LTI系统的频率响应Frequency response of Discrete-time LTI system

1)Impulse response of discrete-time LTI system = h[n], input = x[n] =exp(jΩn)
2)Output
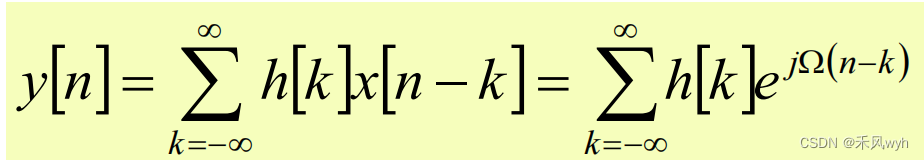
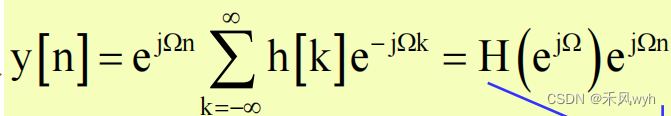
3)Frequency Response

(3)连续LTI系统的频率响应Frequency response of Continuous-time LTI system
1) Impulse response of continuous-time LTI system = h(t), input = x(t) = exp(jwt)
2)Output
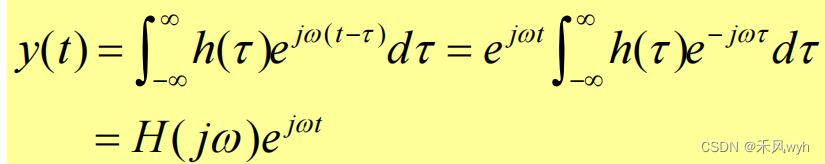
3)Frequency Response


(4)特征量和特征函数-连续时间(Eigenvalue and eigenfunction of LTI system-Continuous-time)
1) Eigenrepresentation
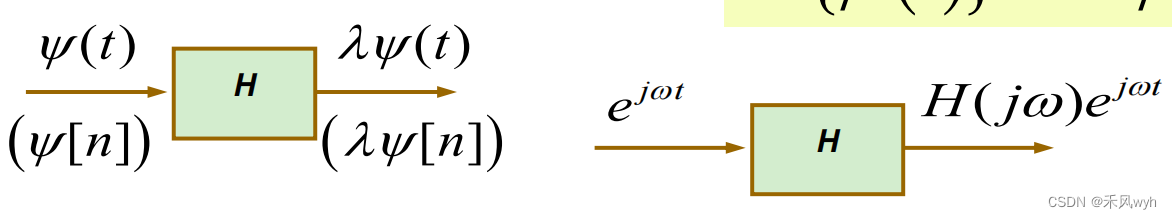
2)Eigenfunction
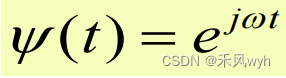
3)Eigenvalue
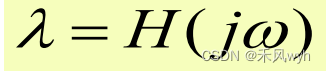
Arbitrary input = weighted superpositions of eigenfunctions

(5)特征量和特征函数-l离散时间(Eigenvalue and eigenfunction of LTI system-Discrete-time)
1) Eigenrepresentation
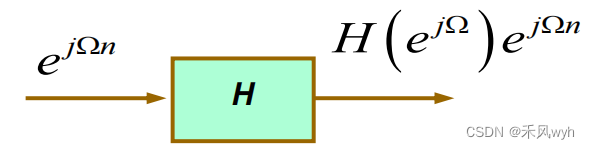
2)Eigenfunction
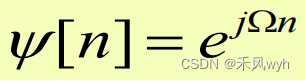
3)Eigenvalue
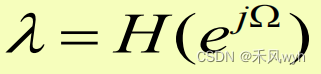

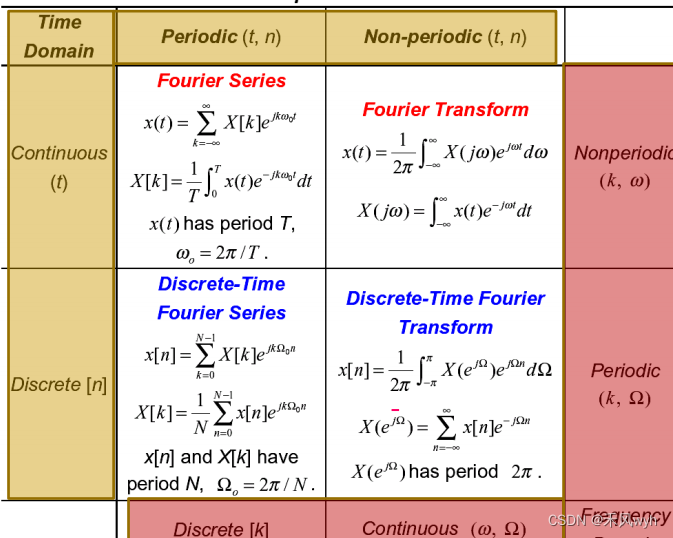
2、4种信号的傅里叶表示Fourier Representations for Four classes of Signals

(1)周期信号Periodic Signals: Fourier Series Representations
1) Discrete-time signal with fundamental period N

2) Continuous-time signal with fundamental period T


3) The complex sinusoids exp(jkΩn) are N-periodics in the frequency index k

4)Continuous-time complex sinusoid exp(jkwt) with distinct frequencies kw are always distinct
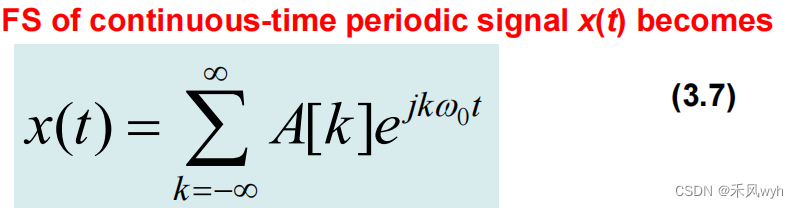
5) Mean-square error (MSE) between the signal and its series representation
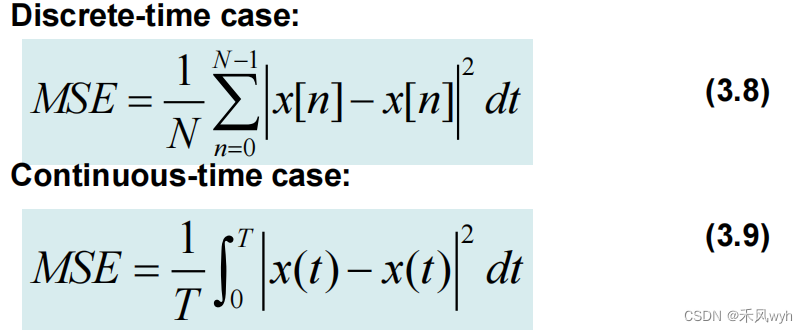
(2)非周期信号
1) FT of continuous-time signal
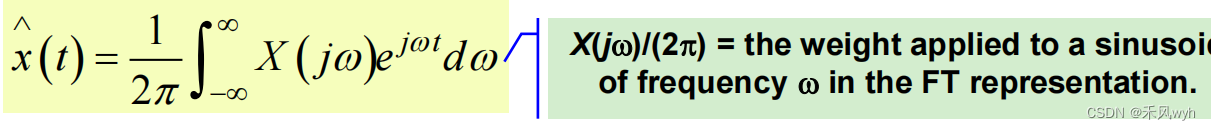
2) DTFT of discrete-time signal
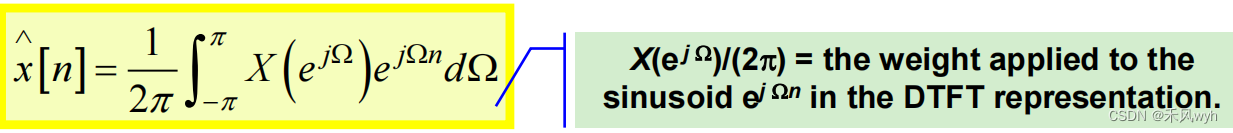
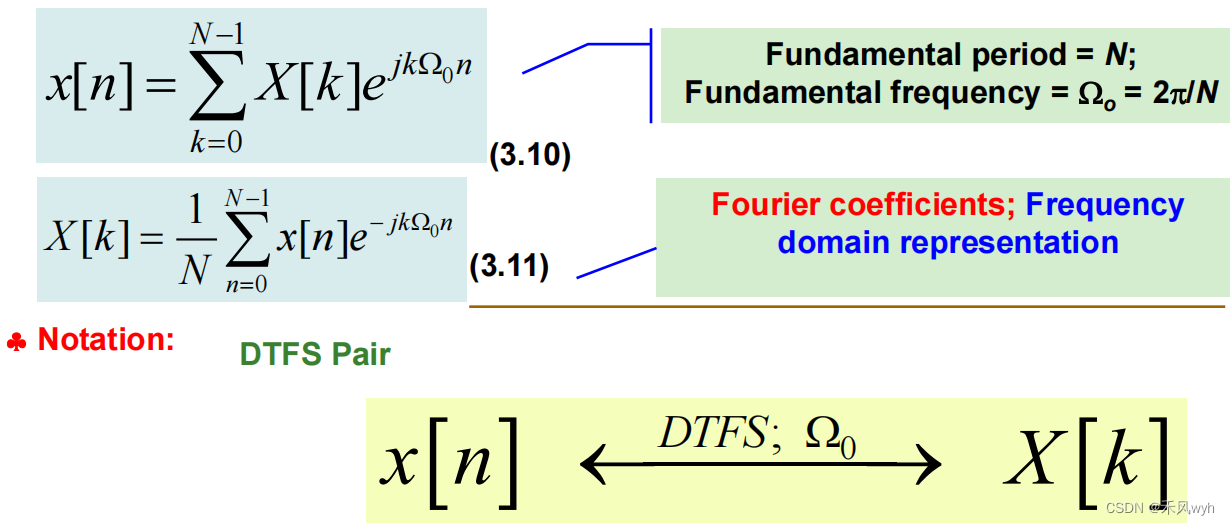
(3)离散时间周期信号:离散时间傅里叶级数
1) DTFS pair of periodic signal x[n]
2) Determining DTFS Coefficients
①单个正弦信号
②多个正弦信号的叠加

③基于冲激序列的信号


④根据图像求解Calculation by Inspection

⑤方波

3) Determining DTFS Inverse Transformation
①单个正弦信号

②多个正弦信号的叠加
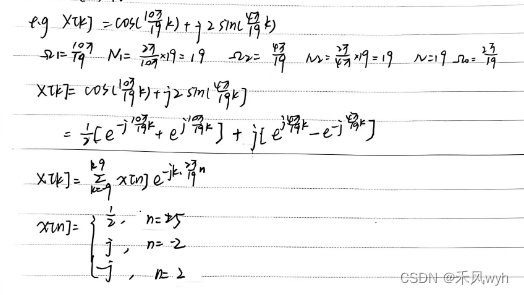
③基于冲激序列的信号

④根据图像求解
(4)连续时间周期信号:傅里叶级数
1) Fourier series pair ⎯ Exponential FS
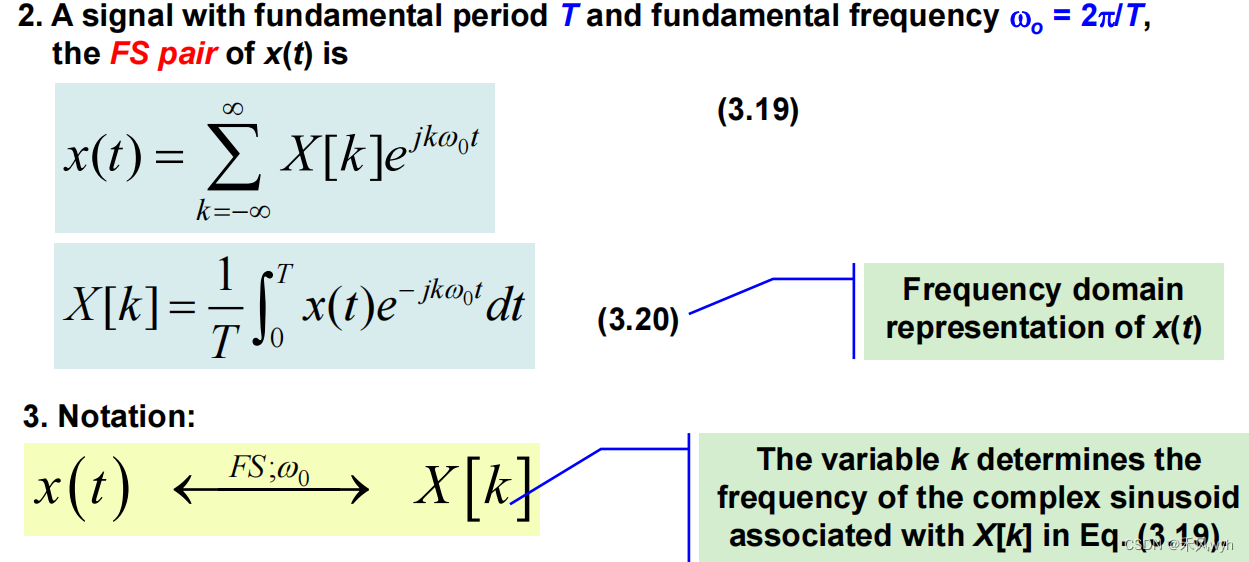
X [0]等于一个周期的平均值,是x(t)的直流分量
2) Mean-square error (MSE)


狄利克雷条件(Dirichlet condition):
①在任何周期内,x(t)绝对可积;
②在任何有限区间内,x(t)具有有限个最大值和最小值;
③在任何有限区间内,x(t)具有有限个不连续点,并且每个连续点都必须是有限值;
注:狄利克雷条件只是充分条件而非必要条件
3) Fourier series pair ⎯ Trigonometric FS

B [0]等于一个周期的平均值,是x(t)的直流分量
4) Determining CTFS Coefficients
①直接求算
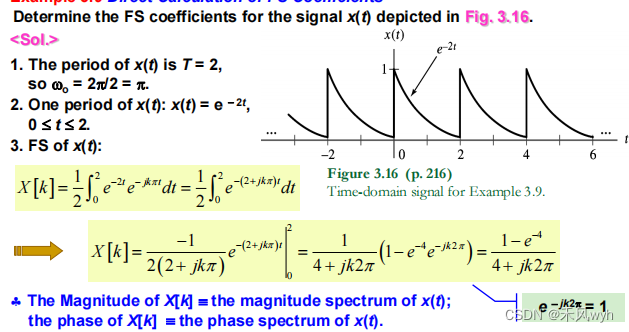
②基于冲激序列的信号

③观测法-正弦信号
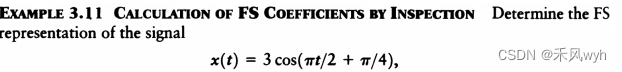


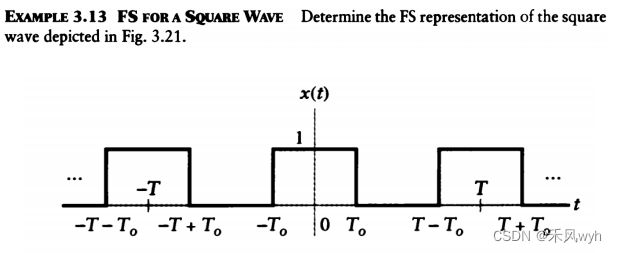
④方波
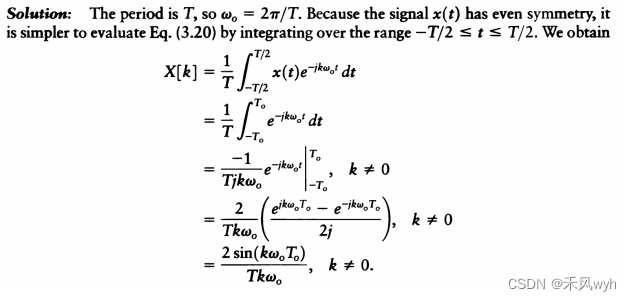

(5)离散时间非周期信号:离散时间傅里叶变换 DT Nonperiodic Signals: The DT Fourier Transform (DTFT)


(6)连续时间非周期信号:傅里叶变换 CT Nonperiodic Signals: The CT Fourier Transform (CTFT)
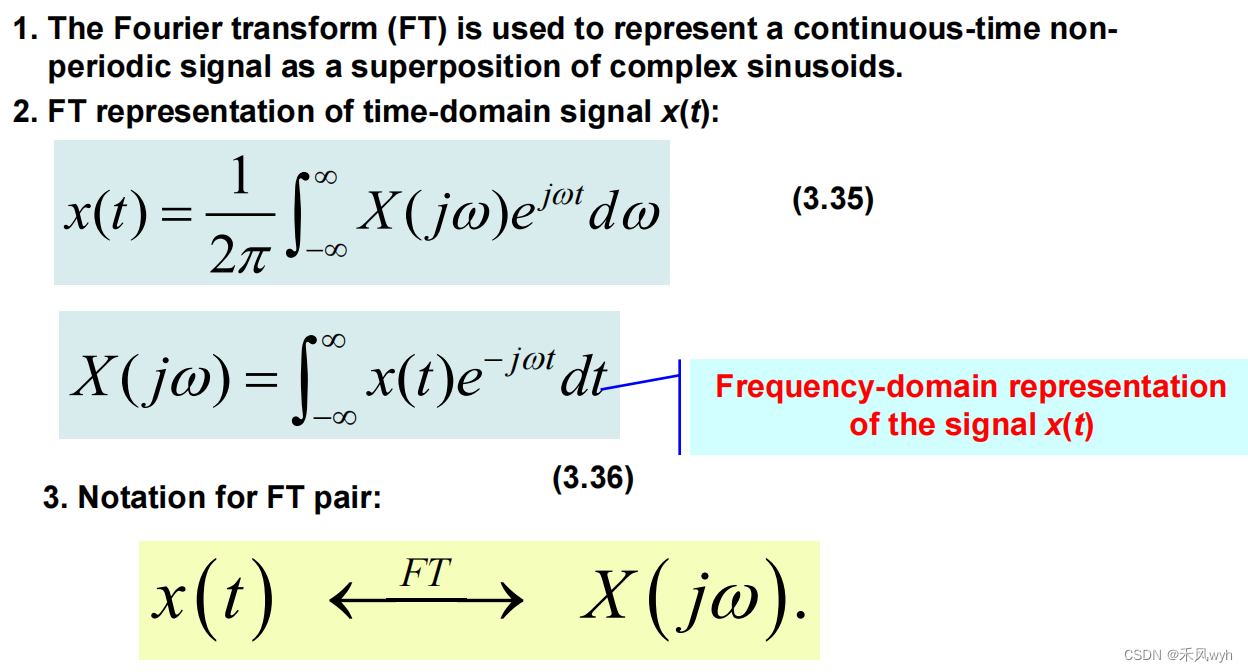


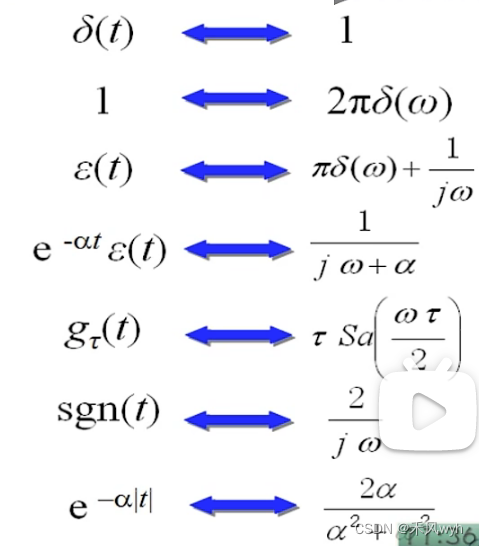
(7)常用信号的的傅里叶变换
1)单边指数函数 Real Decaying Exponential
①分类讨论,根据Dirchlet条件判断未知量的取值范围
②利用定义求解


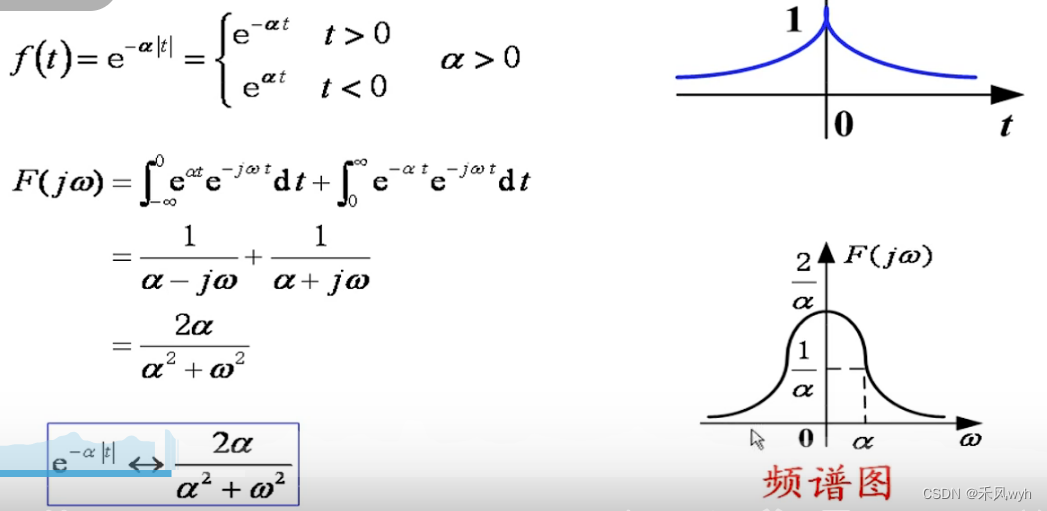
2)双边指数函数
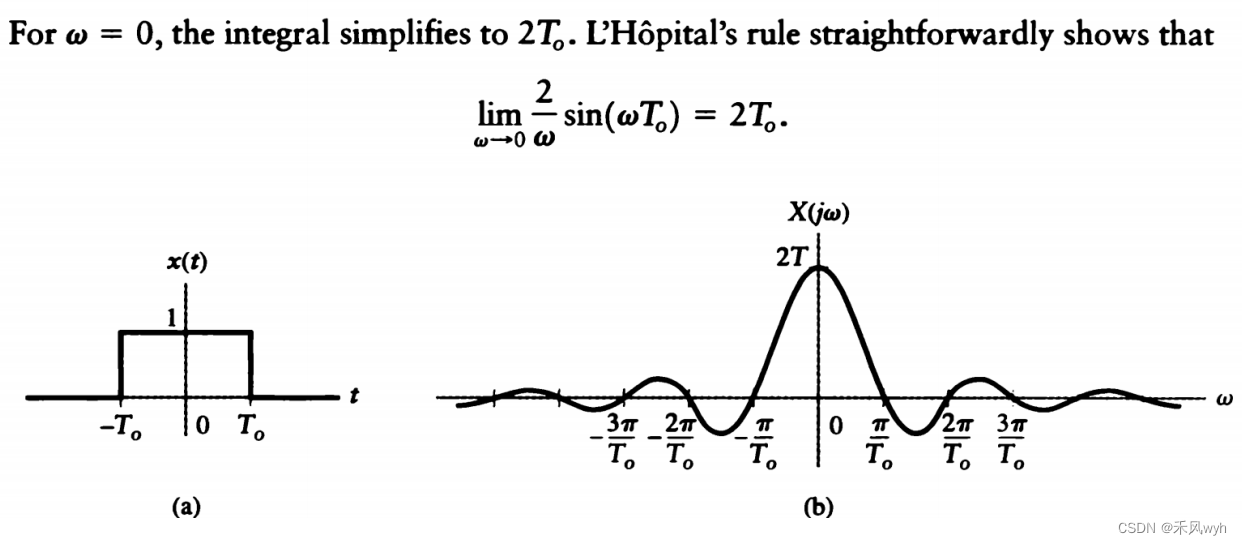
3)门函数(矩阵脉冲)Rectangular Pulse
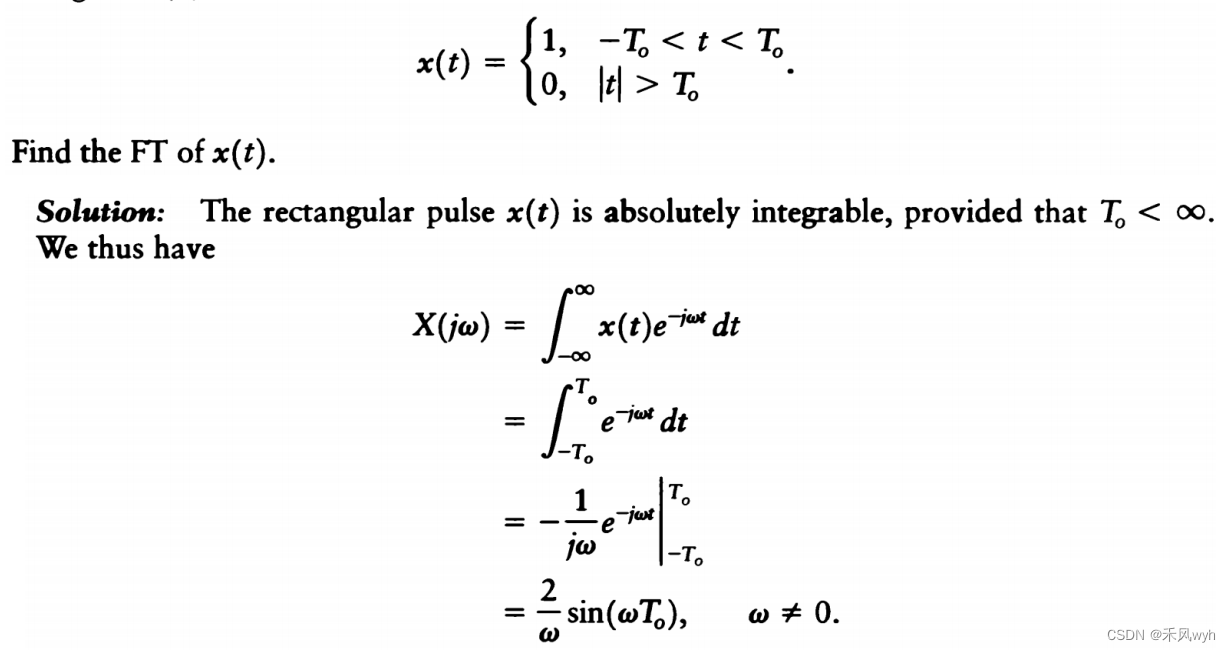

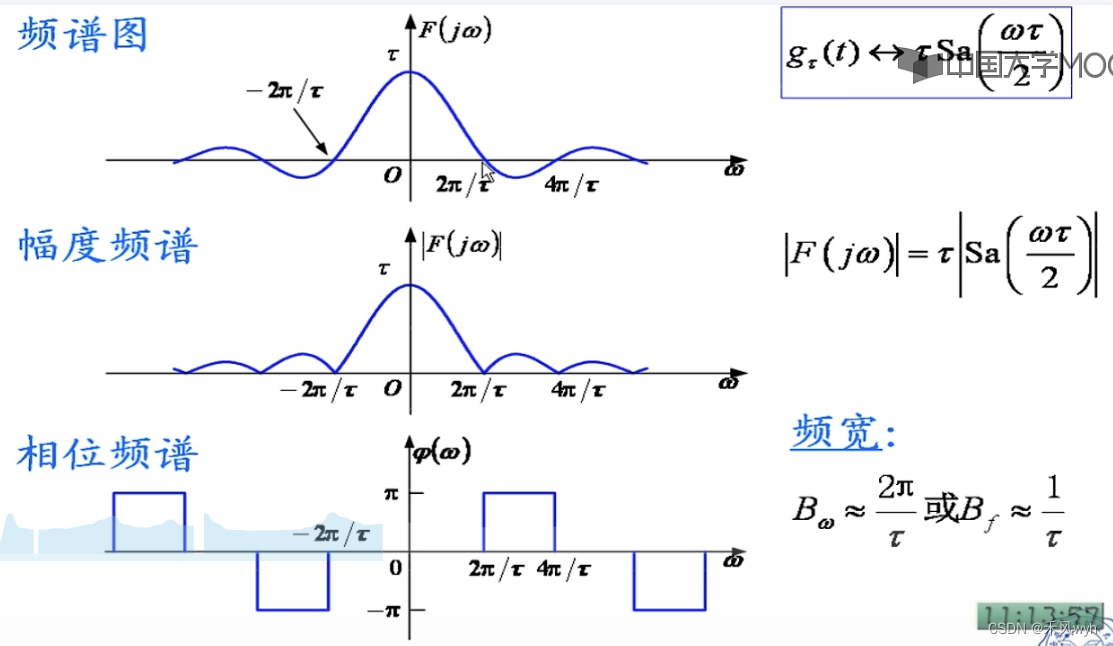
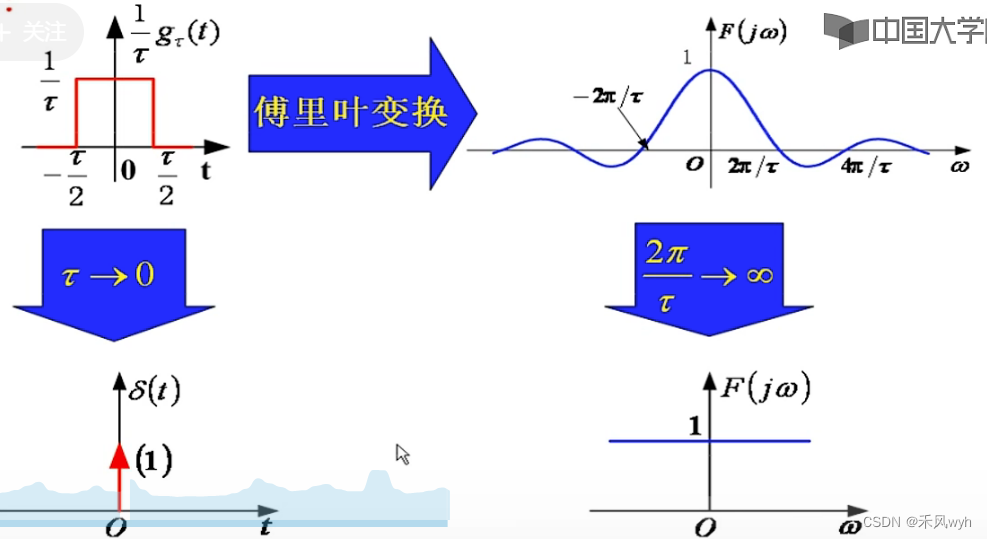
4)冲激函数
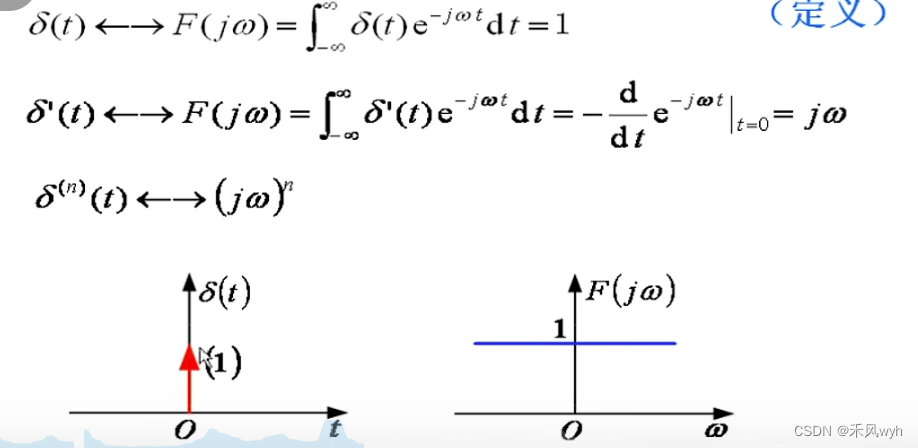


5) 符号函数

6)阶跃函数
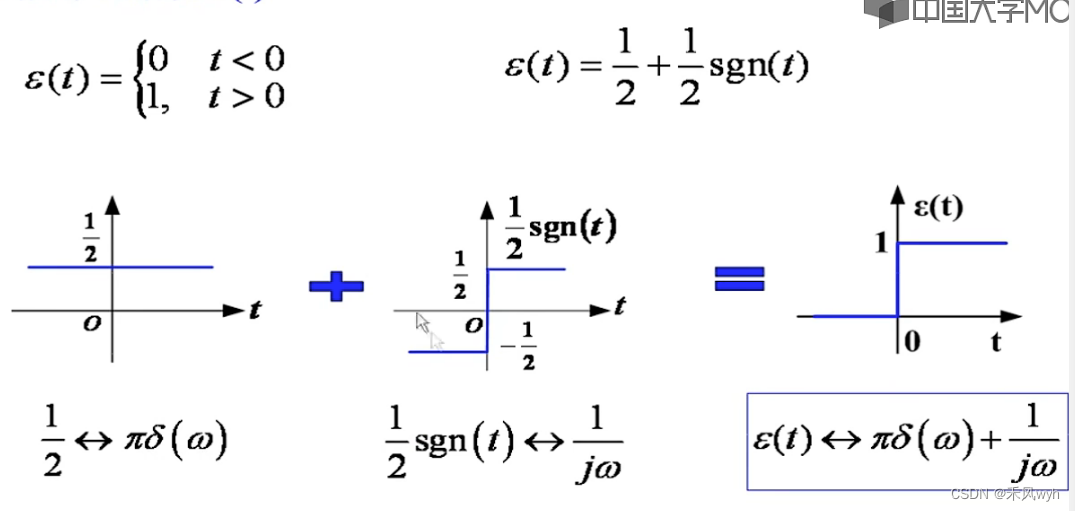
3、傅里叶表示的特性

4、傅里叶变换的性质
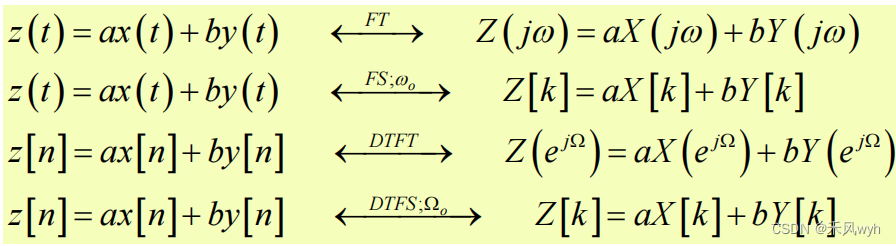
(1)线性性质
4种傅里叶表示
例1:阶跃信号
例2:
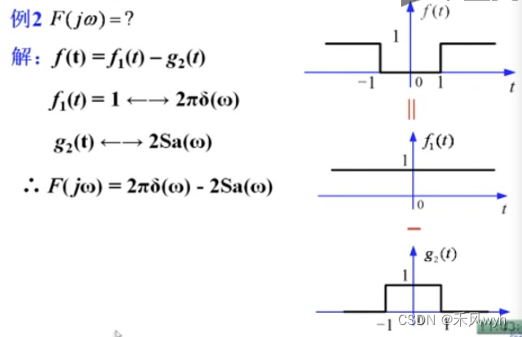
例3:方波
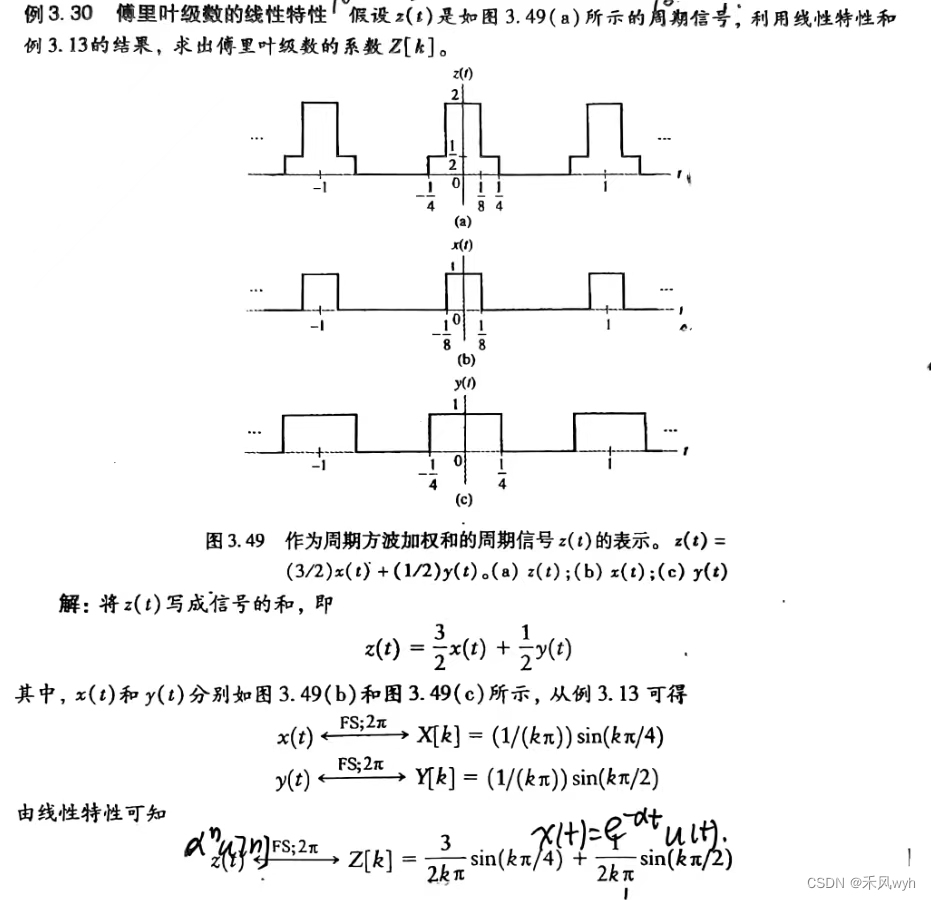
(2)对称特性Symmetry Properties
1) 实信号和虚信号 Real and Imaginary Signals
① Symmetry property for real-valued signal x(t)

The magnitude spectrum(模值) :even function
The phase spectrum (幅角值):odd function.
② Symmetry property for x(t) is purely imaginary

The magnitude spectrum(模值) :even function
The phase spectrum (幅角值):odd function
③ The conjugate symmetry property for DTFS
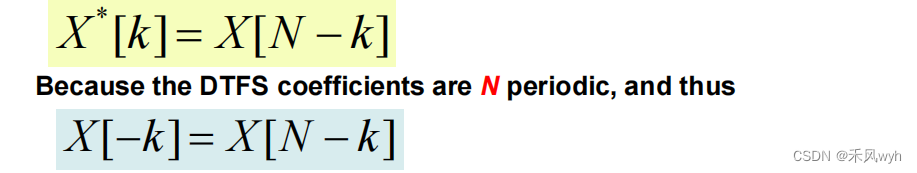
Conclusions:
If x(t) is real valued, then the real part of the transform is an even function of frequency, while the imaginary part is an odd function of frequency.
This also implies that the magnitude spectrum is an even function while the phase spectrum is an odd function

2)偶信号与奇信号 Even and Odd Signals


实偶函数:X*(jw)=X(jw)
实奇函数:X*(jw)=-X(jw)
(3)卷积特性
1)非周期信号的卷积 Convolution of Nonperiodic Signals — Continuous-time case
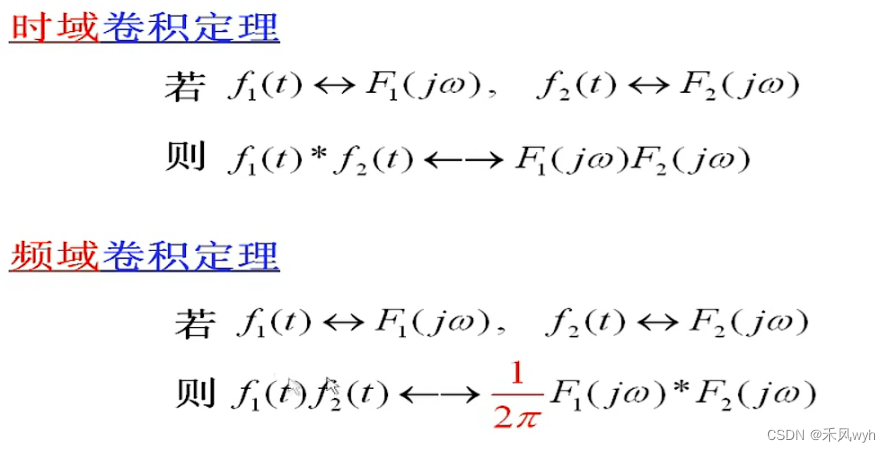


2) 滤波 Filtering
① 概念
频域上的相乘 Multiplication in frequency domain
② 表示
滤波表示输入信号的一些频率分量被滤除,而其他的频率分量无改变地通过系统
The terms “filtering” implies that some frequency components of the input are eliminated while others are passed by the system unchanged
③ 滤波的系统类型System Types of filtering
a. Low-pass filter
衰减信号的高通分量而通过低通分量
b. High-pass filter
衰减信号的低通分量而通过高通分量
c. Band-pass filter
允许特定频带范围的信号通过
④ 实际滤波器 Realistic filter
a. Gradual transition band
过渡带,过渡过程的频率范围
b. Nonzero gain of stop band
阻带无法做到零增益
⑤滤波器的幅度相应 Magnitude response of filter

⑥通带的边缘The edge of the passband
通带的边缘通常由响应为−3 dB的频率定义,对应的响应幅度为 1/ 2^(1/2)
The edge of the passband is usually defined by the frequencies for which the response is −3 dB, corresponding to a magnitude response of 1/ 2^(1/2)
Unity gain = 0 dB
⑦ 滤波器能谱Energy spectrum of filter
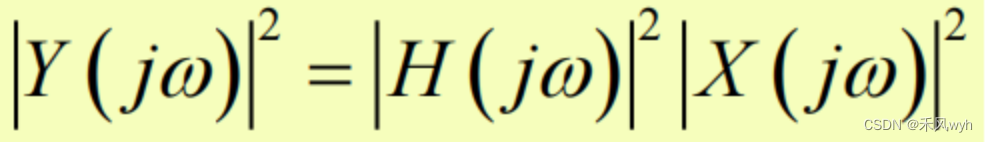
−3 dB点对应于滤波器只通过一半输入功率的频率
The −3 dB point corresponds to frequencies at which the filter passes only half of the input power.
− 3 dB point==Cutoff frequency
⑧ The expression of frequency response
The convolution property implies that the frequency response of a system may be expressed as the ratio of the FT or DTFT of the output to the input
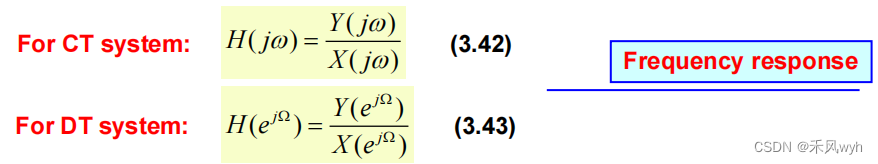

⑨从输出中恢复系统的输入Recover the input of the system from the output
a. 逆系统也称为均衡器,从输出中恢复输入的过程称为均衡器
An inverse system is also known as an equalizer, and the process of recovering the input from the output is known as equalization.
b. 因果限制→一个精确的逆系统是很难或不可能实现的!
Causality restriction → An exact inverse system is difficult or impossible to be implemented!

3)周期信号的卷积 Convolution of Periodic Signals
a. 公式

b. Convolution in Time-Domain<-> Multiplication in Frequency-Domain
4)Summary

(4)微积分特性 Differentiation and Integration Properties
1) 时域微分Differentiation in Time

Differentiation of x(t) in Time-Domain<-> (jw) x X(jw) in Frequency-Domain
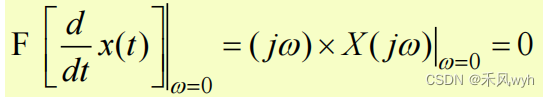
2) 时域积分Integration in Time

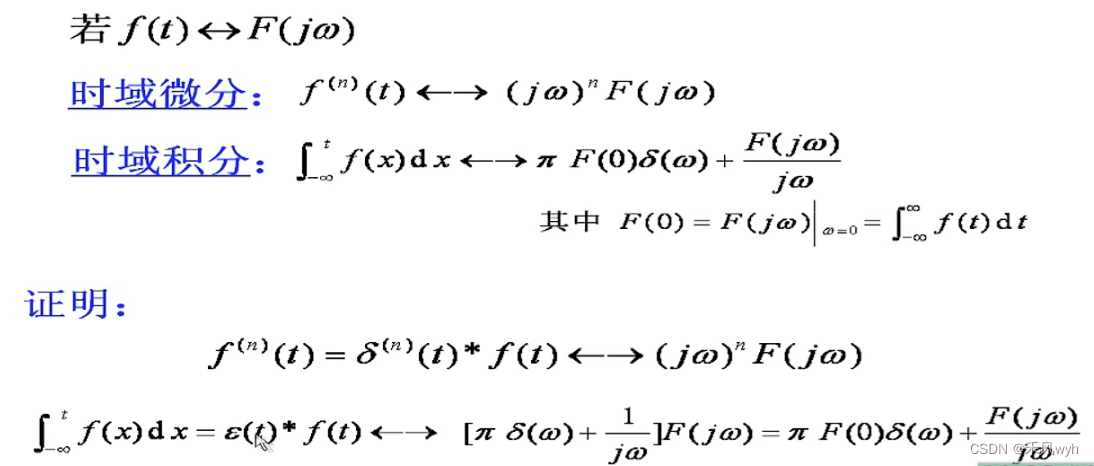

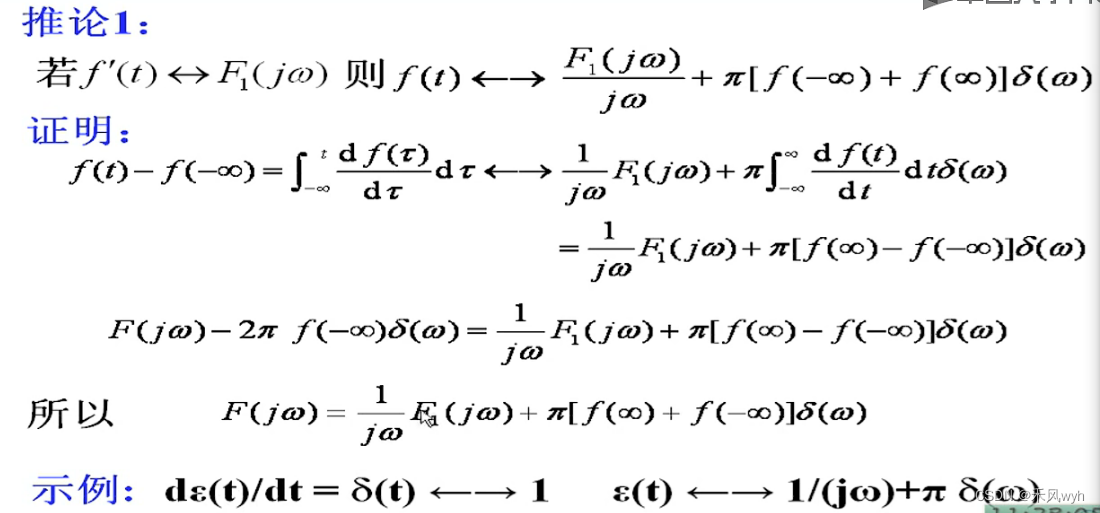
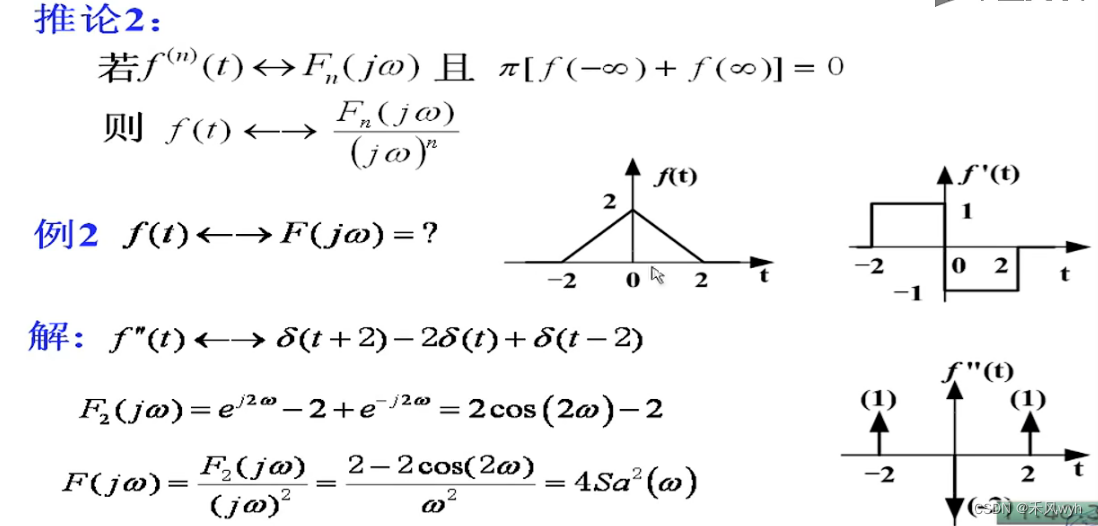
3) 频域微积分Differentiation in Frequency

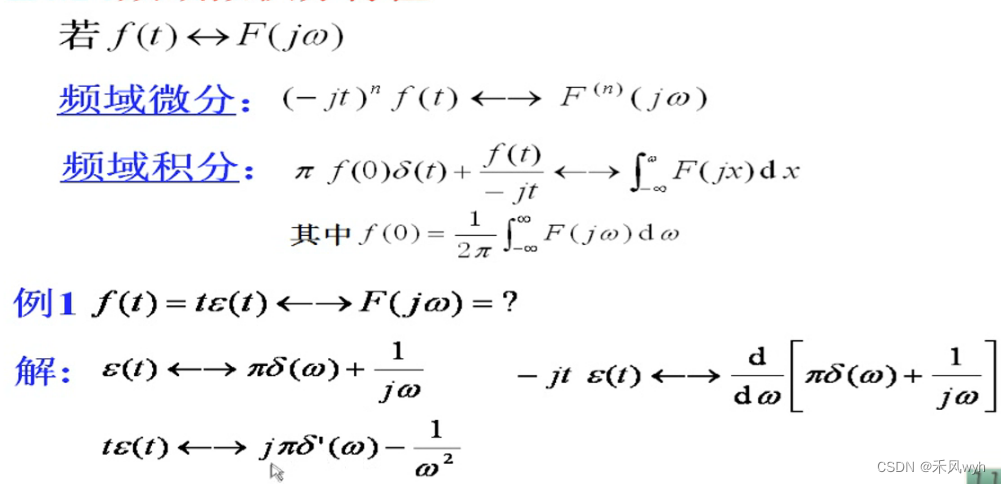

4)Summary

(5)时移和频移特性
1)时移特性
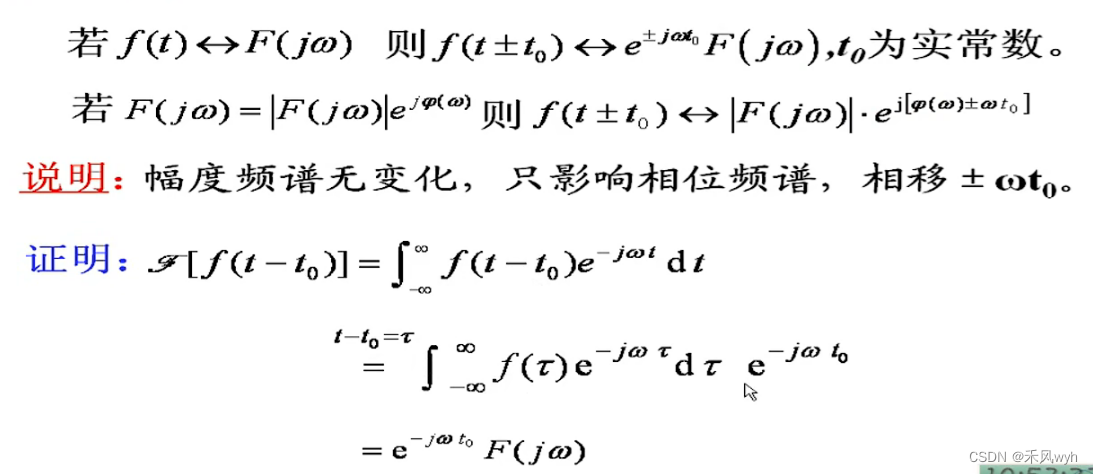




2)频移特性
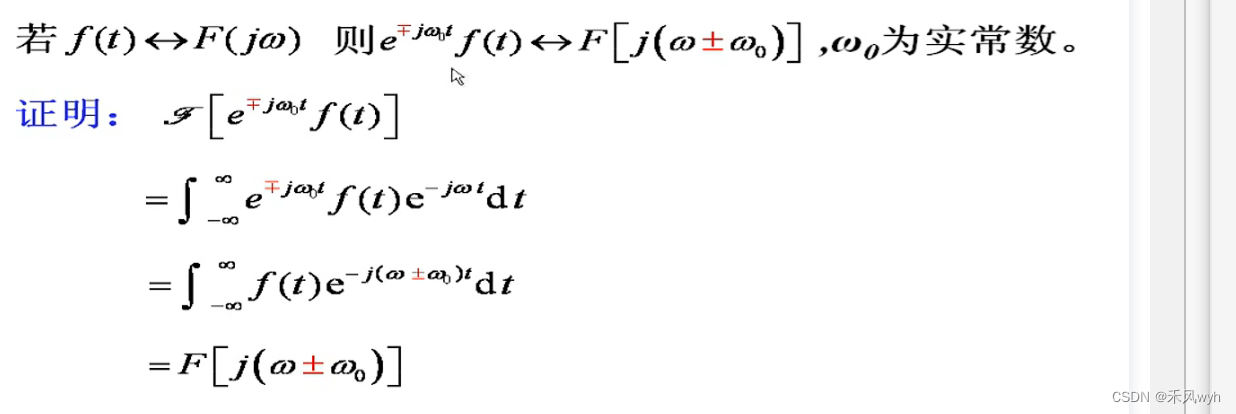

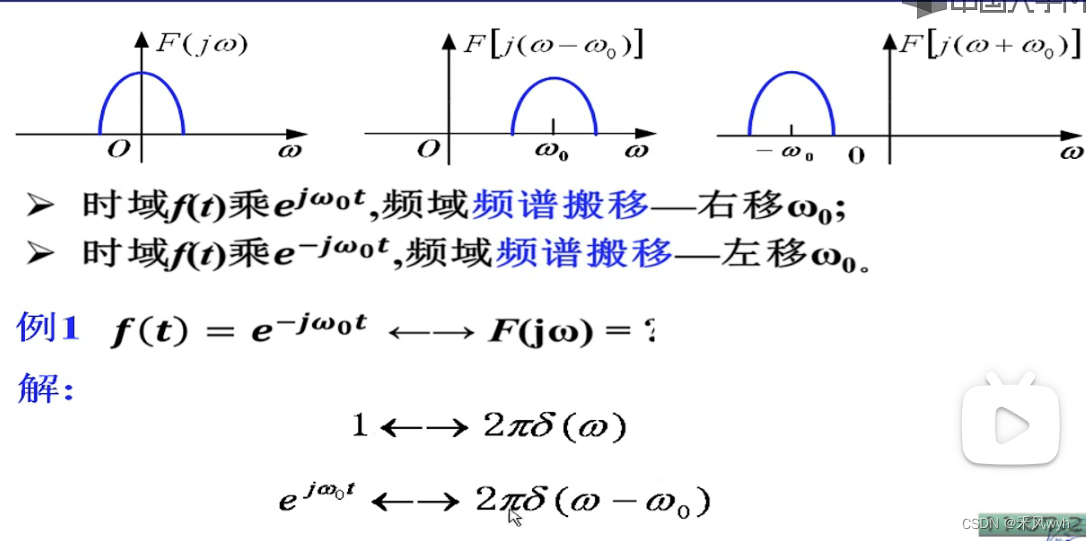
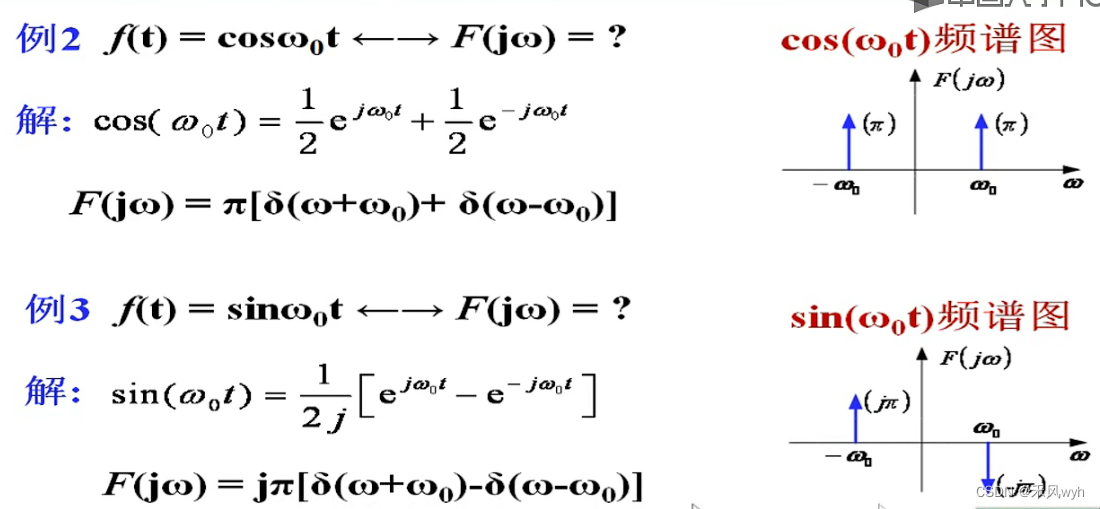
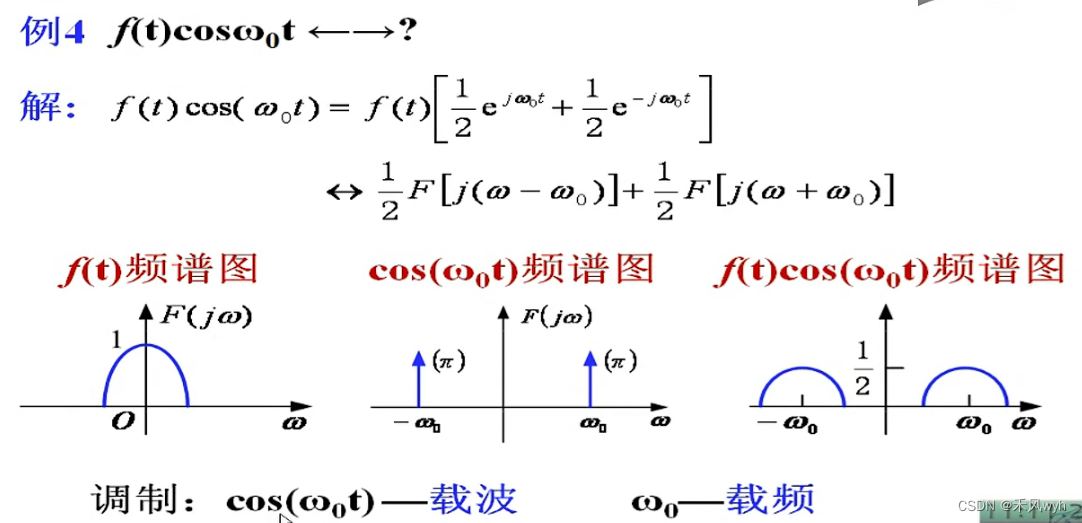
(6)相乘特性 Multiplication Property
1)Non-periodic continuous-time signals

2) Non-periodic discrete-time signals

3)乘法特性可以用来研究截断时域信号对其频率域的影响
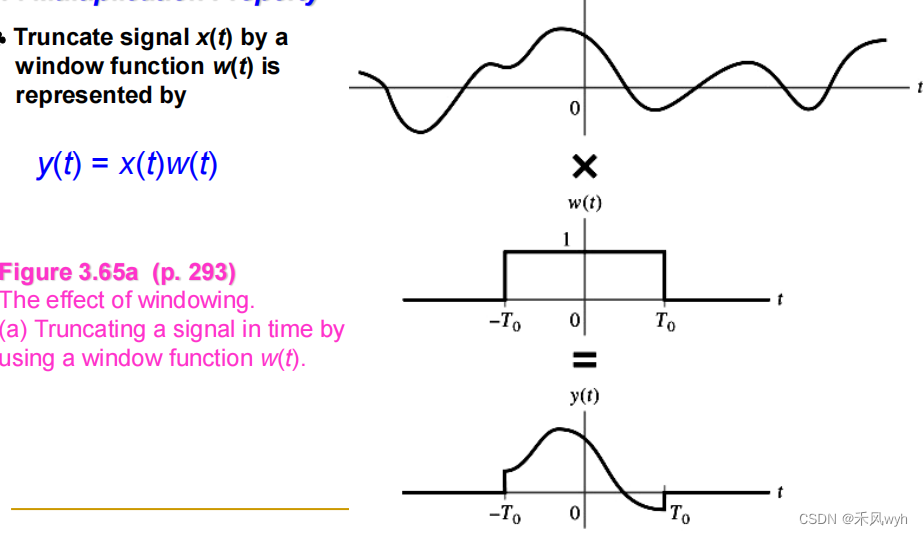
(7) 尺度变换特性 Scaling Property
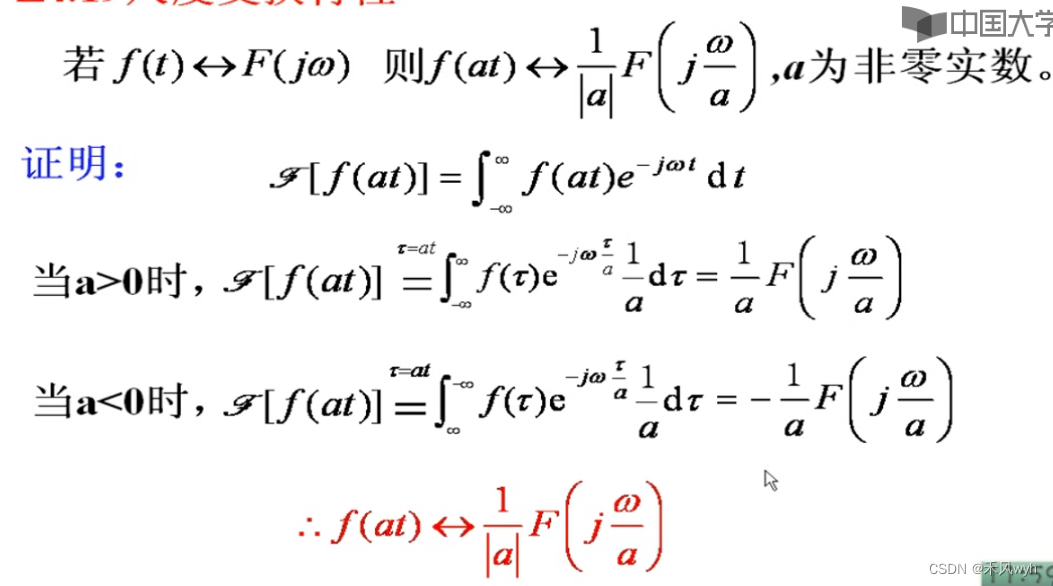
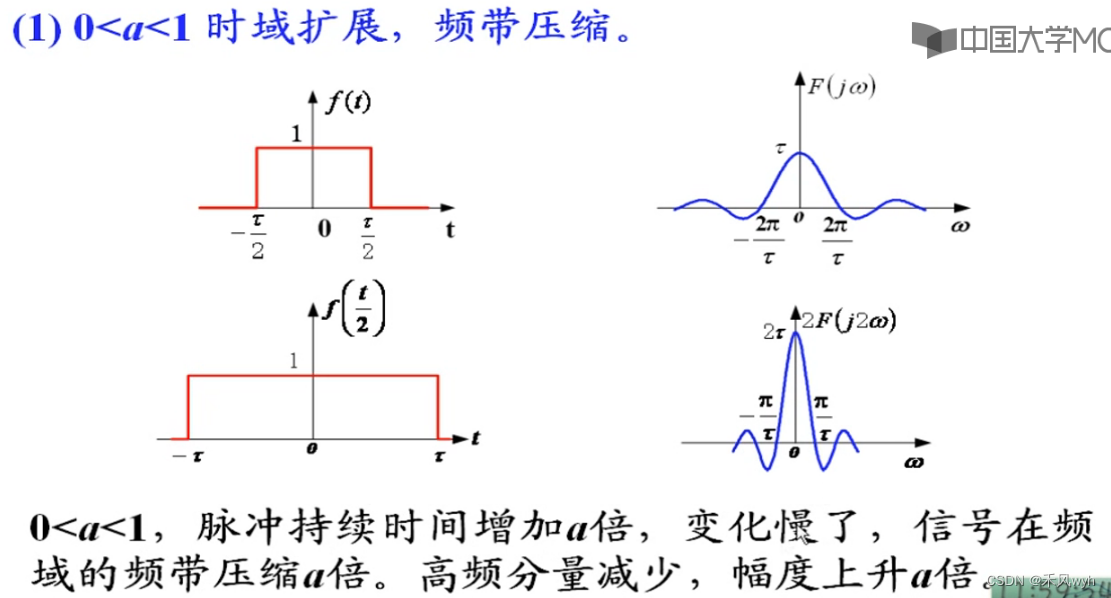
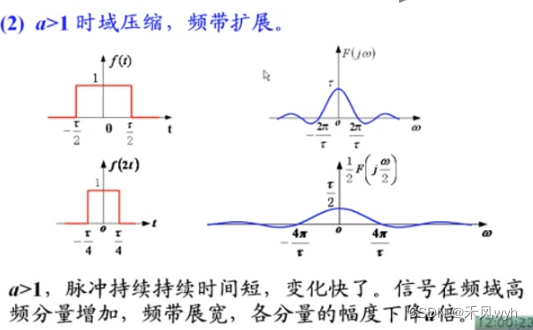
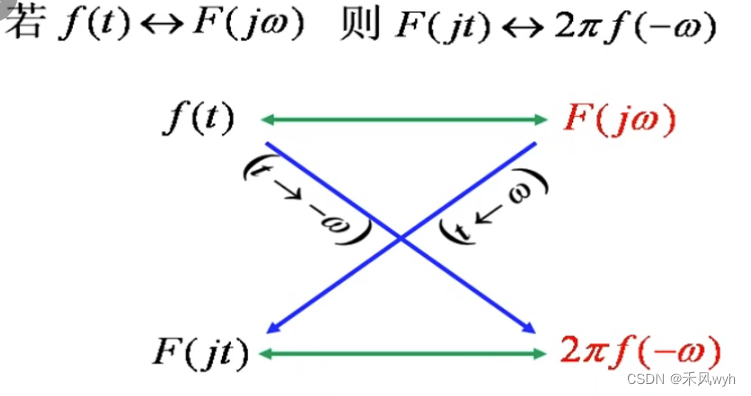
(8) 对称互易特性

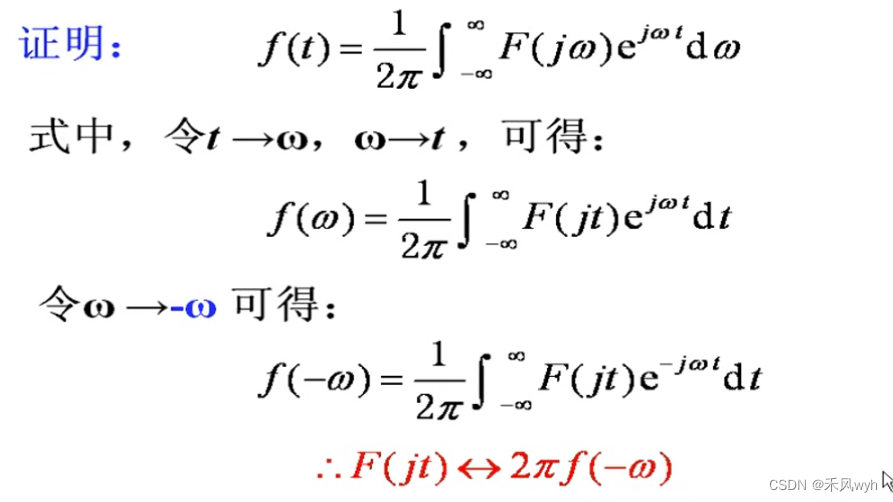
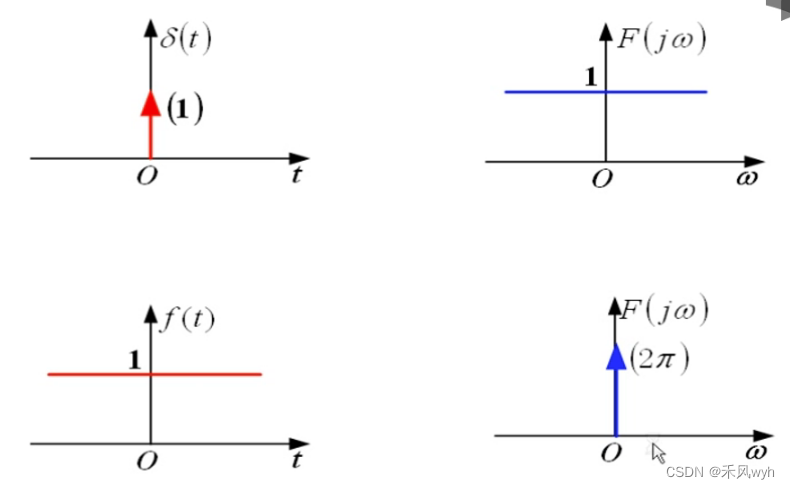
例题1:

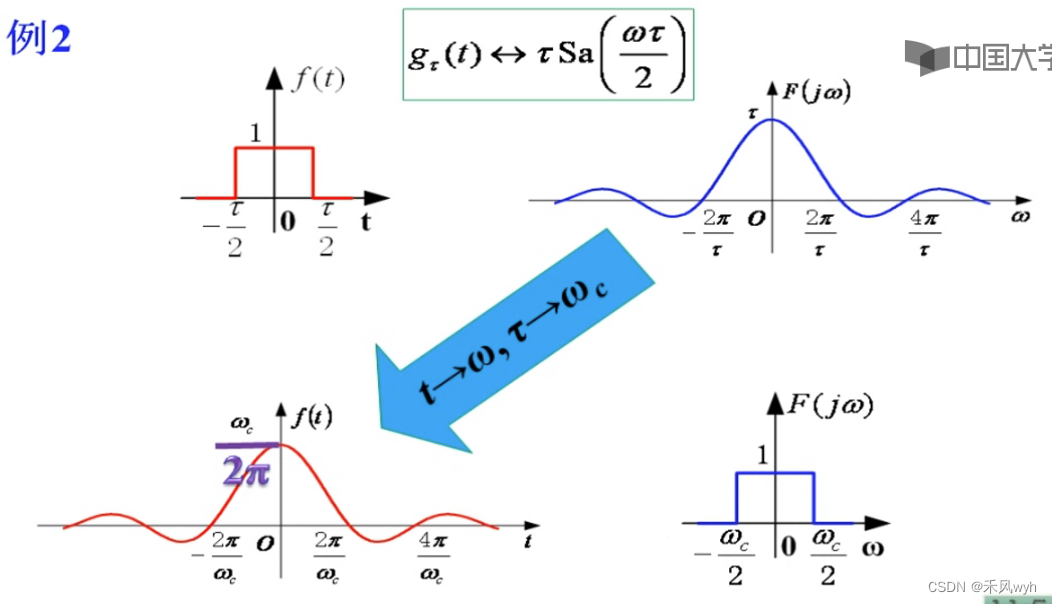
例题2
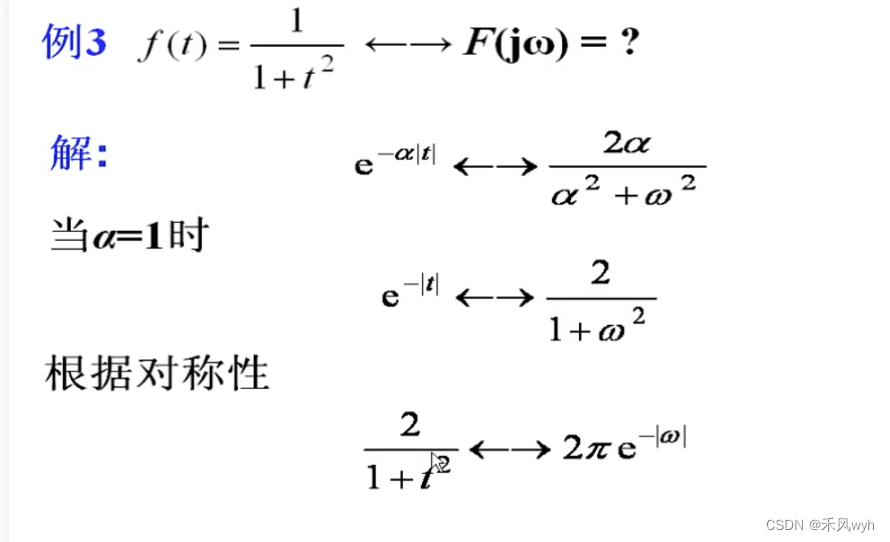
例题3
(9)相关定理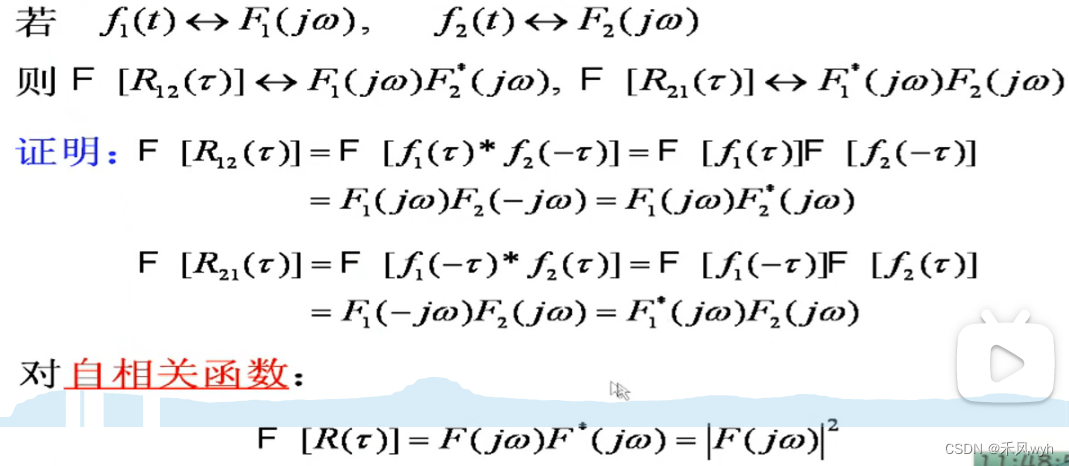
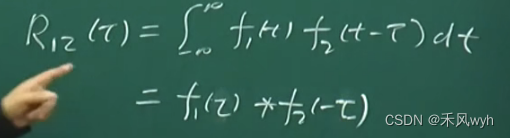
5、帕斯瓦尔定理 Parseval Relationships
(1)能量信号

(2)Parseval Relationships
The energy or power in the time-domain representation of a signal is equal to the energy or power in the frequency-domain representation.

1)CT nonperiodic signal
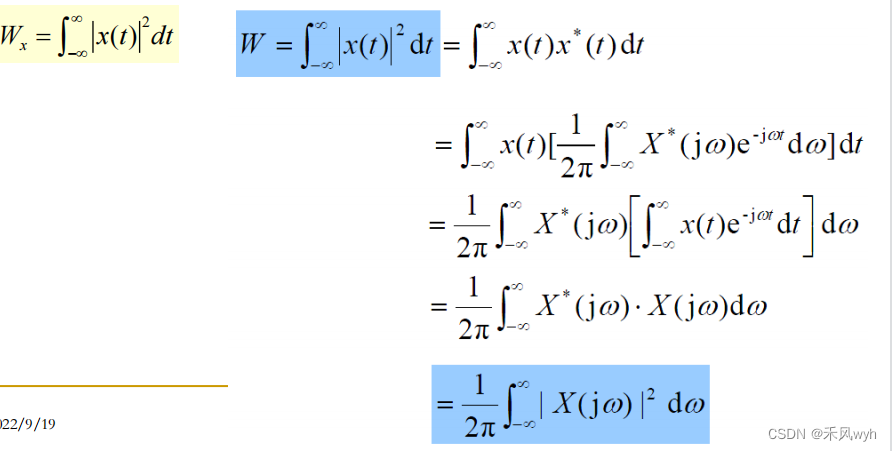
2)Energy in Time-Domain Representation–Energy in Frequency-Domain Representation x (1/2Π)

3)能量谱
①能量信号的定义
单位频率的信号能量
②物理意义
为了表征能量在频域中的分布情况而定义的能量密度函数,简称为能量频谱或能量谱
③公式

④能量有限信号的能量谱E(w)与自相关函数R(t)是一对傅里叶变换
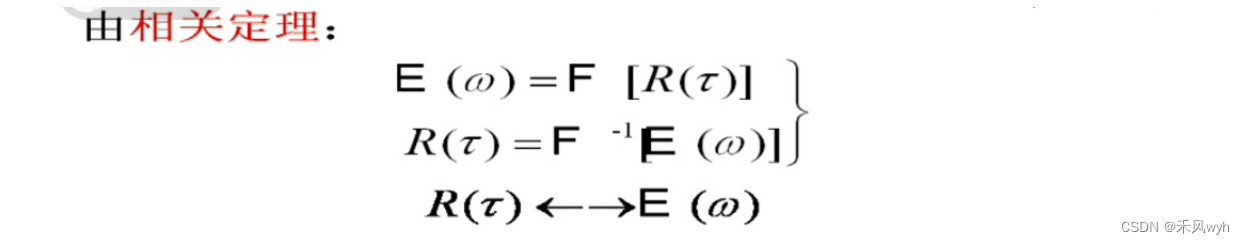

信号的能量谱E(w)是w的偶函数,它只取决于频谱函数的模量,而与相位无关。

4)功率谱
① 功率信号的定义
单位频率的信号功率
②平均功率
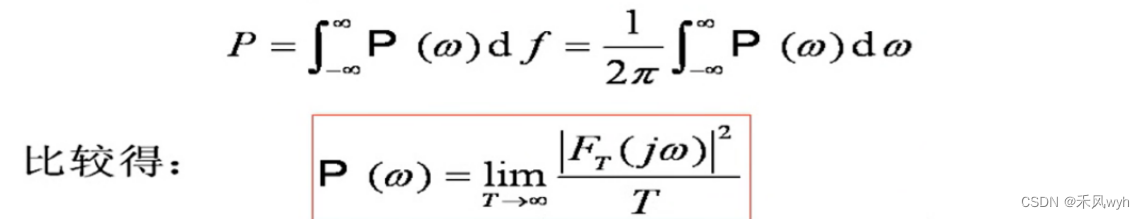
信号的功率谱P(w)是w的偶函数,它只取决于频谱函数的模量,而与相位无关
③功率有限信号的功率谱P(w)与自相关函数R(t)是一对傅里叶变换
若f1(t)和f2(t)是功率有限信号,此时相关函数的定义为
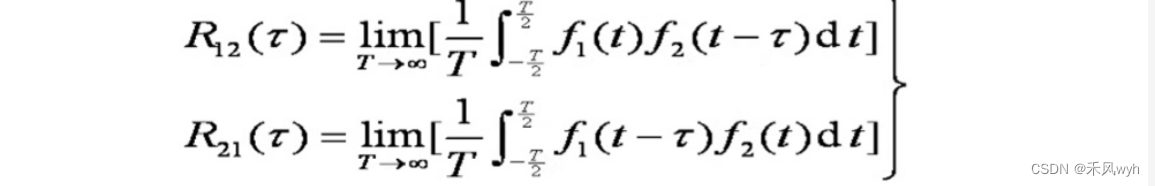
自相关函数为
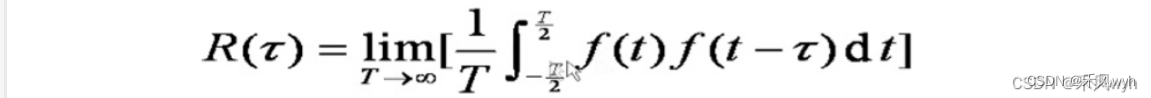
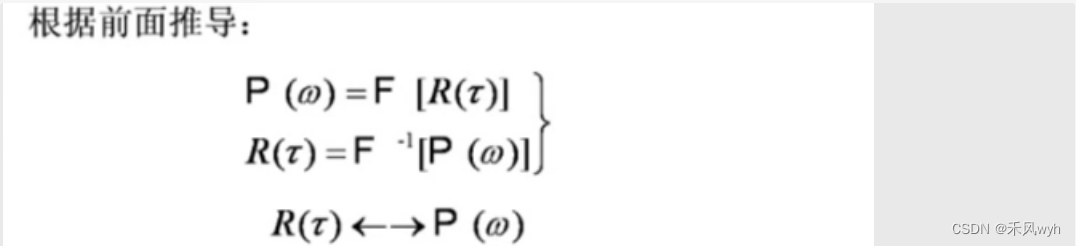



6、时间带宽积 Time-Bandwidth Product
1) 方波信号
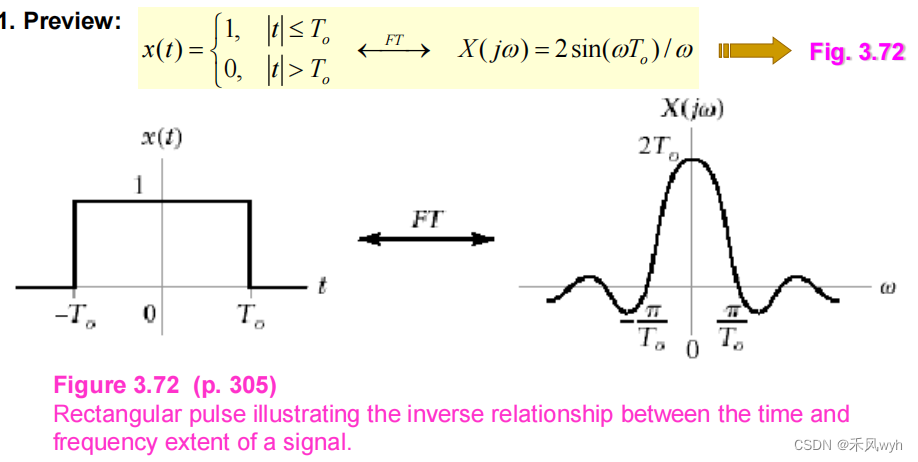
2)相关概念
① 时域和频域函数的取值范围
x (t)的时间范围为2To,X(jw)实际上是无限范围的频率。
② 能量
sinc函数的主叶下降在 |w|<Π/To 区间,其中包含了它的大部分能量。
③ 常数
时间范围To与主瓣宽度2Π/To的乘积是一个常数。
④频域时域关系
在时间上压缩一个信号会导致频域内的膨胀,反之亦然。
⑤Bandwidth带宽
信号的显著频率内容的范围,空为界的主叶瓣。幅度谱为其峰值的1/2^(1/2)时的频率。
3)x(t)信号的有效持续时间 Effective duration of signal
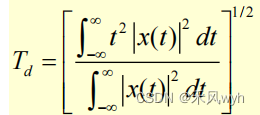
4) x(t)信号的有效带宽 Effective bandwidth of signal
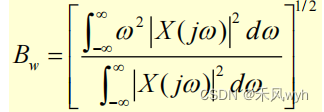
5)有界性
任何信号的时间带宽积都是下界的The time-bandwidth product for any signal is lower bounded according tothe relationship

6)测不准原理Uncertainty principle
我们不能同时减少一个信号的持续时间和带宽。