《从零开始：机器学习的数学原理和算法实践》chap6

《从零开始：机器学习的数学原理和算法实践》chap6 学习笔记

文章目录

- 6.1 凸函数
- 6.2 梯度下降
- - 引入
  - 梯度是什么
  - - 为啥梯度是上升最快的方向捏
  - 梯度下降与参数求解
  - 梯度下降过程演示
- 6.3 代码实践梯度下降
- - 一元函数的梯度下降
  - 多元函数的梯度下降

6.1 凸函数

凸集
- 何为凸集
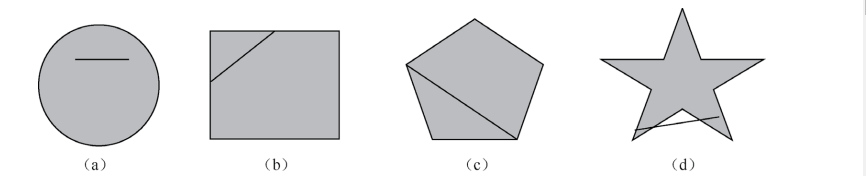
  - 凸集表示一个欧几里得空间中的区域，这个区域具有如下特点：区域内任意两点之间的线段都包含在该区域内；更为数学化的表述为，集合 C 内任意两点间的线段也均在集合 C 内，则称集合 C 为凸集
  - 常见图形示例
凸函数
- 如果某函数的上镜图（函数曲线上的点和函数曲线上方所有的点的集合）是凸集，那么该函数就是凸函数。
我记得这里有些地方定义不同 👇，去查了查
- 为什么不同教材中凸函数和凹函数的定义是不同的? 知乎 https://www.zhihu.com/question/31160556/answer/50926576
- 算了算了，都是凸的，上凸下凸，还有头秃（bushi）
- wiki百科关于凹凸函数的定义
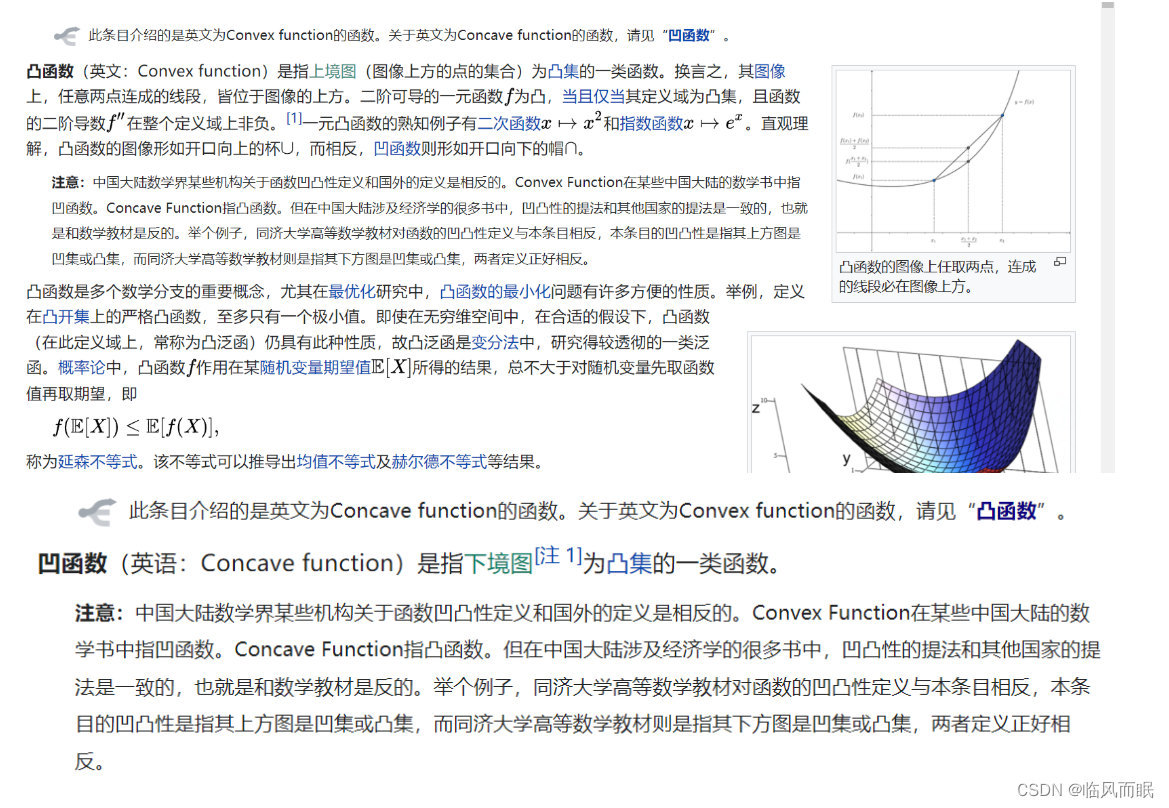
机器学习”热爱“凸函数

6.2 梯度下降

引入

很多机器学习算法都可归结为凸优化问题的求解，因此凸优化问题在机器学习中具有特别重要的地位，而梯度下降法是最简单、也是最常见的一种最优化问题求解方法。
机器学习中一般将凸优化问题统一表述为函数极小值求解问题，即 $min{f(x)}$ 。其中 x 是需要被优化的变量，f 为目标函数。
- 如果碰到极大值问题，则可以将目标函数加上负号，从而将其转换成极小值问题来求解。
- 目标函数的自变量 x 往往受到各种约束，满足约束条件的自变量 x 的集合称为自变量的可行域。
以山作比
- 梯度下降法是一种逐步迭代、逐步缩减损失函数值，从而使损失函数值最小的方法。
- 如果把损失函数的值看作一个山谷，我们刚开始站立的位置可能是在半山腰，甚至可能是在山顶。但是，只要我们往下不断迭代、不断前进，总可以到达山谷，也就是损失函数的最小值处。
- 例如，假设一个高度近视的人在山的某个位置上（起始点），需要从山上走下来，也就是走到山的最低点。这个时候，他可以以当前位置点（起始点）为基准，寻找这个位置点附近最陡峭的地方，然后朝着山的高度下降的方向走，如此循环迭代，最后就可以到达山谷位置。
- 首先，选择起始值（任意参数 $\omega$ 和 $b$ ), 由此得到损失函数的起始值
- 其次，明确迭代方向，逐步迭代
  - 我们站在半山腰或者山顶，环顾四周，找到一个最陡的方向下山，也就是直接指向山谷的方向下山，这样下山的速度是最快的。这个最陡在数学上的表现就是梯度，也就是说沿着负梯度方向下降能够最快到达山谷
- 最后确定迭代步长
  - 如果步长太大，虽然能够更快逼近山谷，但是也可能由于步子太大，踩不到谷底点，直接就跨过了山谷的谷底，从而造成来回振荡。
  - 如果步长太小，则延长了到达山谷的时间。所以，这需要做一下权衡和调试

梯度是什么

梯度的本质是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率（该梯度的模）最大。一般来说，梯度可以定义为一个函数的全部偏导数构成的向量。总结来说有如下两种情况
- 在单变量函数中，梯度就是函数的导数，表示函数在某个给定点的切线斜率，表示单位自变量变化引起的因变量变化值
- 在多变量函数中，梯度就是函数分别对每个变量进行微分的结果，表示函数在给定点上升最快的方向和单位自变量（每个自变量）变化引起的因变量变化值
梯度是一个向量，它的方向就是函数在给定点上升最快的方向，因此负梯度方向就是函数在给定点下降最快的方向。一旦我们知道了梯度，就相当于知道了凸函数下降最快的方向

为啥梯度是上升最快的方向捏

这需要用到方向导数的概念，下面这几个我觉得写的不错
- 为什么梯度反方向是函数下降最快的方向？
- 梯度的方向为什么是函数值增加最快的方向？知乎 https://zhuanlan.zhihu.com/p/38525412
我想尝试用直观的角度来理解
- 很多例子用下山，说下山走最陡的方向，但是怎么判断最陡峭呢？
- 我尝试用 $z=x^2+y^2$ ，从物理上矢量合成的角度来不严谨地解释一下
  - 如图是 $z=x^2+y^2$ ，每个点有x方向的偏导数和y方向的偏导数
    - 对于一元函数z=f(y)和z=f(x)来说，每个点都可以往两个方向去变化，就是往直线的一端去或者直线的另一端去，
    - 而当变成了二元函数，就可以往四面八方去了
      
      偏导数组成了向量{2x，2y}，那这个变化率用矢量合成我们可以这样来看
      
      可以看成提供了2x,-2x,2y,-2y合成的四个方向基本的力，拉着自己在山上动，
      
      假设我们要从x>0，y>0那块区域上山，我们在x方向和y方向上的变化率分别为在这两个方向的偏导数，可以由图比较明显的看到，要往上走得快，那应该是x方向要往x变大的方向，y方向上也应该是往y变大的方向
      
      那么很显然，2x和2y由平行四边形法则合成的矢量方向是很合适的，上升最快的
      
      而图中蓝色和红色方向上提供的力都没有那么大（呜呜很不严谨，也不知道说的对不对）
      
      反过来，-2x和-2y合成的那个向量就是下降最快的方向
      
      这段话没有组织好😭… 感觉自己想表达的意思没表达出来而且说的很乱呜呜呜，等想好了再来更新

关于泰勒公式和梯度下降
- https://mp.weixin.qq.com/s/k26Fm0GL3fdVA9VbQIVAuQ
- 从泰勒公式到梯度下降 - 知乎 https://zhuanlan.zhihu.com/p/144855529
- https://sm1les.com/2019/03/01/gradient-descent-and-newton-method/

梯度下降与参数求解

这个好像很多地方说法略有不同

梯度下降过程演示

梯度下降法中最重要的是如下的迭代式。

$\\\\\theta^{1}=\theta^{0}-a \nabla J(\theta)$

上述公式表示的含义是, 任意给定一组初始参数值 $\theta^{0}$ , 只要沿着损失函数$ J(\theta)$ 的梯度下降方向前进一段距离 a, 就可以得到一组新的参数值 $\theta^{1}$ 。这里的 $\theta^{0}$ 和 $\theta^{1}$ 对应到机器学习中就是指模型参数 (如 $\omega$ 和 $b$ )。
例

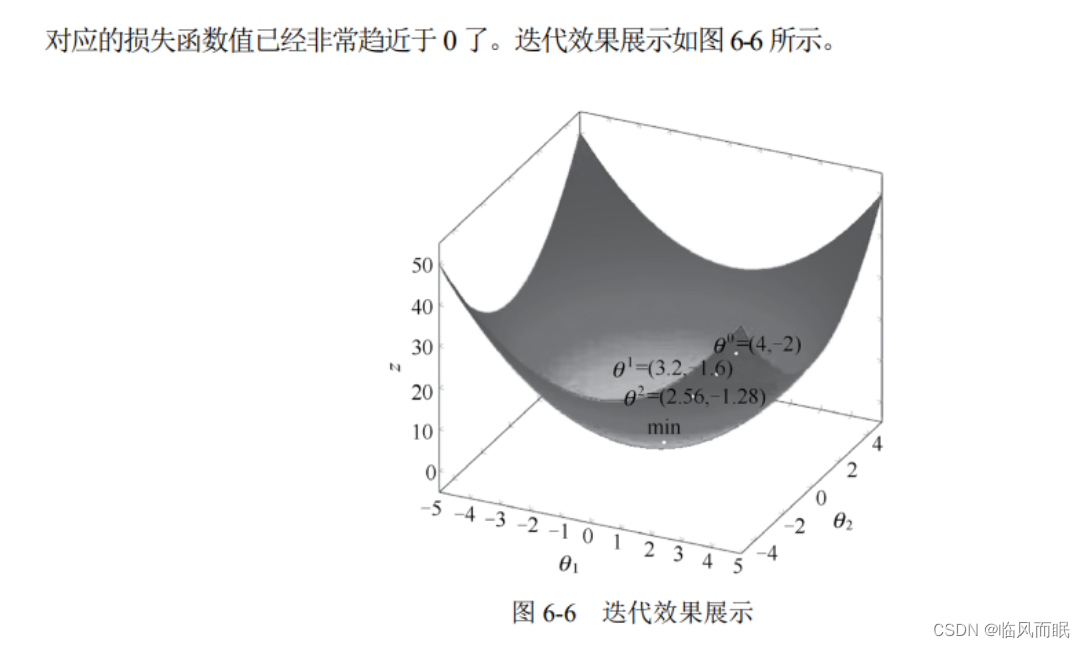
在这里插入图片描述

关于梯度下降法，迭代结束的常见情景有两种。
- 设置阈值。设置一个迭代结束的阈值，当两次迭代结果的差值小于该阈值时，迭代结束。
- 设置迭代次数。设置一个迭代次数（如200)，当迭代次数达到设定值，迭代结束。一般来说，只要这个迭代次数设置得足够大，损失函数最终都会停留在极值点附近。同时，采用这种方法我们也不用担心迭代次数过多会导致损失函数“跑过”极值点的情况，因为损失函数在极值点时函数梯度为0，一旦过了极值点函数梯度正负性就发生变化了，会使函数围绕极值点再次“跑回来”。所以，即使设置的迭代次数过大，最终结果也会在极值点处“徘徊”。

6.3 代码实践梯度下降

一元函数的梯度下降

import matplotlib. pyplot as plt
import mpl_toolkits.axisartist as axisartist
import numpy as np
#创建画布
fig = plt.figure(figsize=(8,8))
#使用axisartist.Subplot方法创建绘图区对象ax
ax = axisartist.Subplot(fig,111)
#把绘图区对象添加至画布
fig.add_axes(ax)
#使用set_visible方法隐藏绘图区原有所有坐标轴
ax.axis[:].set_visible(False)
#使用ax.new_floating_axis添加新坐标轴
ax.axis["x"] = ax.new_floating_axis(0,0)
#给x轴添加箭头
ax.axis["x"].set_axisline_style("->", size = 1.0)
ax.axis["y"] = ax.new_floating_axis(1,0)
#给y轴添加箭头
ax.axis["y"].set_axisline_style("->", size = 1.0)
#设置刻度显示方向，x轴为下方显示，y轴为右侧显示
ax.axis["x"].set_axis_direction("bottom")
ax.axis["y"].set_axis_direction("right")
#x轴范围为-10～10，且分割为100份
x=np.linspace(-10,10,100)
y=x**2+3
#设置x、y轴范围
plt.xlim(-12,12)
plt.ylim(-10,100)
plt.plot(x, y)
plt.show()


def grad_1(x):
  return x*2

def grad_descent(grad,x_current,learning_rate,precision,iters_max):
  for i in range(iters_max):
    print ('第',i,'次迭代x值为:',x_current)
    grad_current=grad(x_current)
    if abs(grad_current)<precision:
      break # 当梯度值小于阈值时，停止迭代
    else:
      x_current=x_current-grad_current*learning_rate
  print ('极小值处x为：' ,x_current)
  return x_current

if __name__=="__main__":
    grad_descent(grad_1,x_current=5,learning_rate=0.1,precision=0.000001,iters_max=10000)

上述梯度下降中设置的 x 初始值为 5，学习率即迭代步长为 0.1
- 当 x 初始值为 5 时，代价函数 $y=x^2 +3$ 的梯度为 2×5=10，学习率为 0.1。由于代价函数的梯度值为 10，因此代价函数在 x=5 时并非极小值点。虽然该点并非极小值点，但给了我们继续迭代的一个起始值。
- 代价函数沿着负梯度方向下降最快，迭代步长为 0.1，因此 x 迭代的距离为 -10×0.1=-1。
- 经过一次迭代后，x=5-1=4。此时代价函数的梯度为 2×4=8，学习率为 0.1。显然，在 x=4 处，代价函数仍然没有到达极小值点，于是继续迭代。
- 代价函数的 x 值沿着负梯度方向迭代 -8×0.1=-0.8，于是得到新的 x=4-0.8=3.2。如此继续……
- 我们设置的最大迭代次数为 10 000，也就是说如果迭代次数达到 10 000，代价函数仍然未能取到极小值，那么也要停止迭代过程，防止计算机无休止地迭代下去。本例中迭代至第 73 次时，梯度值小于我们设置的阈值 0.000 001，我们可以认为代价函数达到了极小值。于是，整个梯度下降过程停止

多元函数的梯度下降

import numpy as np
import matplotlib. pyplot as plt
import mpl_toolkits.mplot3d
x, y = np.mgrid[-2:2:20j,-2:2:20j] #测试数据
z=(x**2+y**2)#三维图形
ax = plt.subplot(111,projection='3d')
ax.set_title('f(x,y)=x^2+y^2') ;
ax.plot_surface(x,y,z,rstride=9,cstride=1,cmap=plt.cm.Blues_r)#设置坐标轴标签
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

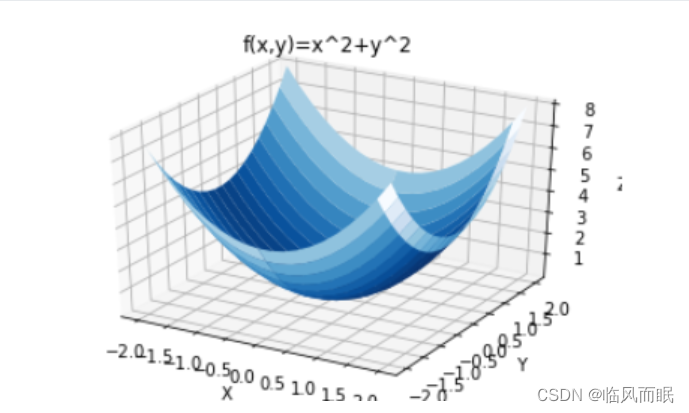
在这里插入图片描述

# 定义多元函数f(x,y)=x2+y2的梯度f'(x)=2x,f'(y)=2y， 
def grad_2(p):
      derivx = 2 * p[0]
      derivy = 2 * p[1]
      return np.array([derivx, derivy])
# 定义梯度下降函数 
def grad_descent(grad,p_current,learning_rate,precision,iters_max): 
     for i in range(iters_max):
          print ('第',i,'次迭代p值为:',p_current)
          grad_current=grad(p_current)
          if np.linalg.norm(grad_current, ord=2)<precision:
            break # 当梯度趋近于 0 时，视为收敛 
          else:
            p_current=p_current-grad_current* learning_rate 

     print ('极小值处p为：',p_current)
     return p_current
 #执行模块
if __name__=='__main__':
      grad_descent(grad_2,p_current=np.array([1,-1]),
      learning_rate=0.1,precision=0.000001,iters_max=10000)

在这里插入图片描述

上述梯度下降中设置的 p(x,y) 初始值为 [1,-1]，学习率即迭代步长为 0.1
- 当 p 初始值为 [1,-1] 时，代价函数 p(x,y)=$x^2 +y^2 $的梯度为向量 $[2 \times 1, 2 \times (- 1)]$ ，学习率为 0.1。由于代价函数的梯度的模大于 0，因此代价函数在 p=[1,-1] 时并非极小值点。虽然该点并非极小值点，但给了我们继续迭代的一个起始值。
- 代价函数沿着负梯度方向下降最快，迭代步长为 0.1，因此 x 迭代的距离为 $- [2, - 2] \times 0.1 = - [0.2, - 0.2]$ 。
- 经过一次迭代后， $p = [1, - 1] - [0.2, - 0.2] = [0.8, - 0.8]$ 。此时代价函数的梯度为 $2 \times [0.8, - 0.8] = [1.6, - 1.6]$ ，学习率为 0.1。显然 $p = [0.8, - 0.8]$ 处，代价函数仍然没有到达极小值点，于是继续迭代。
- 代价函数的 p 值沿着负梯度方向迭代 $- [1.6, - 1.6] \times 0.1 = - [0.16, - 0.16]$ ，于是得到新的 $p = [0.8, - 0.8] - [0.16, - 0.16] = [0.64, - 0.64]$ 。如此继续……
  ,-2]× 0.1=-[0.2,-0.2]$。
- 经过一次迭代后， $p = [1, - 1] - [0.2, - 0.2] = [0.8, - 0.8]$ 。此时代价函数的梯度为 $2 \times [0.8, - 0.8] = [1.6, - 1.6]$ ，学习率为 0.1。显然 $p = [0.8, - 0.8]$ 处，代价函数仍然没有到达极小值点，于是继续迭代。
- 代价函数的 p 值沿着负梯度方向迭代 $- [1.6, - 1.6] \times 0.1 = - [0.16, - 0.16]$ ，于是得到新的 $p = [0.8, - 0.8] - [0.16, - 0.16] = [0.64, - 0.64]$ 。如此继续……
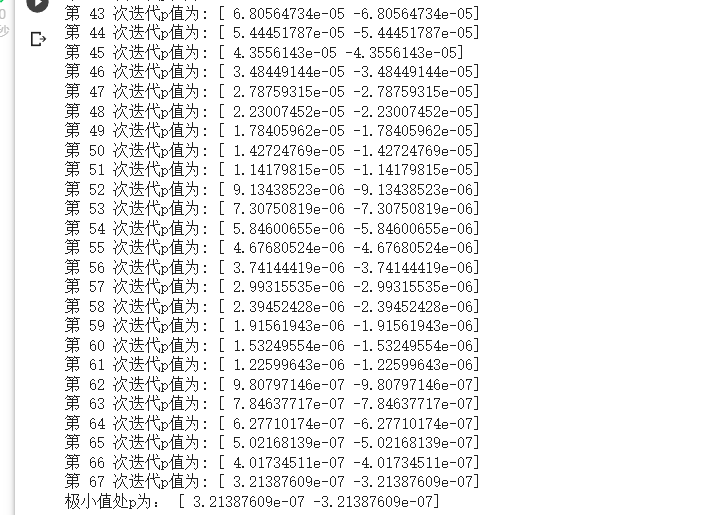
- 我们设置的最大迭代次数为 10 000，也就是说如果迭代次数达到 10 000，代价函数仍然未能取到极小值，那么也要停止迭代过程，防止计算机无休止地迭代下去。不过，本例中迭代至第 67 次时，梯度的模小于我们设置的阈值 0.000 001，我们可以认为代价函数达到了极小值。于是，整个梯度下降过程停止