质数：大于1，且只包含1和本身两个因数的整数

一、试除法判定质数

如果是合数，那么因数一定是成对出现的，比如12，有2*6=12，3*4=12，我们不用暴力枚举，从2一直枚举到n-1，我们只枚举成对出现的因数中较小的即可

比如当前数为n，有因数c和因数n/c，我们希望$c<=\frac{n}{c}$，并从2枚举到c，那c的范围就是$c<=\sqrt{n}$

bool isPrime(int n) {
	if (n < 2) {
		return false;
	}
	// 判断条件为i <= sqrt(n)，sqrt计算较慢，不推荐
	// 判断条件为i * i <= n，当n很接近INT_MAX时，i*i可能会大于INT_MAX，这就移除了，i*i变成负数，负数永远小于n，影响判断，不推荐
	for (int i = 2; i <= n / i; i++) {
		if (n % i == 0) {
			return false;
		}
	}
	return true;
}

时间复杂度一定是$O(\sqrt{n})$

二、试除法分解质因数

void divide(int n) {
	// 条件为i <= n，是暴力枚举n的因子
	for (int i = 2; i <= n / i; i++) {
		// 我们这里的i是否可能是合数呢？不可能
		if (n % i == 0) {
			// 我们枚举到i时，n中就不再包含2~i-1中的任何质因子了，且n % i == 0，因此i也不再有2~i-1中的任何质因子，所以i一定是质数
			int num = 0;
			while (n % i == 0) {
				n /= i;
				num++;
			}
			cout << i << " " << num << endl;
		}
	}
	// 数n最多只存在一个大于sqrt(n)的质因子，除开所有质因子后，若值依然大于1，则此时的n就是最大的质因子
	if (n > 1) {
		cout << n << " " << 1 << endl;
	}
}

时间复杂度最差是$O(\sqrt{n})$，最好是$lo{g}_{2}n$，这里的数n是不断除自己的因子，可以降低时间复杂度

三、筛法求素数

1. 朴素筛法

使用2~n之间的数进行剔除

如果某个数p没有被删除，就意味着我们使用2~p-1没有把p删除，则p一定是质数

// 求1~n中素数的数量
int getPrimes(int n) {
	// 表示数组中的数是否被删除
	vector<bool> isDeleted(n + 1, false);
	int cnt = 0;
	for (int i = 2; i <= n; i++) {
		if (!isDeleted[i]) {
			cnt++;
		}
		// 删除i的倍数
		for (int j = i + i; j <= n; j += i) {
			isDeleted[j] = true;
		}
	}
	return cnt;
}

当i=2时，内层循环执行$n/2$，当i=3时，内层循环执行$n/3$，…，当i=n时，内层循环执行$n/n$，时间复杂度为$\frac{n}{2}+\frac{n}{3}+...+\frac{n}{n}$，调和级数，当n趋近于正无穷时，极限是$n(\ln n+0.577)$，时间复杂度接近于$O(nlo{g}_{2}n)$

2. 埃氏筛法

埃氏筛法改进： 素数的倍数一定不是素数，在用素数剔除时，一定会剔除合数。没必要再用合数剔除，只用素数剔除

由算术基本定理，只需要使用2~n-1中的素数进行剔除即可

// 求1~n中素数的数量
int getPrimes(int n) {
	// 表示数组中的数是否被剔除
	vector<bool> isDeleted(n + 1, false);
	int cnt = 0;
	for (int i = 2; i <= n; i++) {
		if (!isDeleted[i]) {
			cnt++;
			// 删除素数i的倍数
			for (int j = i + i; j <= n; j += i) {
				isDeleted[j] = true;
			}
		}
	}
	return cnt;
}

时间复杂度为$\frac{n}{2}+\frac{n}{3}+...+\frac{n}{n}$，其中分母只有素数，根据素数定理，1~n中大概有$\frac{n}{\ln n}$个素数，时间复杂度大概是朴素解法的$\frac{\ln n}{n}$倍，即$(\ln n{)}^2$，真实的时间复杂度大概是$O(nloglogn)$，基本上就是$O(n)$

3. 线性筛法

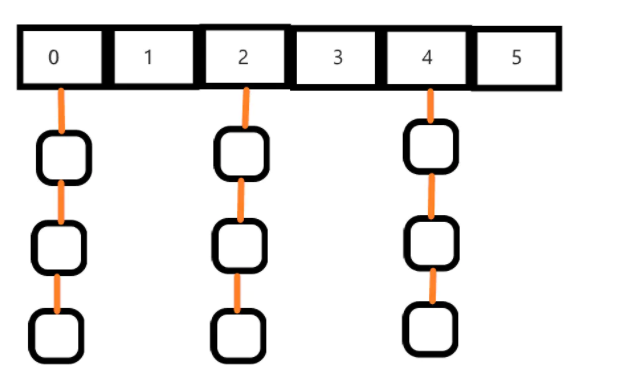
算法核心：一个数n只会被最小的质因子筛掉

int getPrimes(int n) {
	vector<int> primes;                    // 记录素数
	vector<bool> isDeleted(n + 1, false);  // 表示数组中的数是否被删除
	int cnt = 0;
	for (int i = 2; i <= n; i++) {
		if (!isDeleted[i]) {
			primes.push_back(i);           // 没有被筛掉，则记录素数
			cnt++;
		}
		// 开始枚举n的质因子
		int up = n / i;
		for (int j = 0; primes[j] <= up; j++) {
			isDeleted[primes[j] * i] = true; // primes[j]一定是i的最小质因子
			if (i % primes[j] == 0) break;
		}
	}
	return cnt;
}

当i % primes[j] != 0时，说明此时遍历到的primes[j]不是i的质因子，且因为当前的i是素数表里最大的素数，则primes[j] < i，所以primes[j] * i的最小质因子就是primes[j]

当有i % primes[j] == 0时，说明i的最小质因子是primes[j]，因此primes[j] * i的最小质因子也就应该是prime[j]，之后接着用isDeleted[primes[j+1] * i] = true去筛合数时，就不是用最小质因子去更新了，因为i有最小质因子primes[j] < primes[j+1]，此时的primes[j+1]不是primes[j+1] * i的最小质因子，此时就应该退出循环，避免之后重复进行筛选

图中的X都是primes[j]等于对应数的最小质因子是被筛掉的