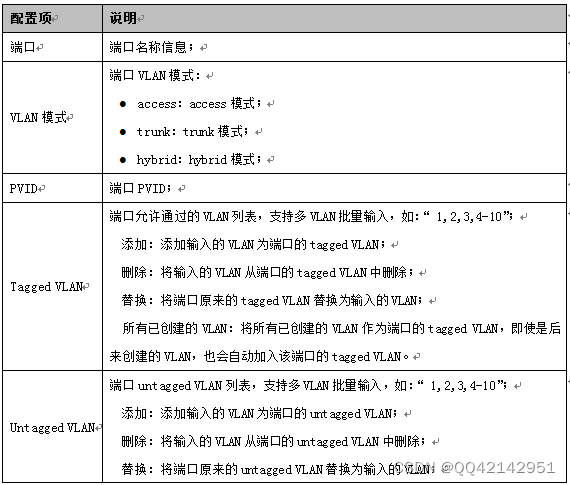
随着zk的兴起,出现了一大批zk友好且面向算术化(Arithmetization-Oriented)的哈希函数,如MiMC-Hash, Rescue–Prime, Poseidon等等,本文要介绍的Anemoi是今年新出的一种zk友好且面向算术化的哈希函数,与其他哈希函数相比,Anemoi具有以下特点:
-
可以被用于Groth16, Plonk等证明系统中
-
包含对特定应用的优化,如merkle tree的证明
-
性能优越,参见下表

1. Flystel Structure
Flystel结构是butterfly和Feistel的结合:butterfly + Feistel = Flystel
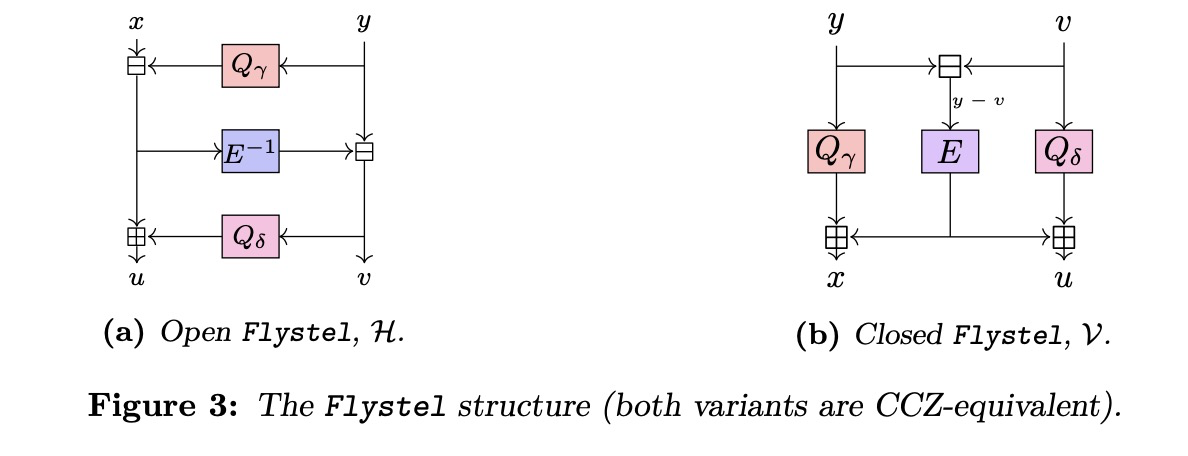
图(a)是开放的Flystel结构,图(b)是封闭的Flystel结构,图(a)通过一次旋转即可得到图(b),这样做的好处是消除了逆运算。
在实际运算中Flystel一般定义在 F q F_q Fq中,并且 Q r ( X ) = β x 2 + γ Q_r(X) = \beta x^2 +\gamma Qr(X)=βx2+γ, Q δ ( X ) = β x 2 + δ Q_{\delta}(X) = \beta x^2 +\delta Qδ(X)=βx2+δ, E ( X ) = X α E(X) = X^{\alpha} E(X)=Xα
所以对于封闭的Flystel结构,我们有下面等式成立
u
=
(
y
−
v
)
α
+
β
v
2
+
δ
x
=
(
y
−
v
)
α
+
β
y
2
+
γ
u = (y-v)^{\alpha} + \beta v^2 + \delta \\ x = (y-v)^{\alpha} + \beta y^2 + \gamma
u=(y−v)α+βv2+δx=(y−v)α+βy2+γ
2. Anemoi
Anemoi每轮主要由 constant addition 、linear layer M和 S-box layer这三步构成:
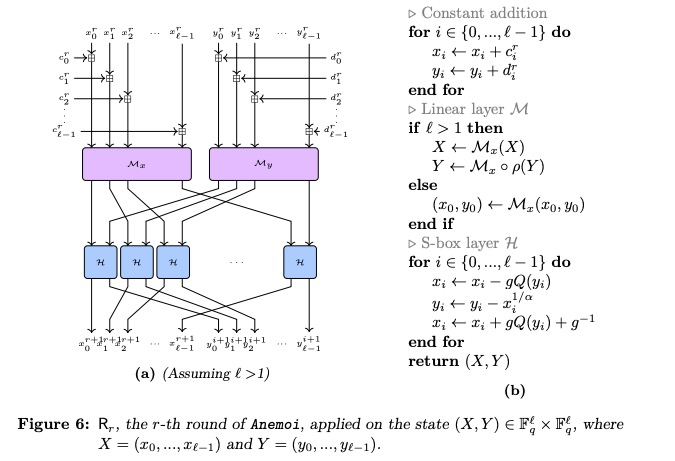
- 如果 l l l很小,那么域则需要很大,一般用于基于配对的证明系统,如groth16,plonk等
- 如果 l l l很大,则域不需要很大,一般用于基于FRI的证明系统
2.1 Diffusion Layer M.
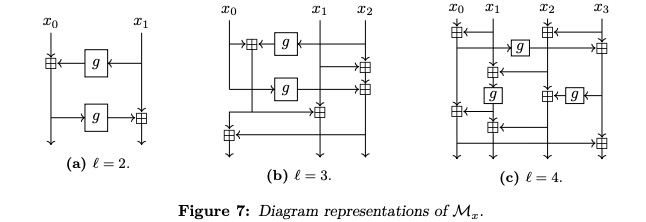
当
l
∈
{
1
,
2
,
3
,
4
}
l \in \{1,2,3,4\}
l∈{1,2,3,4}时,我们可以使用矩阵
M
x
l
M_x^l
Mxl来表达,如
M
x
1
=
M
x
2
=
[
1
g
g
g
2
+
1
]
M_x^1=M_x^2 = \left[ \begin{array}{cc|r} 1 & g\\g & g^2+1 \end{array} \right]
Mx1=Mx2=[1ggg2+1]
输出等于
[
x
0
,
x
1
]
⋅
M
x
2
[x_0,x_1] \cdot M_x^2
[x0,x1]⋅Mx2
2.2 S-box Layer S
令H是Flystel结构,则
S
(
X
,
Y
)
=
(
H
(
x
o
,
y
o
)
,
.
.
.
,
H
(
x
l
−
1
,
y
l
−
1
)
)
S(X,Y) = (H(x_o,y_o),...,H(x_{l-1},y_{l-1}))
S(X,Y)=(H(xo,yo),...,H(xl−1,yl−1))
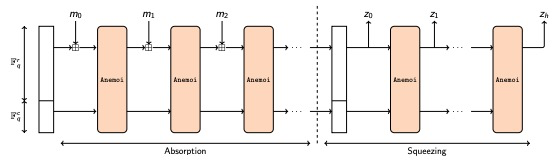
2.3 完整的Anemoi
遵循海绵结构构造
3. R1CS 约束
我们使用封闭的Flystel结构,得到如下S-Box验证等式
(
y
−
v
)
α
+
β
v
2
+
δ
−
u
=
0
(
y
−
v
)
α
+
β
y
2
+
γ
−
x
=
0
(y-v)^{\alpha} + \beta v^2 + \delta -u = 0\\ (y-v)^{\alpha} + \beta y^2 + \gamma -x = 0
(y−v)α+βv2+δ−u=0(y−v)α+βy2+γ−x=0
参考
- https://eprint.iacr.org/2022/840.pdf
- https://github.com/anemoi-hash/anemoi-hash
- https://github.com/FindoraNetwork/noah/blob/develop/crypto/src/basic/anemoi_jive.rs






![[附源码]java毕业设计医院挂号系统](https://img-blog.csdnimg.cn/fe9279c6e07a40e9866f4345c23f4885.png)