题目截图

题目分析

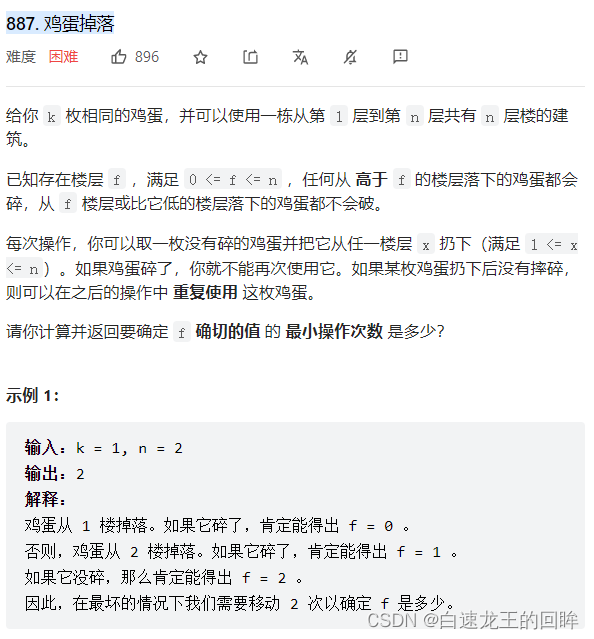
• 变量：鸡蛋的数量，楼层n，尝试的次数m
• 有一个单调性容易发现：尝试的次数越多，能解决楼层越高的确切值
• 另一个单调性：鸡蛋的数量越多，能够解决楼层越高的确切值
• 因此，不妨dp[i][j]表示i个鸡蛋，m次尝试，最多能够解决的楼层数
• 初始：dp[1][1] = 1
• 对于dp[i][j]而言，这次尝试可以分清当前楼层的
• 如果没刷碎，最多可以解决dp[i][j - 1]个楼层
• 如果摔碎了，最多可以解决dp[i - 1][j - 1]个楼层
• 因此dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1] + 1
• why是dp[i - 1][j - 1] + dp[i][j - 1]？这不应该两者取其一吗
• 解答：因为有一个前提，就是一开始必定是二分找的，所以比如我们找x层楼，一开始在x / 2扔一个蛋；不管碎了还是没碎，要么往上要么往下继续扔，虽然说实际上两种情况只能选其一；但是，从理论上分析这两边应该都是需要被覆盖的
• 我们需要找到最小的j，使得dp[k][j] >= n即可

ac code

class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        # dp[i][j]:表示i个鸡蛋，尝试j次能够最多搞定L层楼的f
        # 掉了下去，要么碎要么不碎
        # 碎了：dp[i - 1][j - 1]
        # 不碎: dp[i][j - 1]
        # 掉的那层: 1
        # dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1] + 1
        # 最小的j，s.t. dp[k][j] >= n
        # dp[1][1] = 1
        # 最多n次
        dp = [[0] * (n + 1) for _ in range(k + 1)]
        dp[1][1] = 1
        for i in range(1, k + 1):
            for j in range(1, n + 1):
                dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1] + 1
                if i == k and dp[i][j] >= n:
                    return j
        return n

总结

• 关键就是dp的定义
• 万物皆可dp