一、前序遍历 | 根左右(DLR)
1.1 简介
前序遍历简介也叫先序遍历
前序遍历 可以分为三部分:根、左子树、右子树
先遍历根节点 、再遍历左子树、再遍历右子树
左/右 子树遍历方法:先访问根节点,再访问 左孩子节点,访问到左孩子节点之后判断该左孩子节点是否是 叶子节点(叶子节点 也就是说 这个节点下没有任何节点,形容的还是很贴切的,因为一棵树的最末端的部分就是叶子) 如果不是叶子节点,继续按照 根左右 的访问顺序继续访问,当访问到该左孩子是叶子节点 时,再访问 右孩子 节点,同理 也按照 根左右 的顺序进行访问 右孩子节点,同理和左孩子一样 判断该节点是否是 叶子节点,不是叶子节点 继续 按照 根左右 的遍历顺序进行访问,直到访问到整棵树的 最后一个 叶子节点的 右孩子 表示 该左子树/右子树遍历结束
1.2 示例
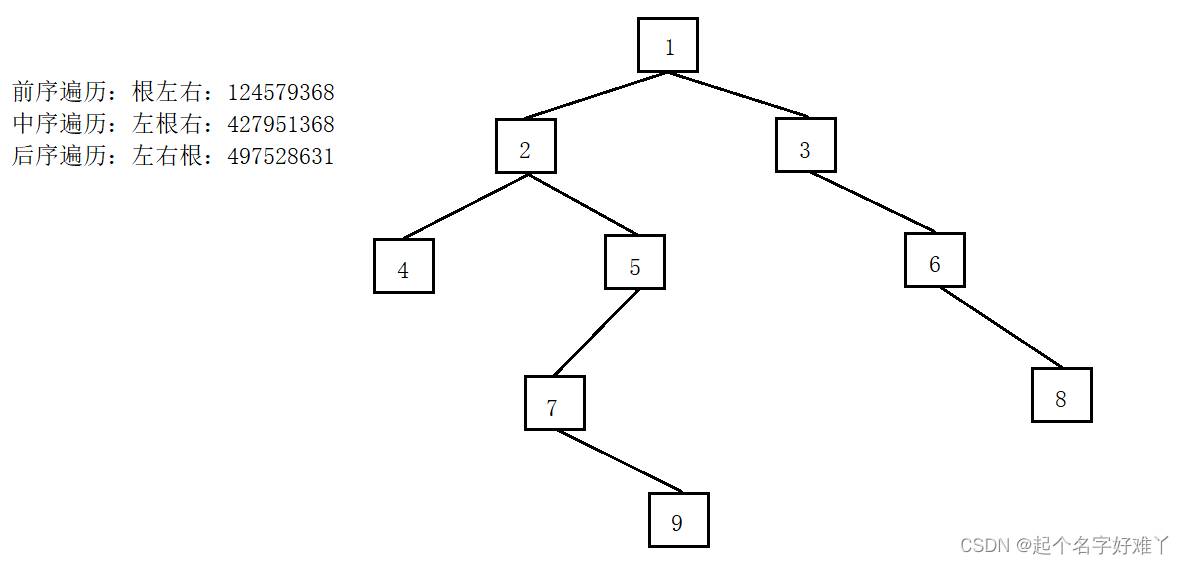
例如上图:
左子树:
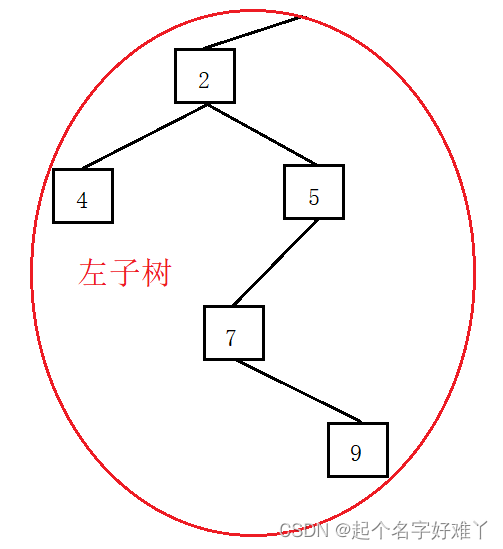
1.2.1
访问 根节点 1 ,节点 1 为 根节点 因此 先访问 节点 1,且接下俩访问 节点 1 的左孩子
1.2.2
访问 节点 2,节点 2 为 节点1 的左孩子,且 节点 2 为根节点,因此 现在 访问 节点 2,接下来继续访问 节点 2 的左孩子
1.2.3
访问 节点 4,节点 4 为 节点 2 的左孩子,且 节点 4 为根节点,因此 现在遍历 节点 4,且接下来 继续访问 节点 4 的左孩子
1.2.4
访问 节点 5 ,节点 4 没有左孩子与右孩子,因此 节点 4 为叶子节点,表示 根节点 2 的 左子树已经遍历结束,因此访问 节点 2 的 右孩子 节点 5,且 节点 5 为非叶子节点,接下来 继续访问 节点 5 的 左孩子
1.2.5
访问 节点 7 ,节点 7 为 节点 5 的左孩子,且节点 7 为非叶子节点,接下来 继续访问 节点 7 的左孩子节点
1.2.6
访问 节点 9 ,根节点 7 没有左孩子 因此访问 节点 7 的右孩子 节点 9 ,且节点 9 为叶子节点,因此表示 根节点 1 的 左子树 已经全部遍历结束,接下来 遍历 根节点 1 的右子树
右子树:
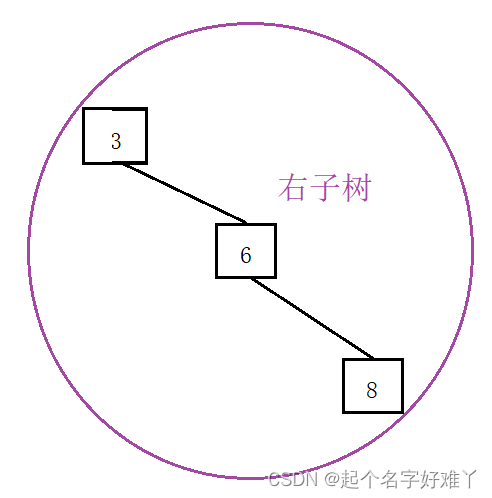
1.2.7
访问 节点 3 ,遍历右子树 先访问 根节点 1 的 右孩子 节点 3,节点 3 为非叶子节点 继续 访问 左孩子,节点 3 没有 左孩子 因此 访问 节点 3
1.2.8
访问 节点 6,节点 3 为非叶子节点,因此访问 该节点的 左孩子,由于没有左孩子 ,因此 访问右孩子 节点 6,节点 6 为非叶子节点,且为根节点,继续访问 节点 6 的 左孩子节点
1.2.9
访问 节点 8 ,节点 6 没有左孩子,因此访问 节点 6 的右孩子 节点 8,且节点 8 为叶子节点,表示整棵树的遍历结束
前序遍历 顺序为: 1 -> 2 -> 4 -> 5 -> 7 -> 9 -> 3 -> 6 -> 8
前序遍历基本性质:
- 遍历顺序为 先根再左再右
- 遍历结束标志,遍历右子树的最后一个子树的右孩子为叶子节点,或右孩子节点为空(即不存在)则表示遍历结束
- 最先遍历根节点,遍历顺序的第一个即 为整棵树的根节点
二、中序遍历 | 左根右(LDR)
2.1 简介
前序遍历 可以分为三部分:左子树、根、右子树
先遍历左子树 、再遍历根节点、再遍历右子树
中序遍历顺序:先访问该树的左子树 , 再访问该树的根节点,最后访问该树的右子树
中序遍历方法:先访问一棵树的左孩子节点,若该节点为非叶子节点,继续访问该节点的左孩子,直到遍历到叶子节点或左孩子节点不存在时,访问右孩子节点,同理并判断该右孩子节点是否是叶子节点或是否存在,若存在且为非叶子节点,那么将继续按照 左根右 访问顺序 遍历,最后遇到叶子节点或 右孩子节点不存在时,访问根节点。
2.2 示例
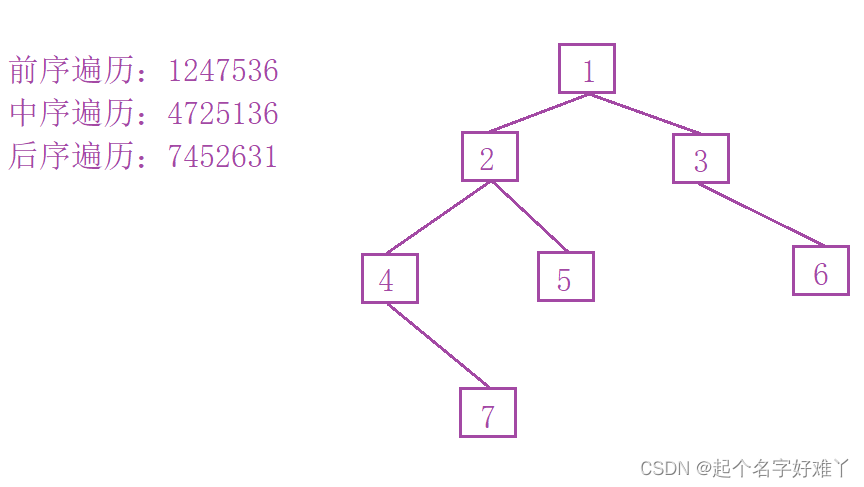
2.2.1
访问 节点 4,首先访问根节点 1 的 左孩子节点 2 ,节点2 为非叶子节点,则继续访问 节点 2 的 左孩子 节点 4 ,节点 4 为 非叶子节点 因此 继续访问 节点 4 的 左孩子 ,节点 4 没有 左孩子 ,因此 接下来 访问 根节点 4 ,因此 节点 4 为第一个访问的 节点,接下来 继续按照 左根右 的顺序 遍历 节点 4 的右孩子 节点。
2.2.2
访问 节点 7,按照 左根右 的 遍历顺序 ,遍历 右孩子:节点 7
2.2.3
访问 节点 2 , 节点 7 为叶子节点,则表示
这一棵子树已经全部遍历结束了,也表示 节点 2 的左子树已经遍历完了 ,因此按照 左根右 的遍历顺序,现在访问 根节点 2
2.2.4
访问 节点 5,访问完 节点 2 之后开始 访问 右孩子 节点 5
2.2.5
访问 根节点 1,节点 5 为叶子节点,因此 表示 根节点 1 的左子树已经全部访问完成,因此 按照 左根右 的遍历顺序,现在 访问根节点 1
2.2.6
访问 节点 3 , 左子树和根节点已经全部访问完成,接下来开始访问 右子树,右子树 第一个为 节点3 的 左孩子节点,由于 节点 3 没有 左孩子,因此现在 访问 根节点 3
2.2.7
访问 节点 6,根节点 3 访问之后 开始访问 右孩子节点 ,即 节点 6,且 节点 6 为叶子节点,因此表示 整个遍历 结束。
中序遍历 顺序为: 4 -> 7 -> 2 -> 5 -> 1 -> 3 -> 6
中序遍历基本性质:
- 遍历顺序为 先左子树再根节点最后右子树
- 根据根节点可以把中序遍历的顺序划分为 左子树与右子树
三、后序遍历 | 左右根(LRD)
3.1 简介
熟悉过以上两种之后,应该也熟悉了这个套路
无非还是分为以下三大部分
左子树、右子树、根
后序遍历为 左右根 ,因此 遍历的大致顺序为:
先遍历左子树、再遍历右子树、最后遍历 根节点
后序遍历:和前序中序其实都一样,按照 对应顺序访问,如果不是叶子节点就一直 按照遍历的顺序继续访问下去,直到左子树遍历结束,接下来按照同样的方法遍历右子树,右子树遍历结束之后,遍历根节点 因此,整棵树的根节点是 最后一个访问的 ,与前序遍历 恰好相反,前序遍历第一个访问的是根节点
3.2 示例
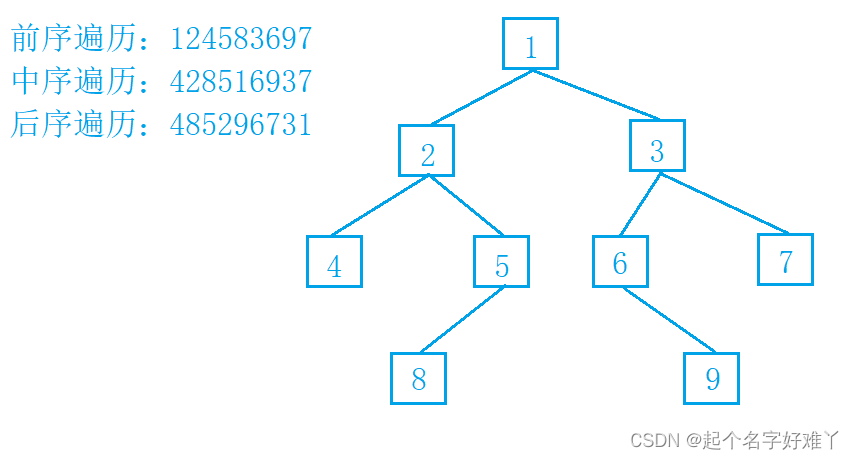
先遍历 根节点 1 的 左子树
3.2.1
访问节点 4 , 按照左右根 访问顺序,首先访问 根节点 1 的左孩子 节点 2,节点 2 为非叶子节点,继续访问 节点 2 的左孩子节点 4,节点 4 为叶子节点,因此遍历的第一个节点为 节点 4.
3.2.2
访问节点 8,节点 2 的左孩子节点已经访问结束,接下来 继续访问 节点 2 的右孩子 节点 5 节点 5 为非叶子节点 因此继续访问 节点 5 的 左孩子 节点 8,且节点 8 为叶子节点
3.2.3
**访问节点 5 **,因为 节点 8 为叶子节点 因此 节点 5 的左子树已经全部访问完成,接下来 按照 左右根的顺序,继续访问节点 5 的右孩子,因为 节点 5 没有右孩子,因此现在访问 根节点 5
3.2.4
访问节点 2 , 节点 5 访问完之后,表示 节点 2 的左右子树已经全部访问完毕,因此按照 左右根,现在 访问 根节点 2
节点 1 的左子树已经全部遍历结束,因此接下里开始遍历,右子树
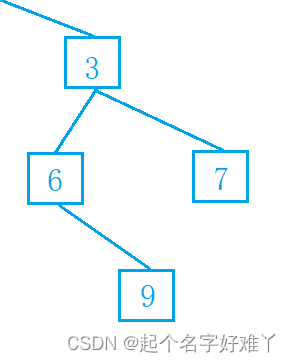
3.2.5
访问节点 9,首先访问 节点 3 节点 3 为 非叶子节点,因此继续 访问 节点 3 的左孩子 节点 6,节点 6 同样为 非叶子节点,因此继续访问 节点 6 的左孩子,节点 6 没有左孩子,因此 访问 节点 6 的右孩子节点 9,且节点 9 为叶子节点
3.2.6
访问节点 6,节点 9 为叶子节点,表示 根节点 6 的 左右子树已经全部遍历结束,因此按照 左右根的 顺序,接下来 访问根节点 6.
3.2.7
访问节点 7,节点 6 遍历完之后表示 节点 3 的左子树已经全部遍历结束,接下来开始遍历 节点 3 的右子树 中的 节点 7,且 节点 7 为叶子节点,因此 节点 3 的右子树也全部遍历结束
3.2.8
访问节点 3,节点 3 的左右子树已经全部遍历结束,按照 左右根 的遍历顺序,因此 现在访问 根节点 3,也表示 根节点 1 的左右子树 也已经全部 访问结束,接下俩 访问 根节点 1
遍历根节点
3.2.9
访问根节点 1,根节点 1 的左右子树全部遍历结束之后,最后遍历整棵树的根节点 1,也表示整棵树遍历结束。
后序遍历 顺序为:4 -> 8 -> 5 -> 2 -> 9 -> 6 -> 7 -> 3 -> 1
后序遍历基本性质:
- 后序遍历顺序为 先左子树再右子树最后根节点
- 后序遍历顺序中的最后一个节点为根节点