前提

1. 时间复杂度：

2. 约化(Reducibility)

• 如果能找到一个变化法则，对任意一个A程序的输入，都能按照这个法则变换成B程序的输入，使两程序的输出相同，那么我们说，问题A可以约化为问题B。
• 一个问题A可以约化为问题B的含义是，可以用问题B的解法解决问题A。（也可以简单理解，问题A是B的一种特殊情况。）
• 例如求解一元一次方程这个问题可以约化为求解一元二次方程，即可以令对应项系数不变，二次项的系数为0，将A的问题的输入参数带入到B问题的求解程序去求解。
• 约化还具有传递性，A可以化约为B，B可以约化为C，那么A也可以约化为C

P问题

• 可以在多项式时间内，解决的问题
• 复杂度在以下区间内：
  
• 该算法的时间复杂度是多项式级的，比如n个数中间找到最大值，或者n个数排序。

NP问题

• 可以在多项式时间内，验证一个解的问题
• (Non-deterministic Polynomial非确定性多项式问题)
• 理解：
• 不知道这个问题存不存在一个多项式时间的算法，所以叫非确定性（non-deterministic），但是我们可以在多项式时间内验证并得出这个问题的一个正确解。举例：

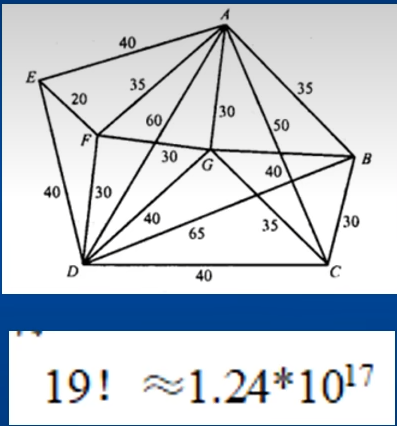
著名NP类问题：旅行家推销问题(TSP)。即有一个推销员，要到n个城市推销商品，他要找出一个包含所有n个城市的环路，这个环路路径小于a。我们知道这个问题如果单纯的用枚举法来列举的话会有(n-1)! 种，已经不是多项式时间的算法了，(注：阶乘算法比多项式的复杂)。
那怎么办呢？我们可以用猜的，假设人品爆炸猜几次就猜中了一条小于长度a的路径，TSP问题解决了，皆大欢喜。可是，我不可能每次都猜的那么准，也许我要猜完所有种方案呢？
所以我们说，这是一个NP类问题。也就是，我们能在多项式的时间内验证并得出问题的正确解，可是我们却不知道该问题是否存在一个多项式时间的算法，每次都能解决他(注意，这里是不知道，不是不存在)。

所以这就引出了这类讨论的一个千年问题：是否 NP类问题=P类问题？

即，是否所有能在多项式时间内验证得出正确解的问题，都是具有多项式时间算法的问题呢？

太让人震惊了，要是解决了这个问题，那岂不是所有的NP问题都可以通过计算机来解决？

为了证明这个千古难题，科学家想出了很多办法。其中之一就是问题的约化。所谓问题约化就是，可以用问题B的算法来解决A ，我们就说问题A可以约化成问题B。约化是具有传递性的，如A约化到B，B约化到C，A就可以约化到C，同时不断约化下去，我们会发现一个很惊人的特性，就是他一定会存在一个最大的问题，而我们只需要解决了这个问题，那其下的所有问题也就解决啦！这就是我们所说的NPC问题的概念

引到NP问题里就是，对于同一类的所有的NP类问题，若他们都可以在多项式时间内约化成最难的一个NP类问题，（我们直观的认为，被约化成的问题应具有比前一个问题更复杂的时间复杂度）当我们针对这个时间复杂度最高的超级NP问题要是能找到他的多项式时间算法的话，那就等于变向的证明了其下的所有问题都是存在多项式算法的，即NP=P！！！！给出NPC问题定义。

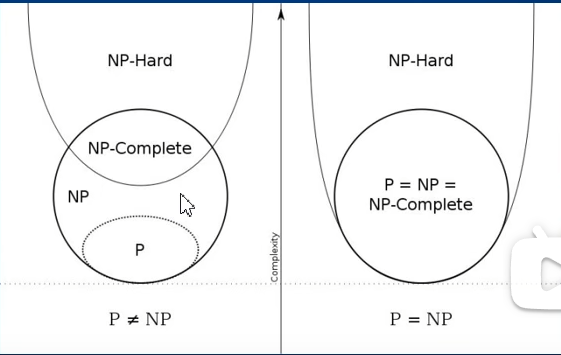
（1）左图

• P一定属于NP
  多项式时间内解决，那多项式时间内一定能验证
• NP-Complete一定是NP
• 是NP的NP-Hard是NP-Complete，也有不是NP的NP-Hard

（2）右图

• P一定是NP
  多项式时间内解决，那多项式时间内一定能验证
• NP-Complete一定是NP
• 是NP的NP-Hard是NP-Complete

NPHard问题

• 所有NP问题都能多项式时间内归约（可理解为转化）到X（复杂度大于等于原NP问题）问题，X是NP-Hard问题
• 所有的NP问题都能约化到它，但是它不一定是一个NP问题

NP-Complete问题

• 所有NP问题都能多项式时间内归约（可理解为转化）到X（复杂度大于等于原NP问题）问题，且X是NP问题，X是NP-Complete问题

• 定义要满足2个条件： 它得是一个NP问题；所有的NP问题都可以约化到它

• 证明npc问题思路： 先证明它至少是一个NP问题，再证明其中一个已知的NPC问题能约化到它

• 常见的NP-Complete问题：
  逻辑电路，Hamilton问题、旅行商问题
  

其它：

• P一定是NP
  多项式时间内解决，那多项式时间内一定能验证
• NP是否为P未解决

https://www.bilibili.com/video/BV1Wz4y1d7wb/?spm_id_from=333.337.search-card.all.click
https://zhuanlan.zhihu.com/p/73953567
https://zhuanlan.zhihu.com/p/99515528