一.将二叉搜索树变成有序链表

二.从前序遍历和中序遍历构建二叉树

三.从中序遍历和后续遍历创建字符串

四.二叉树创立字符串

五.订正题目

六.排序子序列

七.二叉树非递归遍历

1.前序遍历

3.后续遍历

一.将二叉搜索树变成有序链表

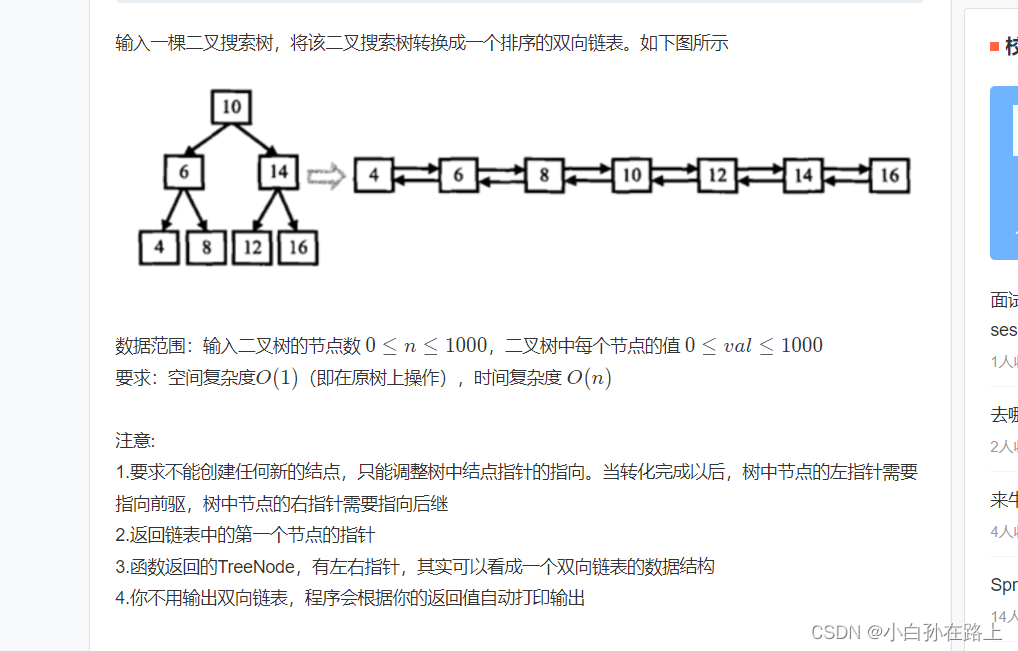
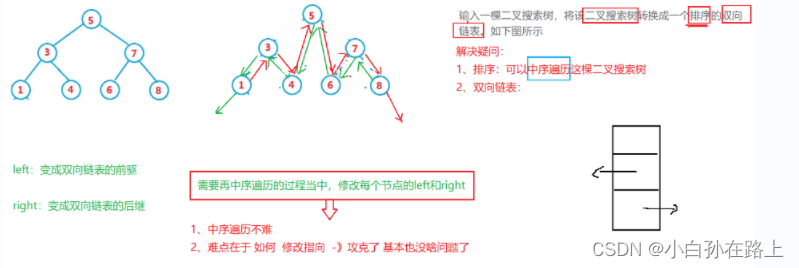
我们的思路就是因为一颗二叉搜索树所以中序遍历是有序的,从小到大排的.

所以我们的思路就是一边遍历一边修改节点指向.因为是双向链表,就把left和right修改指向

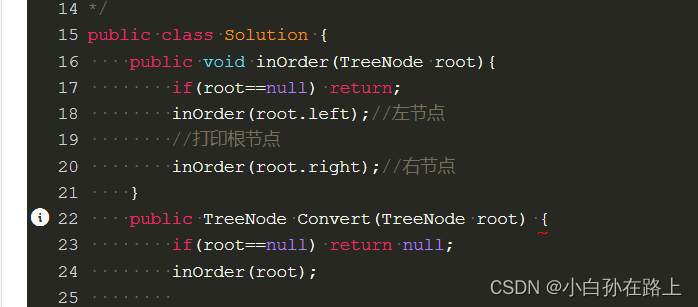
所以再需要打印那一步我们开始搞事情,我们需要对他修改指向,根据上图所示,我们最好就是

left改为下一个的.right改为上一个的.

我们就从第一个走到根节点这一步开始思考

如果是第一个那么就是左子树最左边的树,那么他的下一个就是null.上一个就是他的根节点.

然后回推到他的下一个,他的下一个就是刚刚那个节点,上一个就是他的右子树.

所以我们需要有一颗后继节点.记录上一个节点的位置.

并且这个节点得是成员变量.不然每次递归,他都会重置

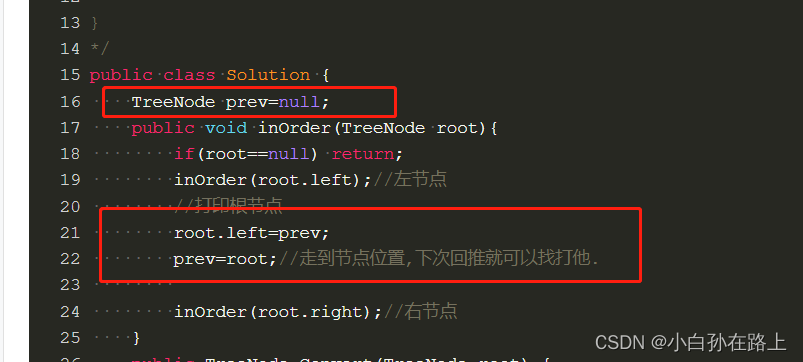
这里我们发现,root指向了prev.但是prev并没有连接到root.其实prev的right就是root啊

所以我们需要在他移向root之前让他指向cur;

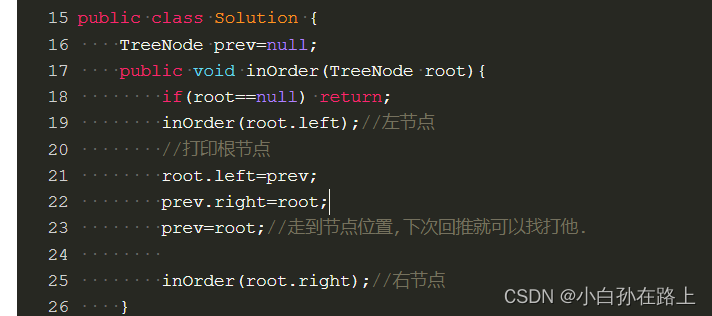
根据如此递归,递归完成的时候,就变成了双向链表,就到最后一个节点的时候,因为prev还是和他连接的,他的左节点连接的是prev.他的右节点本来就是null.所以没毛病

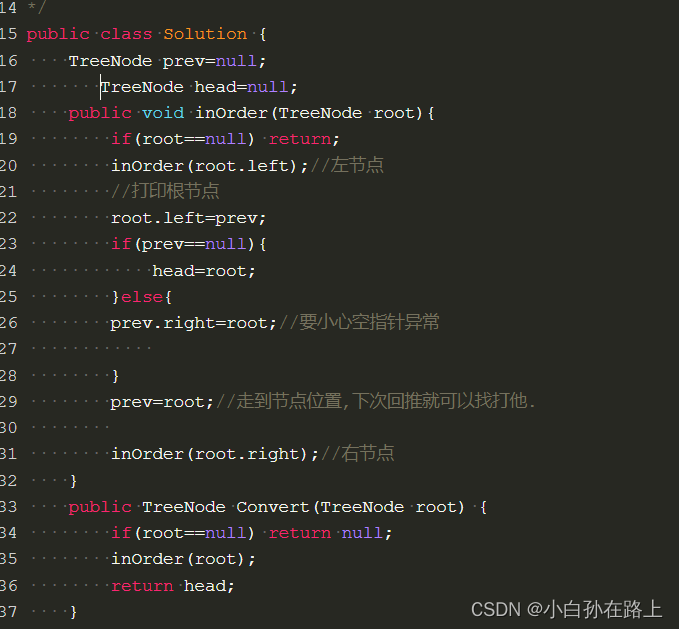
那就回到了主函数,

我们现在虽然得到的是主函数,但是root还是指向的是左节点,我们需要一个头结点

就开始迭代找.或者定义一个头结点,当prev为null的时候满足

方法一：非递归版
解题思路：
1.核心是中序遍历的非递归算法。
2.修改当前遍历节点与前一遍历节点的指针指向。
    import java.util.Stack;
    public TreeNode ConvertBSTToBiList(TreeNode root) {
    if(root==null)
    return null;
    Stack<TreeNode> stack = new Stack<TreeNode>();
    TreeNode p = root;
    TreeNode pre = null;// 用于保存中序遍历序列的上一节点
    boolean isFirst = true;
    while(p!=null||!stack.isEmpty()){
    while(p!=null){
    stack.push(p);
    p = p.left;
    }
    p = stack.pop();
    if(isFirst){
    root = p;// 将中序遍历序列中的第一个节点记为root
    pre = root;
    isFirst = false;
    }else{
    pre.right = p;
    p.left = pre;
    pre = p;
    }
    p = p.right;
    }
    return root;
    }
方法二：递归版
解题思路：
1.将左子树构造成双链表，并返回链表头节点。
2.定位至左子树双链表最后一个节点。
3.如果左子树链表不为空的话，将当前root追加到左子树链表。
4.将右子树构造成双链表，并返回链表头节点。
5.如果右子树链表不为空的话，将该链表追加到root节点之后。
6.根据左子树链表是否为空确定返回的节点。
    public TreeNode Convert(TreeNode root) {
    if(root==null)
    return null;
    if(root.left==null&&root.right==null)
    return root;
    // 1.将左子树构造成双链表，并返回链表头节点
    TreeNode left = Convert(root.left);
    TreeNode p = left;
    // 2.定位至左子树双链表最后一个节点
    while(p!=null&&p.right!=null){
    p = p.right;
    }
    // 3.如果左子树链表不为空的话，将当前root追加到左子树链表
    if(left!=null){
    p.right = root;
    root.left = p;
    }
    // 4.将右子树构造成双链表，并返回链表头节点
    TreeNode right = Convert(root.right);
    // 5.如果右子树链表不为空的话，将该链表追加到root节点之后
    if(right!=null){
    right.left = root;
    root.right = right;
    }
return left!=null?left:root;        
    }
方法三：改进递归版
解题思路：
思路与方法二中的递归版一致，仅对第2点中的定位作了修改，新增一个全局变量记录左子树的最后一个节点。
    // 记录子树链表的最后一个节点，终结点只可能为只含左子树的非叶节点与叶节点
    protected TreeNode leftLast = null;
    public TreeNode Convert(TreeNode root) {
    if(root==null)
    return null;
    if(root.left==null&&root.right==null){
    leftLast = root;// 最后的一个节点可能为最右侧的叶节点
    return root;
    }
    // 1.将左子树构造成双链表，并返回链表头节点
    TreeNode left = Convert(root.left);
    // 3.如果左子树链表不为空的话，将当前root追加到左子树链表
    if(left!=null){
    leftLast.right = root;
    root.left = leftLast;
    }
    leftLast = root;// 当根节点只含左子树时，则该根节点为最后一个节点
    // 4.将右子树构造成双链表，并返回链表头节点
    TreeNode right = Convert(root.right);
    // 5.如果右子树链表不为空的话，将该链表追加到root节点之后
    if(right!=null){
    right.left = root;
    root.right = right;
    }
return left!=null?left:root;        
    }

二.从前序遍历和中序遍历构建二叉树

因为前序遍历是先根遍历,可以通过前序找到根节点,然后在中序遍历这里找到左子树和右子树

再再左子树和右子树分别找前序遍历的根,如此递归,

但是会发现,每次递归左子树和右子树对应的数组会变小,这里我认为也不需要分隔数组,就只要改变数组指向就好

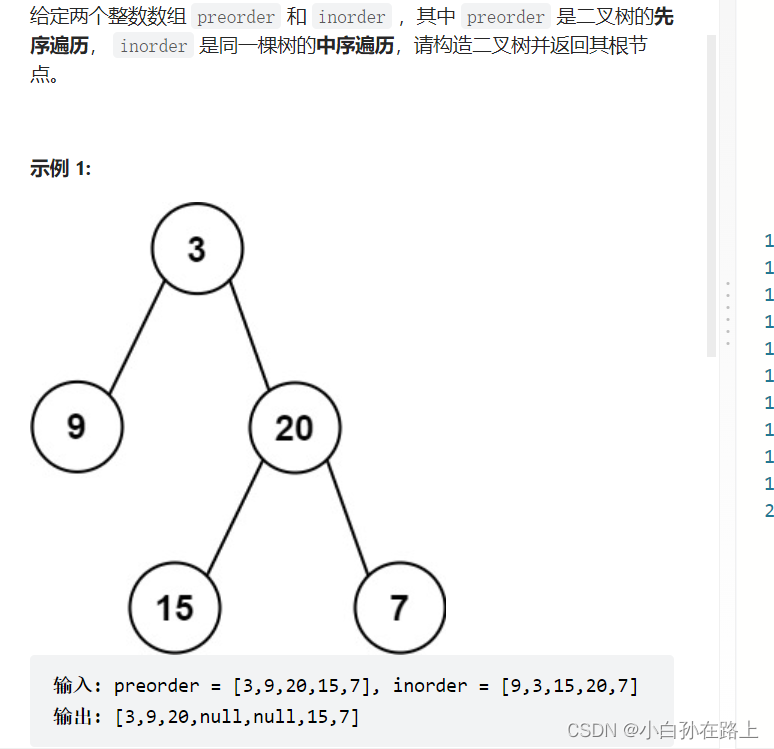
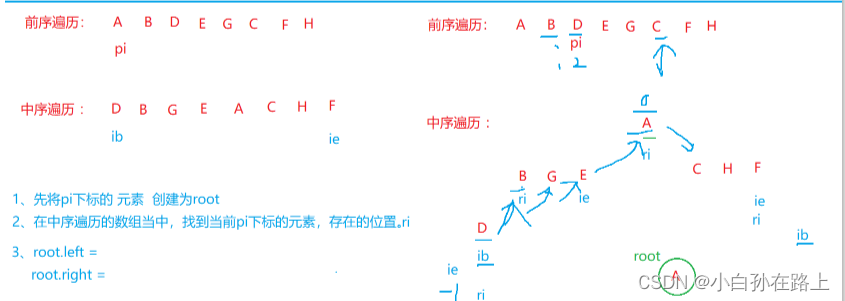
第一步,在前序数组开始遍历,没遍历一个元素,就去中序遍历循环找对应的元素下标

第二步开始分隔中序数组,左边的是左子树右边的是右子树,

定义两个指针来指向左子树和右子树开头和结尾.

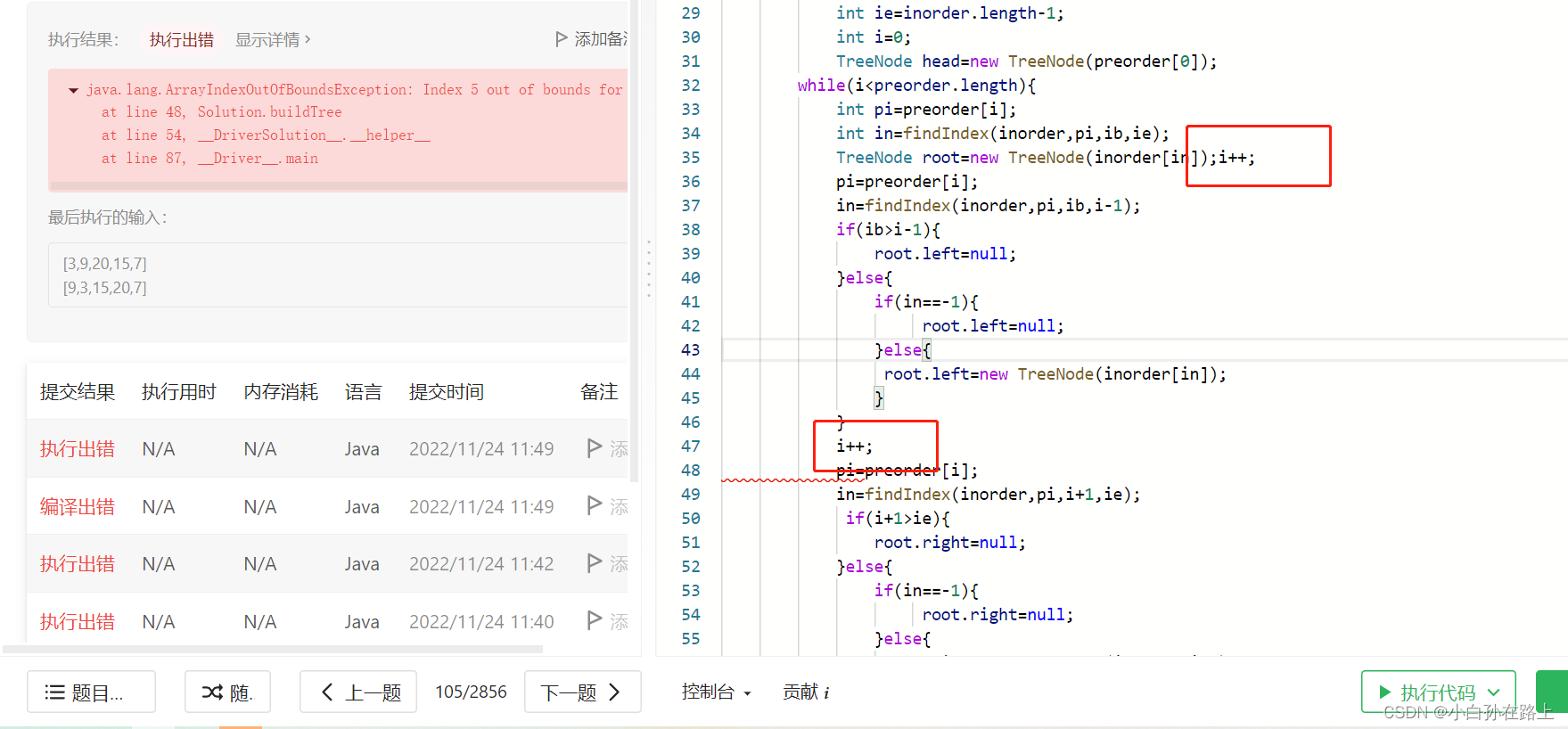
我这里用迭代的方式做,出现了问题一组循环,多组加,就导致可能数组越界

所以应该还是得试试递归的方式

因为考虑到题干中给的函数只有两个数组变量.所以我们另外再建立一个方法,添加指针变量

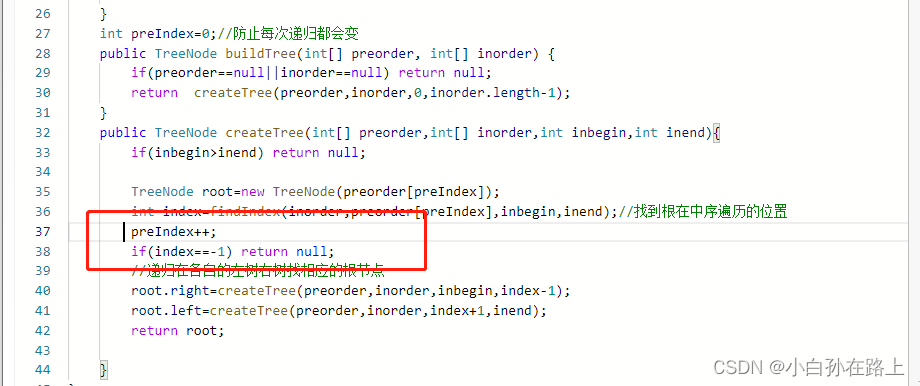
这里我没有考虑完全.如果是到了空节点,就直接递归回去了.就不需要在前序数组再往前一位,

要先判断

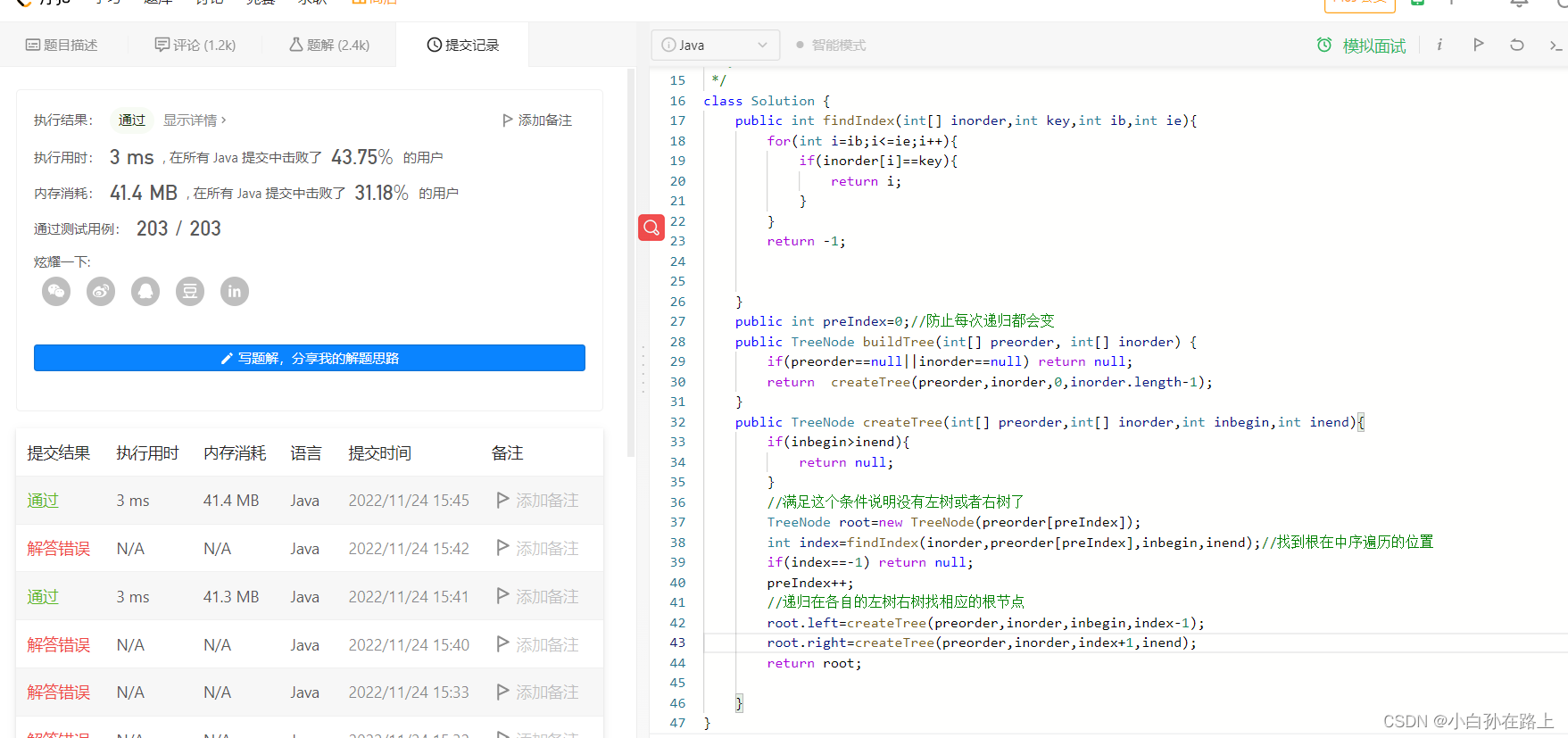
我这里出现了一个及其离谱的错误,左右树创建的时候写反了

这里的思路就是先判断左指针是否大于右指针.

因为每次递归都会找每颗子树自己的根.就会导致指针越来越接近

直到小于或者大于,就说明

已经递归到自身已经不能再往下了,就说明到了null了,所以要给递归弄一个结束条件,也就是这个条件

然后创建每次递归找到的根节点,就以前序遍历为主

再从中序遍历找到对应的下标,把中序数组以下标为界限左右各分为左子树右子树,

再对这次递归的节点的左节点和右节点分别来创建再次进行递归

因为这次递归的节点的左子树的节点又是一个新的根节点,所以就缩小范围按之前数组的界限

就好

class Solution {
    public int findIndex(int[] inorder,int key,int ib,int ie){
        for(int i=ib;i<=ie;i++){
            if(inorder[i]==key){
                return i;
            }
        }
        return -1;


    }
    public int preIndex=0;//防止每次递归都会变
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder==null||inorder==null) return null;
        return  createTree(preorder,inorder,0,inorder.length-1);
    }
    public TreeNode createTree(int[] preorder,int[] inorder,int inbegin,int inend){
        if(inbegin>inend){
            return null;
        }
        //满足这个条件说明没有左树或者右树了
        TreeNode root=new TreeNode(preorder[preIndex]);
        int index=findIndex(inorder,preorder[preIndex],inbegin,inend);//找到根在中序遍历的位置
        if(index==-1) return null;
        preIndex++;
        //递归在各自的左树右树找相应的根节点
        root.left=createTree(preorder,inorder,inbegin,index-1);
        root.right=createTree(preorder,inorder,index+1,inend);
        return root;

    }
}

三.从中序遍历和后续遍历创建字符串

原理跟上题一样,唯一要改变的就是从后往前遍历,

这里发现因为要从后往前遍历,就要把遍历的指针初始为前序数组末尾,

但是不能放在外面因为数组定义在方法外

这里我们的处理方法,就是还是在外面初始化,然后再函数内设为数组末尾就好了

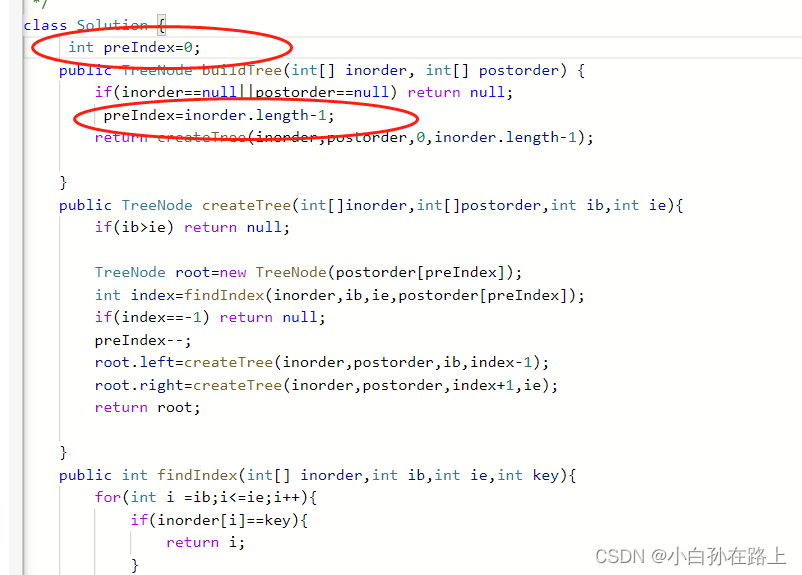
但是还是要注意.因为后续遍历,是左右根.如果从后往前看,就是根右子树,左子树,所以应该是先建立右子树再建立左子树.

class Solution {
     int preIndex=0;
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(inorder==null||postorder==null) return null;
         preIndex=postorder.length-1;
        return createTree(inorder,postorder,0,inorder.length-1); 

    }
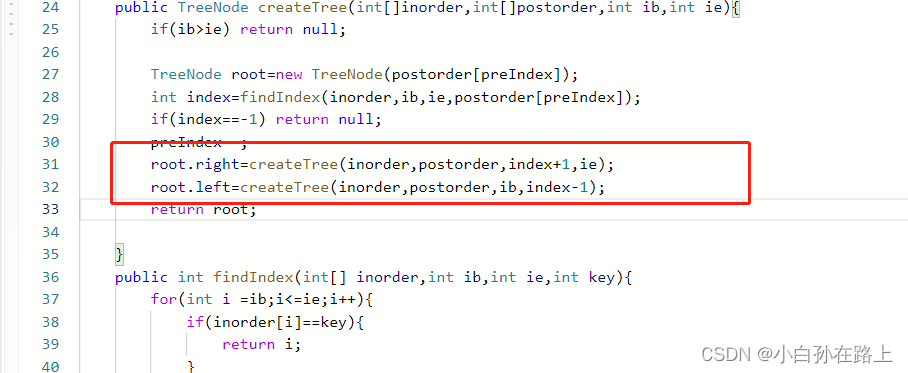
    public TreeNode createTree(int[]inorder,int[]postorder,int ib,int ie){
        if(ib>ie) return null;

        TreeNode root=new TreeNode(postorder[preIndex]);
        int index=findIndex(inorder,ib,ie,postorder[preIndex]);
        if(index==-1) return null;
        preIndex--;
        root.right=createTree(inorder,postorder,index+1,ie);
        root.left=createTree(inorder,postorder,ib,index-1);
        return root;

    }
    public int findIndex(int[] inorder,int ib,int ie,int key){
        for(int i =ib;i<=ie;i++){
            if(inorder[i]==key){
                return i;
            }
        }
        return -1;
    }
}

四.二叉树创立字符串

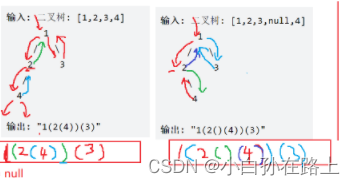
这题很简单,从根开始,遇到左子树开始加个左括号,加上左子树的根,再往下遍历,一个根左右子树遍历完加一个括号,再开始遍历右子树

这里还有一个注意点,如果左子树不是空,但是右子树是空,是不加括号的,

但是如果左子树是空,右子树不是空就加括号.

这里我们重新建立一个方法.因为题目要求string.但是这题涉及到拼接,所以我们在另外一个方法用sb拼接完了,再回到函数tostring就可以

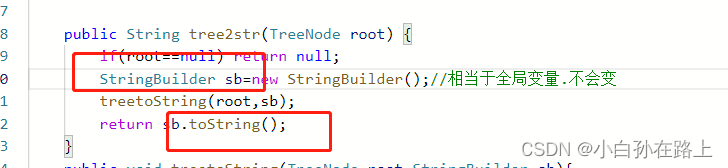
class Solution {
    
    public String tree2str(TreeNode root) {
        if(root==null) return null;
        StringBuilder sb=new StringBuilder();//相当于全局变量.不会变
        treetoString(root,sb);
        return sb.toString();
    }
    public void treetoString(TreeNode root,StringBuilder sb){
        if(root==null) return;
        sb.append(root.val);//不管是根节点还是之后的都可以直接加,因为之后的再地柜之前已经加上了括号

        if(root.left!=null){
            sb.append('(');
            treetoString(root.left,sb);
            sb.append(')');
        }else{
            if(root.right==null){
                return;//左节点为空右节点为空的情况不用考虑
            }else{
                sb.append("()");//左节点为空,右节点为空,根据题意需要加上括号
            }
        }
        if(root.right==null){
            //这种情况就是左节点为null.且右节点也为null的 情况
            return;
        }else{
            //这种情况就是左节点不为null,且右节点也不为null的情况
             sb.append('(');
            treetoString(root.right,sb);
            sb.append(')');
        }

五.订正题目

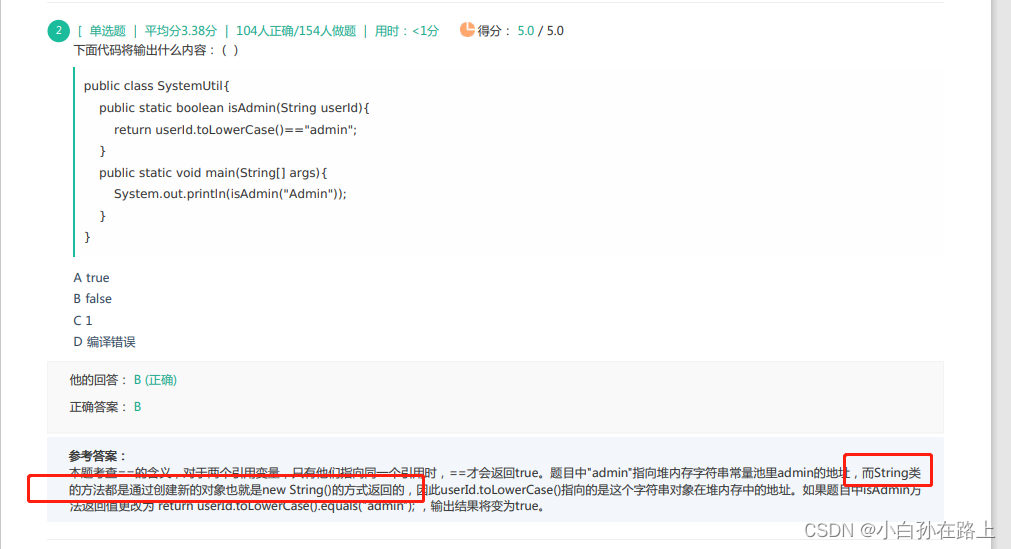
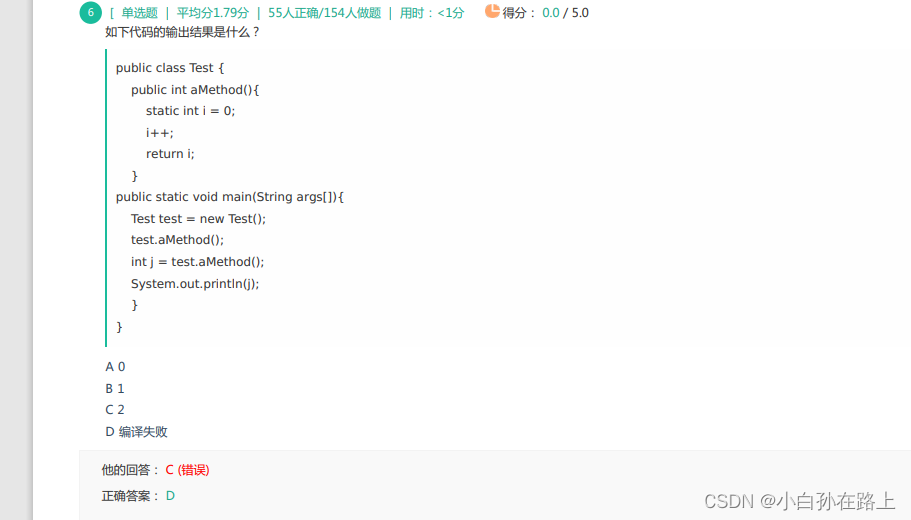
普通方法里不能有静态变量.静态方法也不能有静态变量,静态修饰的属于类变量,

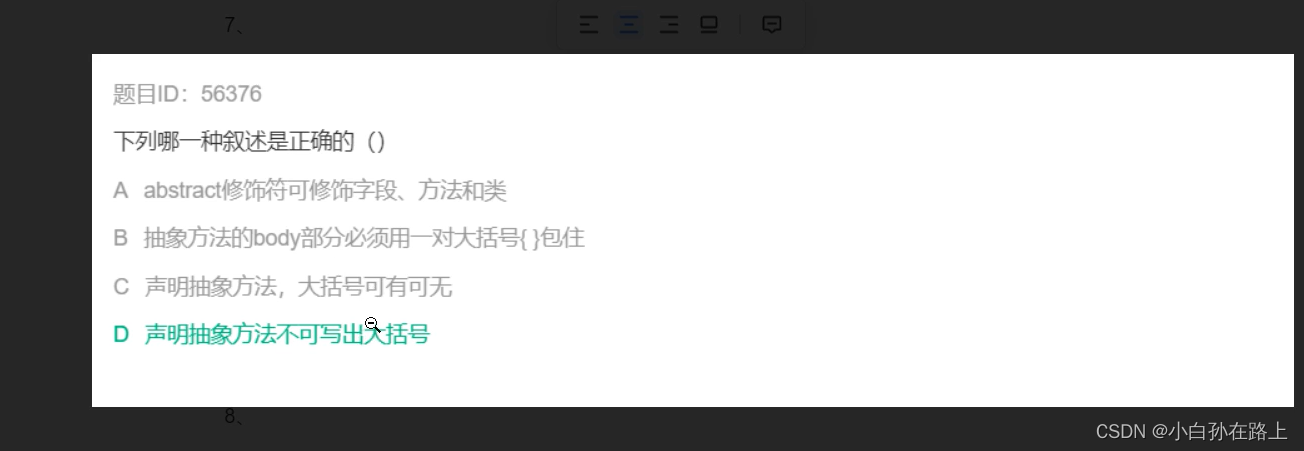
abstract不能修饰字段

对成员变量的赋值必须放在方法的内部

六.排序子序列

非递增就是递减但是有连续相同的元素或者只有递减

所以这道题我们的思路就是先接收

然后判断,是否一直递减就为一组,有相同的,就继续往后加

import java.util.*;
public class Main{
    public static void main(String[] args){
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        int[] array=new int[n+1];
        for(int i=0;i<n;i++){
            array[i]=sc.nextInt();
        }//所有数据接收完整开始判断
        int  count=0;
        int i=0;
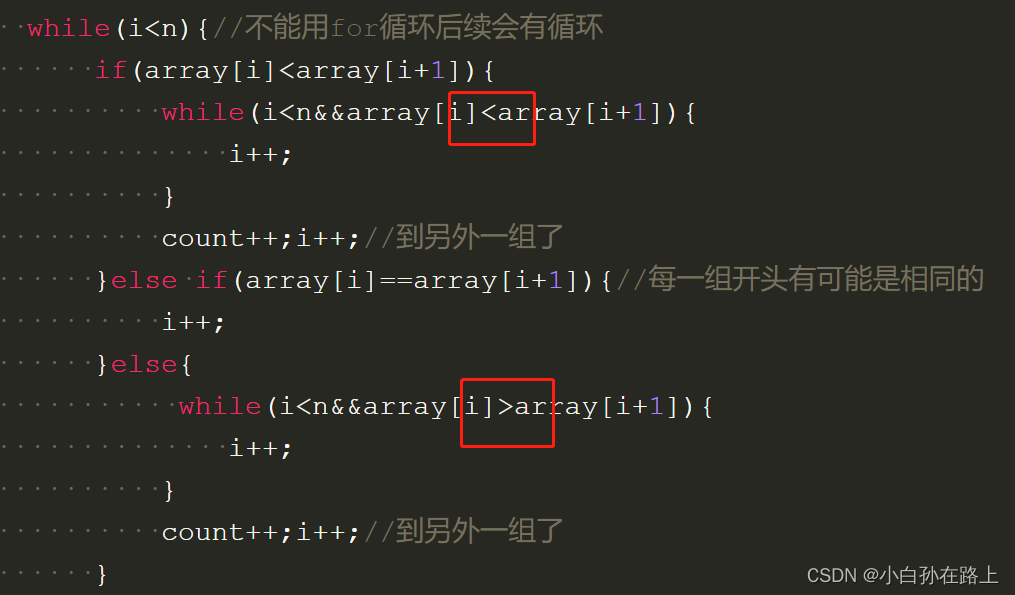
        while(i<n){//不能用for循环后续会有循环
            if(i<n&&array[i]<array[i+1]){
                while(array[i]<=array[i+1]){
                    i++;
                }
                count++;i++;//到另外一组了
            }else if(array[i]==array[i+1]){//每一组开头有可能是相同的
                i++;
            }else{
                 while(i<n&&array[i]>=array[i+1]){
                    i++;
                }
                count++;i++;//到另外一组了
            }
            
        }
        System.out.print(count);
    }
}

这种情况就算遇到相同的,就把归为下一组了.而我的处理就是也属于这一组.都没有毛病

七.二叉树非递归遍历

1.前序遍历

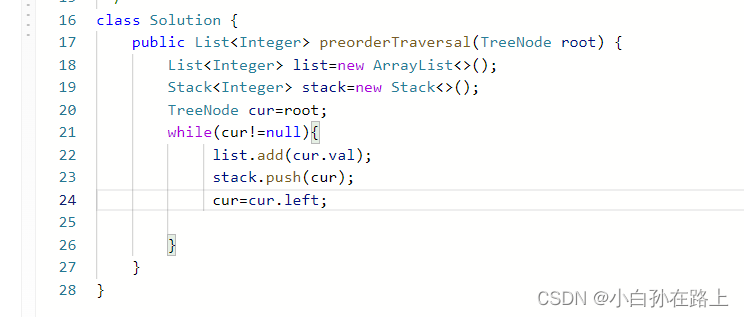
走到这一步就可能会卡.因为左边遍历完,那么右边怎么办

所以这里就展现出栈的好处了.可以到最底层的时候,cur就变成了null.就开始往回弹出元素,并打印

所以需要再嵌套一个循环

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        Stack<TreeNode> stack=new Stack<>();
        TreeNode cur=root;
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
                 list.add(cur.val);
                stack.push(cur);
                cur=cur.left;
            }
            TreeNode top=stack.pop();
          //  list.add(top.val);
            cur=top.right;
        }
        return list;
    }
}

但是有一种情况就是如果cur走到底层的右边还是null.就会跳出循环

所以循环的终止条件应该加一条栈是否为空,如果栈也为空了.就说明真的终止了

2.中序遍历

中序遍历根前序类似

只要更改打印位置即可.让他走到最左边的时候打印.然后栈往回弹的时候分别打印,再判断右是否有,有的话就打印,没有直接往回弹;

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        Stack<TreeNode> stack=new Stack<>();
        while(root!=null||!stack.isEmpty()){
            while(root!=null){
                stack.add(root);
                root=root.left;
            }
           TreeNode top=stack.pop();
           list.add(top.val);
           if(top.right!=null){
               root=top.right;
           }
        }
        return list;

    }
}

3.后续遍历

后序比较麻烦,因为如果按之前的改一下打印顺序

就会在一种情况下进行死循环

所以我们要判断是否遍历过了.就算右边是空的,但是遍历过了,就直接往后弹了

就需要建立一个后继节点来记录上次弹的元素

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        Stack<TreeNode> stack=new Stack<>();
        TreeNode prev=null;
        while(root!=null||!stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root=root.left;
            }
           TreeNode top=stack.peek();
           if(prev==top.right||top.right==null){
                stack.pop();
               list.add(top.val);
              prev=top;
           }else{
              root=top.right;
           }
        }
        return list;

    }
    
}