这篇笔记记录二叉树相关的常考题。
1 BST树区间元素搜索问题
**解决方法:**利用BST树的中序遍历,中序遍历后输出的是从小到大的顺序。
// 求满足区间的元素值 [i,j];
void findValues(vector<T> &vec, int i, int j)
{
// 封装一个递归接口
findValues(root_, vec, i, j);
}
void findValues(Node *node, vector<T> &vec,int i,int j)
{
if (node != nullptr)
{
if (node->data_ > i) // BAT中当前节点值大于左子树中任何一个值,所以,当前节点的值小于区间下界不用访问;
{
findValues(node->left_, vec, i, j);
}
// V
if (node->data_ >= i && node->data_ <= j)
{
vec.push_back(node->data_); // 存储满足区间元素的值
}
// 当前节点的右子树中。
// BST树中当前节点的值小于右子树中的值;
// 所以如果当前值区间上届j,所以当前节点小于j才访问,大于则不访问
if (node->data_ < j)
{
findValues(node->right_, vec, i, j);
}
}
}
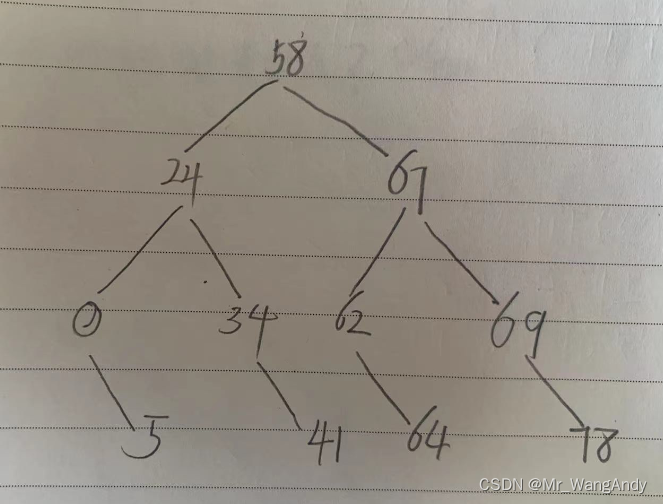
2 判断二叉树是否是一颗BST树
这道题根据BST树的定义:
BST树称为一颗搜索树或者二叉排序树,它或者是一颗空树;或者具有下列性质:
1 、若左子树不为空,则左子树上所有节点的值均小于它的根节点的值
2 、若右子树不为空,则右子树上所有节点的值均大于它的根节点的值
3 、左右子树也分别满足二叉搜索树性质
特点 :每一个节点都满足 左孩子的值(不为空) < 父节点的值 < 右孩子的值(不为空)
bool isBSTree()
{
Node *pre = nullptr;
return isBSTree(root_, pre);
}
/*
* 功能:判断二叉树是否为BST树
* 思想:利用BST中序遍历后,按照升序的顺序。
* 参数:
* node: 当前处理的节点
* &pre: 传递当前节点的引用
*/
bool isBSTree(Node *node, Node *&pre)
{
if (node == nullptr)
{
return true;
}
if (!isBSTree(node->left_, pre)) // 如果当前节点的左孩子节点与前序
{
return false;
}
if (pre != nullptr) // 根节点的pre无法确认,所以判断根节点的pre是否为空
{
if (comp_(node->data_, pre->data_))
{
return false;
}
}
pre = node; // 更新中序遍历的前驱节点
return isBSTree(node->right_, pre);
}
3 BST求子树问题
思想:先从大树中找到子树中的根节点,然后依次判断小树种根节点的左右子树。
bool isChildTree(BSTree<T, Comp> & child)
{
// 在当前二叉树找child根节点
if (child.root_ == nullptr)
{
return true;
}
Node *cur = root_;
// 这个循环是为了在大树中找到与小树根节点相同的根节点
while (cur != nullptr)
{
if (cur->data_ == child.root_->data_)
{
break;
}
else if (comp_(cur->data_,child.root_->data_))
{
cur = cur->right_;
}
else
{
cur = cur->left_;
}
}
if (cur == nullptr)
{
return false;
}
return isChildTree(cur, child.root_);
}
/*
* 功能:判断小树是否为大树的子树
*
* 参数:
* father: 大树中的节点
* child : 小树中的节点
*/
bool isChildTree(Node *father, Node *child)
{
if (father == nullptr && child == nullptr) // 如果孩子节点和父节点都是空
{
return true;
}
if (father == nullptr) // 如果只有父节点是空,说明大树中不包含小树
{
return false;
}
if (child == nullptr)
{
return true;
}
// 判断大树与小树的根节点是否相同
if (father->data_ != child->data_)
{
return false;
}
//return isChildTree(father->left_, child->left_) && isChildTree(father->right_, child->right_);
if (isChildTree(father->left_, child->left_) && isChildTree(father->right_, child->right_))
{
return true;
}
else
{
return false;
}
}
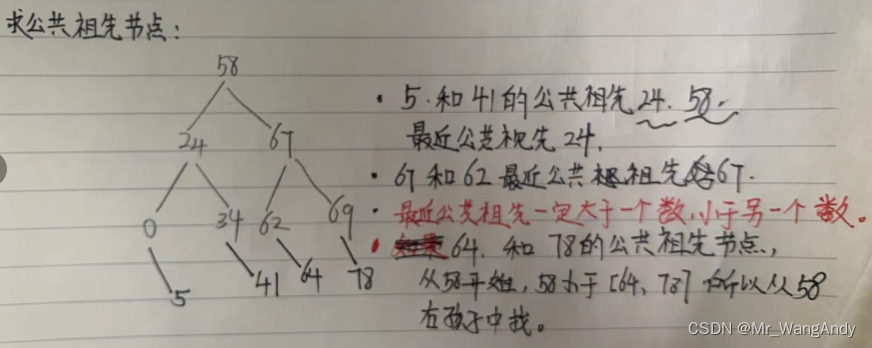
4 BST的LCA(least Comment Ancestors,最近公共祖先问题) 问题:求寻找最近公共祖先节点
公共节点判断:如果当前节点介于val1和val2之间,就认为是LCA;
/*
* 功能:最近公共祖先节点
*
* 参数:
* val1: 二叉树中的节点1
* val2: 二叉树中的节点2
*/
int getLCA(int val1, int val2)
{
Node * node = getLCA(root_, val1, val2);
if (node == nullptr)
{
throw "no LCA";
}
else
{
return node->data_;
}
} }
}
Node * getLCA(Node *node,int val1,int val2)
{
if (node == nullptr)
{
return nullptr;
}
// 如果当前节点 小于两个节点
if (comp_(node->data_, val1) && comp_(node->data_, val2))
{
return getLCA(node->right_, val1, val2);
}
else if (comp_(val1, node->data_) && comp_(val2, node->data_))
{
return getLCA(node->left_, val1, val2);
}
else
{
return node;
}
}
5 二叉树镜像对称问题
思想:node1的左孩子节点与node2的右孩子节点相同;node2的左孩子节点与node1的右孩子节点相同。
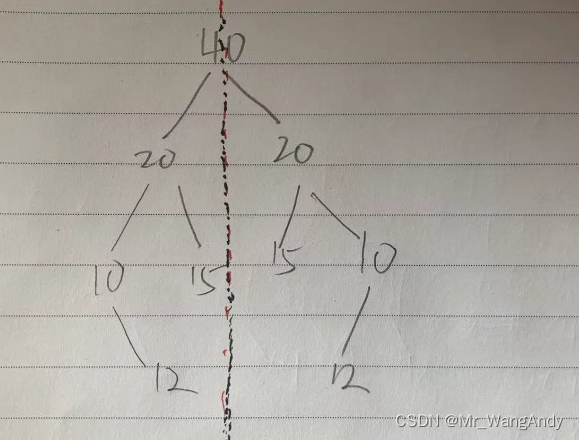
bool mirror02(Node *node1, Node *node2)
{
if (node1 == nullptr && node2 == nullptr)
{
return true;
}
if (node1 == nullptr || node2 == nullptr) // 如果有一个不对称,则认为是非对称的。
{
return false;
}
if (node1->data_ != node2->data_)
{
return false;
}
// 同时满足,一个node1的左孩子等于node2的右孩子,node2的右孩子等于node1的左孩子
return mirror02(node1->left_, node2->right_) && mirror02(node1->right_, node2->left_);
}
6 根据前序和中序重构二叉树
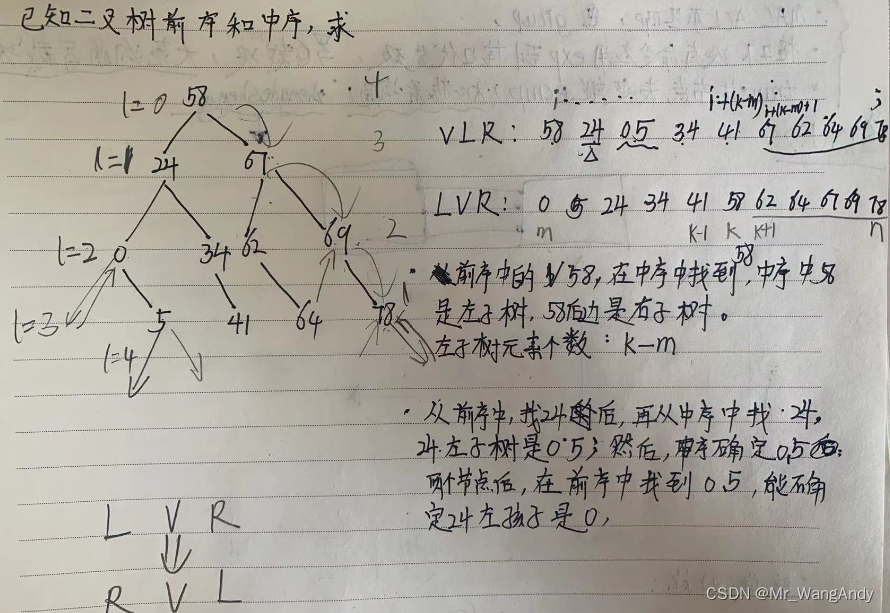
/* 功能:根据前序中序序列,构建二叉树
*
* 参数:
* pre: 前序遍历序列
* i : 前序序列中的开始索引 , i+1 --- i + (k-m) 左子树中的节点
* j : 前序序列中的末尾索引 i + (k-m)+1 --- j 右子树的节点
* in :中序遍历序列 , k表示中序序列中根节点的索引下标。
* m : 中序序列中的开始索引 m --- k-1:中序左子树中节点
* n : 中序序列中的末尾索引 k+1 --- n : 中序右子树中节点
*/
Node * _rebuild(int pre[], int i, int j,int in[], int m, int n)
{
if (i > j || m > n)
{
return nullptr;
}
// 递归时候只需考虑当前节点以及当前节点的左右孩子节点。
Node *node = new Node(pre[i]); // 先根据pre序列中的第一个i节点,创建新树的根节点。
for (int k = m; k <= n; ++k) // 在中序中找根节点的左右孩子
{
if (pre[i] == in[k]) // 在中序中找子树根节点的下标k;
{
node->left_ = _rebuild(pre, i + 1, i + (k - m),in, m, k - 1);
node->right_ = _rebuild(pre, i + (k - m) + 1, j, in, k + 1, n);
return node;
}
}
return node;
}
7 判断一颗二叉树是否为平衡二叉树
平衡: 任意节点的左右子树高度差,不能查过1 (0 1 -1 )
什么时候检测呢?递归回溯的时候;
/* 功能:判断一颗二叉树是否平衡二叉树
*
* 参数:
* node: 节点
* l : 记录层数
* flag: 记录是否平衡二叉树
*/
int isBalance(Node *node, int l, bool &flag)
{
if (node == nullptr)
{
return l;
}
int left = isBalance02(node->left_, l + 1, flag);
int right = isBalance02(node->right_, l + 1, flag);
if (abs(left - right) > 1)
{
flag = false;
}
return max(left, right);
}
8 二叉树镜像翻转问题
问题描述:求镜子中的二叉树。
思想:递归处理遍历节点时候,交换根节点的左右节点。
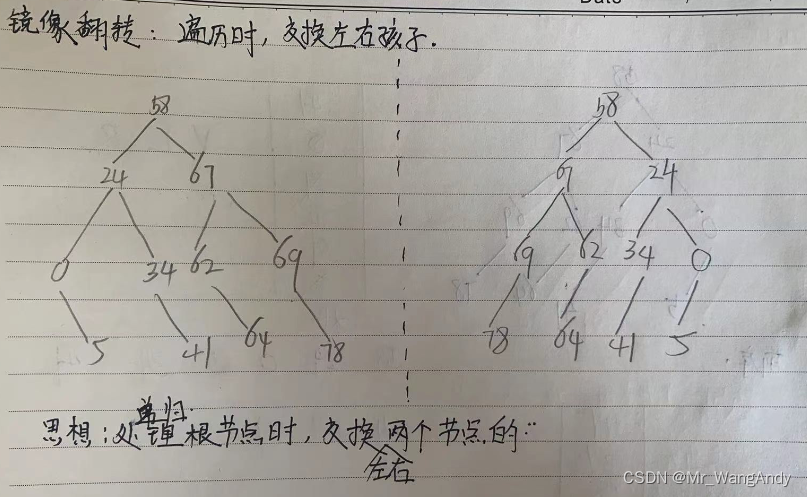
/* 功能:求镜子中的二叉树
* 思想:节点的左右孩子交换位置
* 参数:
* Node: 当前节点
*/
void mirror01(Node *node)
{
if (node == nullptr)
{
return;
}
// 处理V节点
Node *tmp = node->left_;
node->left_ = node->right_;
node->right_ = tmp;
mirror01(node->left_);
mirror01(node->right_);
}
9 求中序遍历倒数第K个节点
思想:将中序遍历LVR 转为 RVL,将求倒数第K个节点转为在RVL中求正数第k个节点
/* 功能:求中序倒数第K个节点
* 思想:将中序遍历LVR 转为 RVL,将求倒数第K个节点转为在RVL中求正数第k个节点
* 参数:
* node : 节点
* k : 找到正数第K个元素
*/
int i = 1;
Node *getVal(Node * node, int k)
{
if (node == nullptr)
{
return nullptr;
}
Node *right = getVal(node->right_, k); // R
if (right != nullptr) // V
{
return right;
}
if (i++ == k)
{
return node;
}
return getVal(node->left_, k); // L
}