目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

如果3个正整数(a,b,c)满足a^2 + b^2 = c^2的关系，则称(a,b,c)为勾股数（著名的勾三股四弦五），

为了探索勾股数的规律，我们定义如果勾股数(a,b,c)之间两两互质（即a与b，a与c，b与c之间均互质，没有公约数），则其为勾股数元组（例如(3,4,5)是勾股数元组，(6,8,10)则不是勾股数元组）。

请求出给定范围[N,M]内，所有的勾股数元组。

输入描述

起始范围N，1 <= N <= 10000

结束范围M，N < M <= 10000

输出描述

1. a,b,c请保证a < b < c,输出格式：a b c；

2. 多组勾股数元组请按照a升序，b升序，最后c升序的方式排序输出；

3. 给定范围中如果找不到勾股数元组时，输出”NA“。

用例

输入	1 20
输出	3 4 5 5 12 13 8 15 17
说明	[1,20]范围内勾股数有：(3 4 5)，(5 12 13)，(6 8 10)，(8 15 17)，(9 12 15)，(12 16 20)； 其中，满足(a,b,c)之间两两互质的勾股数元组有：(3 4 5)，(5 12 13)，(8 15 17); 按输出描述中顺序要求输出结果。

输入	5 10
输出	NA
说明	[5,10]范围内勾股数有：(6 8 10)； 其中，没有满足(a,b,c)之间两两互质的勾股数元组； 给定范围中找不到勾股数元组，输出”NA“

题目解析

本题首先需要找出给定区间内的所有勾股数，当找出勾股数后，继续判断勾股数两两之间是否互质，若否，则丢弃，若是，则保留。

最终保留的就是勾股数元组。

因此本题难点有二：1、如何找出所有勾股数； 2、如何判断两个数互质

关于1，我们可以先求出区间[n,m]的所有数的平方，缓存到一个数组arr中，然后对该数组进行双重for遍历，外层遍历所有元素arr[i]，内层遍历i之后的每一个元素arr[j]，我们求arr[i]+arr[j]的和sum，看arr中是否包含sum元素，若是，则就得到一组勾股数sqrt(arr[i])、sqrt(arr[j])、sqrt(sum)。

按照上面逻辑求得所有勾股数。

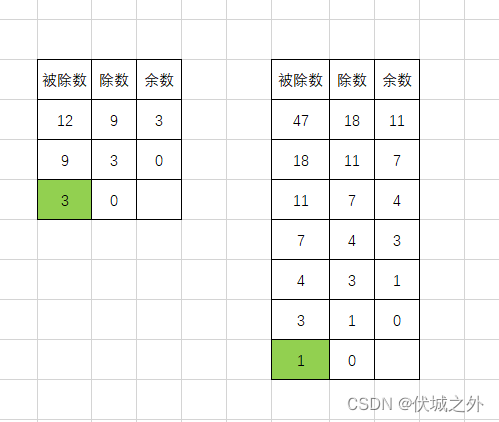
之后，我们可以根据辗转相除法判断两个数是否互质，比如求9和12是否互质，以及求47和18是否互质。

我们只需要用

a % b 得到一个 mod

然后将

a <= b

b <= mod

如果进行到b===0时，则看此时a的值，若a===1，则说明初始时的a,b互质，否则就有最大公约数结束时的a。

如下图所示：

 

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 2) {
    const [n, m] = lines.map(Number);

    getResult(n, m);

    lines.length = 0;
  }
});

function getResult(n, m) {
  const arr = [];

  for (let i = n; i <= m; i++) {
    arr.push(i * i);
  }

  const set = new Set(arr);

  const res = [];
  for (let i = 0; i < arr.length; i++) {
    for (let j = i + 1; j < arr.length; j++) {
      /* 判断勾股数 a^2 + b^2 = c^2 */
      const sum = arr[i] + arr[j];
      if (set.has(sum)) {
        res.push([Math.sqrt(arr[i]), Math.sqrt(arr[j]), Math.sqrt(sum)]);
      }
    }
  }

  const ans = res.filter((group) => {
    const [a, b, c] = group;
    return (
      isRelativePrime(a, b) || isRelativePrime(a, c) || isRelativePrime(b, c)
    );
  });

  if (!ans.length) return console.log("NA");

  ans.forEach((g) => console.log(g.join(" ")));
}

/* 判断两个数是否互质，辗转相除 */
function isRelativePrime(x, y) {
  while (y > 0) {
    let mod = x % y;
    x = y;
    y = mod;
  }

  return x === 1;
}