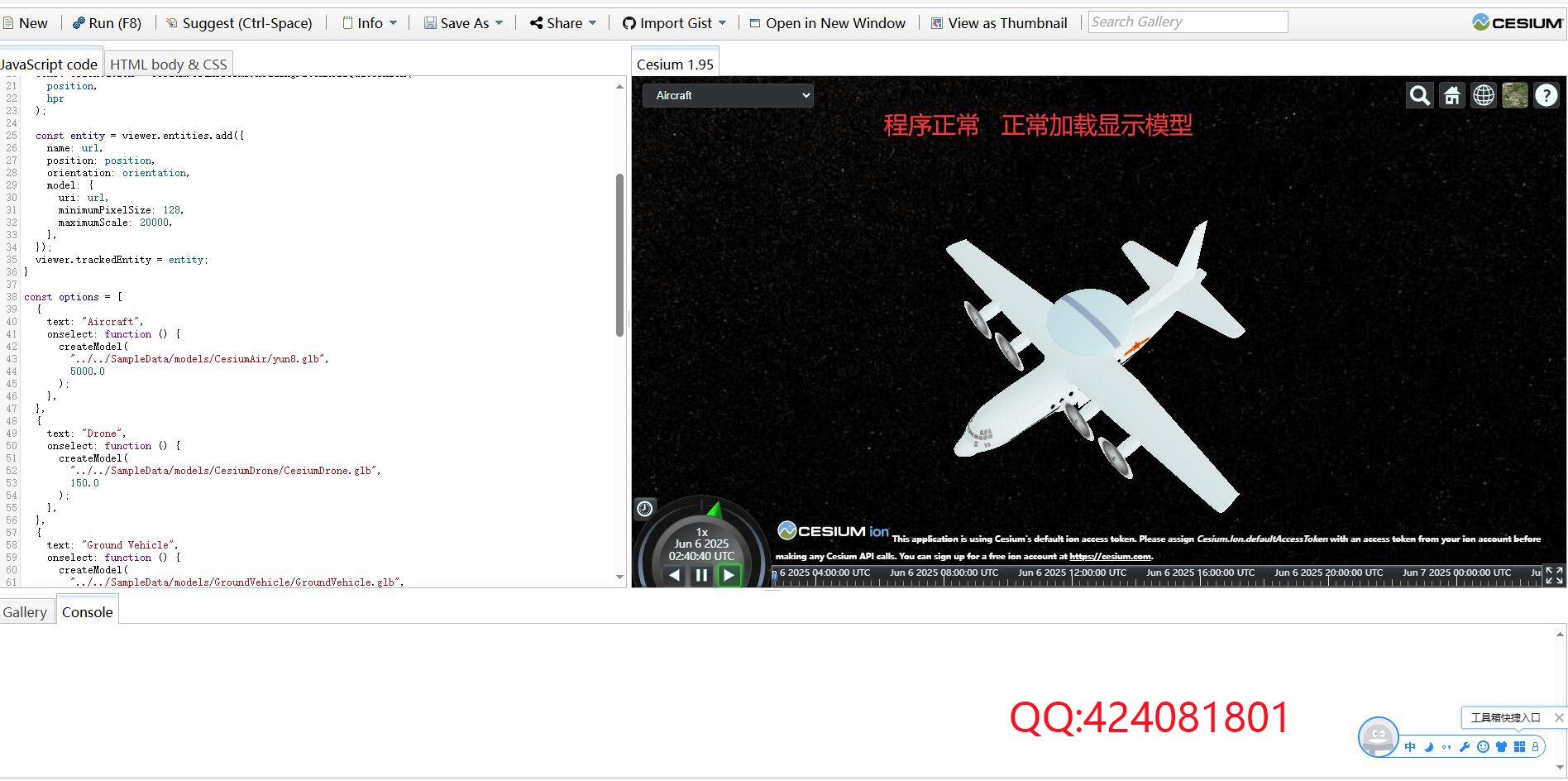
Day 62

题目描述

做法

此题本质是一个图论问题，对于两个字母相除是否存在值，其实就是判断，从一个字母能否通过其他字母到达，做法如下：

1. 遍历所有等式，为每个变量分配唯一的整数索引。
2. 初始化一个二维数组 graph，其中 graph[i][j] 表示变量 i 除以变量 j 的比值。
3. 对于每个等式 a/b = v，设置 graph[a][b] = v 和 graph[b][a] = 1/v。
4. 每个变量自身的比值为 1.0，即 graph[i][i] = 1.0。
5. 对于每个查询 a/b，检查变量是否存在于映射中。如果存在，使用 DFS 查找从 a 到 b 的路径，并计算路径上的比值乘积。如果路径不存在，返回 -1.0。

class Solution {
    public double find(double[][] graph, int x, int y, boolean[] visited) {//判断x到y是否可达
        if (graph[x][y] != 0) {
            return graph[x][y];//直接可达
        }
        visited[x] = true;
        for (int i = 0; i < graph.length; i++) {
            if (graph[x][i] != 0 && !visited[i]) {
                double p = find(graph, i, y, visited);
                if (p != 0.0) {
                    return p * graph[x][i];
                }
            }
        }
        return 0;
    }

    public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
        Map<String, Integer> num = new HashMap<>();//字符串到数字序号的转换
        int x = 0, y = 0;
        String a, b;
        for (int i = 0; i < equations.size(); i++) {
            a = equations.get(i).get(0);
            b = equations.get(i).get(1);
            if (!num.containsKey(a)) {
                num.put(a, x);
                x++;
            }
            if (!num.containsKey(b)) {
                num.put(b, x);
                x++;
            }
        }
        double[][] graph = new double[x][x];
        for (int i = 0; i < equations.size(); i++) {
            a = equations.get(i).get(0);
            b = equations.get(i).get(1);
            x = num.get(a);
            y = num.get(b);
            graph[x][y] = values[i];//x/y
            graph[y][x] = 1 / values[i];//y/x
        }
        for (int i = 0; i < graph.length; i++) {
            graph[i][i] = 1.0;//对角线全为1
        }
        //图初始化结束
        double[] res = new double[queries.size()]; //结果集合
        double sum = 0.0;
        for (int i = 0; i < queries.size(); i++) {
            a = queries.get(i).get(0);
            b = queries.get(i).get(1);
            if (!num.containsKey(a) || !num.containsKey(b)) {
                res[i] = -1.0;
                continue;
            }
            x = num.get(a);
            y = num.get(b);
            boolean[] visited = new boolean[graph.length];
            sum = find(graph, x, y, visited);//判断x到y是否可达
            if (sum == 0) {
                //不可达
                sum = -1.00000;
            }
            res[i] = sum;
            sum = 0.0;
        }
        return res;
    }
}