机器学习算法时间复杂度解析：为什么它如此重要？

news2025/7/28 6:26:12

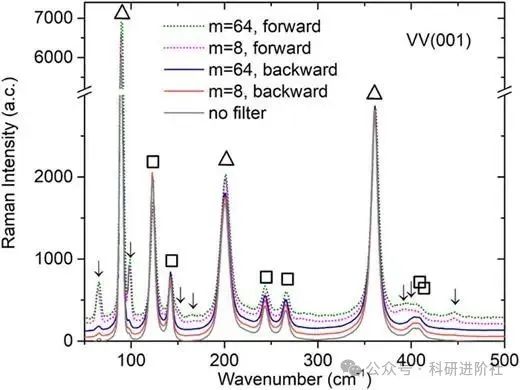
时间复杂度的重要性

虽然scikit-learn等库让机器学习算法的实现变得异常简单（通常只需2-3行代码），但这种便利性往往导致使用者忽视两个关键方面：

算法核心原理的理解缺失
忽视算法的数据适用条件

典型算法的时间复杂度陷阱

SVM：训练时间呈 $O(n^3)$ 增长，样本量过万时计算代价急剧上升
t-SNE： $O(n^2)$ 的时间复杂度使其难以处理大规模数据集

时间复杂度带来的深层理解

分析运行时行为能帮助我们：

掌握算法端到端的工作机制
预判算法在不同数据规模下的表现
做出更合理的实现选择（如kNN中优先队列比排序更高效）

关键算法的时间复杂度分析

线性模型

1. Linear Regression (OLS)

训练时间复杂度： $O(nm^2 + m^3)$

$nm^2$ ：来自计算 $X^TX$ 矩阵（ $n \times m$ 矩阵乘法）
$m^3$ ：来自对 $m \times m$ 矩阵求逆运算

推理时间复杂度： $O(m)$

只需计算 $w^Tx$ （权重向量与特征向量的点积）

2. Linear Regression (SGD)

训练时间复杂度： $O(n_{\text{epoch}}nm)$

每epoch处理 $n$ 个样本，每个样本计算 $m$ 维梯度
相比OLS省去了矩阵运算，适合大规模数据
收敛速度：通常需要更多epoch达到相同精度
每次迭代只需计算单个样本的梯度

推理时间复杂度： $O(m)$

适合大规模数据，但需要调参（学习率、迭代次数）

逻辑回归

3. Logistic Regression (Binary)

训练时间复杂度： $O(n_{\text{epoch}}nm)$

与线性回归SGD类似，但：
- 需要计算sigmoid函数
- 通常需要更多迭代收敛

推理时间复杂度： $O(m)$

4. Logistic Regression (Multiclass OvR)

训练时间复杂度： $O(n_{\text{epoch}}nmc)$

$c$ 为类别数，需要训练 $c$ 个二分类器

推理时间复杂度： $O(mc)$

类别数增加会线性增加计算成本

树模型

5. Decision Tree

训练时间复杂度： $O(mn\log(n))$

分割选择：对 $m$ 个特征各需 $O(n)$ 计算
树深度：平衡树约 $\log(n)$ 层
对于平衡树，每层需要 $O(mn)$ 时间，共 $log(n)$ 层

推理时间复杂度： $O(d_{\text{tree}})$

对特征缩放不敏感，适合类别特征
只需从根节点遍历到叶节点

6. Random Forest Classifier

训练时间复杂度： $O(n_{\text{tree}} mn\log(n))$

$t$ 棵树的独立训练（可并行）
特征采样：实际 $m$ 可能减小

推理时间复杂度： $O(n_{\text{tree}}d_{\text{tree}})$

可通过并行化加速训练，但内存消耗大
需要所有树的投票

其他关键算法

7. Support Vector Machines

训练时间复杂度： $O(n^2m+n^3)$

取决于核函数和优化算法

推理时间复杂度： $O(mn_{\text{SV}})$ （sv为支持向量数）

大数据集性能差，适合小规模高维数据
只依赖支持向量

8. K-Nearest Neighbors

训练时间复杂度： $O(1)$

仅存储训练数据

推理时间复杂度： $O(nm)$

推理慢但训练快，适合低维数据

9. Naive Bayes

训练时间复杂度： $O(nm)$

只需计算特征统计量

推理时间复杂度： $O(cm)$

线性复杂度，适合文本分类等高维数据
对 $c$ 个类别计算联合概率

10. Principal Component Analysis

训练时间复杂度： $O(nm^2+m^3)$

来自协方差矩阵特征分解
大数据优化：可用随机SVD
特征数很大时计算成本高

11. t-SNE

训练时间复杂度： $O(n^2m)$

成对相似度计算占主导
内存瓶颈：需要存储 $n \times n$ 矩阵
难以扩展到大规模数据

推理时间复杂度：不适用（通常只用于可视化）

12. KMeans Clustering

训练时间复杂度： $O(knim)$

每次迭代计算所有点到 $k$ 中心的距离
Lloyd算法：线性收敛但可能陷入局部最优

推理时间复杂度： $O(km)$

实践建议

大数据集：优先考虑线性时间复杂度算法
高维数据：注意维度对距离计算的影响
模型选择：不仅要考虑准确率，还要评估计算成本

理解这些时间复杂度特性，能帮助你在实际项目中做出更明智的算法选择，避免在大型数据集上遭遇性能瓶颈。

扩展阅读

线性模型选择中容易被忽视的关键洞察-CSDN博客
不会选损失函数？16种机器学习算法如何“扣分”？-CSDN博客
10 个最常用的损失函数-CSDN博客

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2403287.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！