题目描述

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

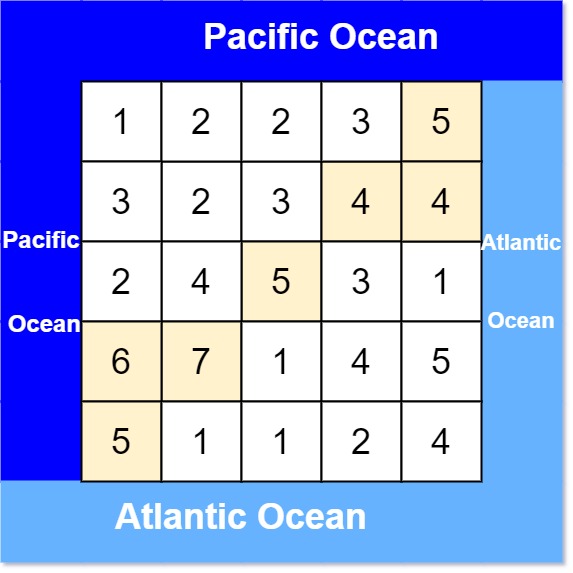
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

• m == heights.length
• n == heights[r].length
• 1 <= m, n <= 200
• 0 <= heights[r][c] <= 105

解决方案：

1、分析问题求解：水从一定高度可以流向上（左）和下（右）两种边界低处，其高度不一定是最高

2、两种情况分别讨论：从上或左 || 从下或右

3、逆向思维：从低处到高处，正向遍历，解集合：两种情况的高度都有重合即是答案

函数源码：

class Solution {
public:

    vector<int> direction{-1,0,1,0,-1};

    void dfs(vector<vector<int>>& heights,vector<vector<bool>>&reach,int row,int col){
        if(reach[row][col])     return;//结束条件：

        reach[row][col]=true;
        int x,y;
        for(int i=0;i<4;i++){
            x=row+direction[i],y=col+direction[i+1];//转化为上下左右四格的位置
            if( x>=0 && x<heights.size() && 
                y>=0 && y<heights[0].size() &&
                heights[row][col]<=heights[x][y]){
                    dfs(heights,reach,x,y);//row=x;col=y;更新位置
            }
        }

    }


    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
        if(heights.empty()||heights[0].empty())     return {};
        
        vector<vector<int>> ans;
        int row=heights.size();
        int col=heights[0].size();
        vector<vector<bool>> p(row,vector<bool>(col,false)); 
        vector<vector<bool>> a(row,vector<bool>(col,false));

        for(int i=0;i<row;i++){//左边界，右边界
            dfs(heights,p,i,0);
            dfs(heights,a,i,col-1);
        }
        for(int i=0;i<col;i++){//上边界，下边界
            dfs(heights,p,0,i);
            dfs(heights,a,row-1,i);
        }
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                if(p[i][j]&&a[i][j]){
                    ans.push_back(vector<int>{i,j});
                }
            }
        }
        
        return ans;

    }
};