Relational Algebra（数据库关系代数）

news2025/6/3 20:50:32

What is an “Algebra”

What is Relational Algebra?

Core Relational Algebra

Selection

Projection

Extended Projection

Product（笛卡尔积）

Theta-Join

Natural Join

Renaming

Building Complex Expressions

Sequences of Assignments

Expressions in a Single Assignment

Expression Trees

Example: Tree for a Query

Example: Self-Join

Operations on Bags

What is an “Algebra”

Mathematical system consisting of:

Operands --- variables or values from which new values can be constructed.（操作数，用于构建新值的变量或者值）
Operators --- symbols denoting procedures that construct new values from given values.（运算符，标志着从给定值创建新值的过程）

What is Relational Algebra?

An algebra whose operands are relations or variables that represent relations.（关系代数是操作数是关系或者是表示关系的变量）
Operators are designed to do the most common things that we need to do with relations in a database.
The result is an algebra that can be used as a query language for relations.（关系代数语言将会是数据库语言的基础）

Core Relational Algebra

Union, intersection, and difference.（并、交、差）

Usual set operations, but both operands must have the same relation schema.（两个操作数之间必须要有一样的关系模式）

Selection: picking certain rows.（也就是SQL中的WHERE）
Projection: picking certain columns.
Products and joins: compositions of relations.（笛卡尔积和连接：笛卡尔积是全组合、连接是条件组合）
Renaming of relations and attributes.

Selection

$R_{1}:=\sigma _{C}(R_{2})$

C is a condition (as in “if” statements) that refers to attributes of R2.
R1 is all those tuples of R2 that satisfy C.

这两个关系之间没有任何关系

Projection

$R_{1}:=\pi _{L}(R_{2})$

L is a list of attributes from the schema of R2.（L是R2关系模式中的一串属性）
R1 is constructed by looking at each tuple of R2, extracting the attributes on list L, in the order specified, and creating from those components a tuple for R1.（查看R2的属性列表，然后提取出L属性列表中的属性，然后按照特定顺序创建R1的元组）
Eliminate duplicate tuples, if any.（消除重复项）

Extended Projection

Using the same $\pi _{L}$ operator, we allow the list L to contain arbitrary expressions（任意表达式） involving attributes:
Arithmetic on attributes, e.g., A+B->C.
Duplicate occurrences of the same attribute.

Product（笛卡尔积）

$R_{3}:=R_{1}\times R_{2}$

Pair each tuple t1 of R1 with each tuple t2 of R2.
Concatenation t1t2 is a tuple of R3.
Schema of R3 is the attributes of R1 and then R2, in order.

But beware attribute A of the same name in R1 and R2: use R1.A and R2.A.（如果R1、R2中有相同的属性使用R1.A和R2.A来进行区分）

Theta-Join

$R_{3}:=R_{1}\bowtie _{C}R_{2}$

Take the product R1 Χ R2.
Then apply $\bowtie _{C}$ to the result.
As for σ, C can be any boolean-valued condition.（对于C来说，可以是任何布尔值的表达式）

Historic versions of this operator allowed only A $\theta$ B, where $\theta$ is = , <, etc.; hence the name “theta-join.”

Natural Join

A useful join variant (natural join) connects two relations by:
Equating（等值比较） attributes of the same name, and Projecting out one copy of each pair of equated attributes.（将等值属性的一组副本投影掉）
Denoted R3 := R1 ⋈ R2.

Renaming

The ρ operator gives a new schema to a relation.
$R_{1}:=\rho _{R1(A_{1}A_{2}...A_{n})}(R2)$ makes R1 be a relation with attributes A1,…,An and the same tuples as R2.
Simplified notation: $R1(A_{1}A_{2}...A_{n}):=R2$

Building Complex Expressions

Combine operators with parentheses and precedence rules.（通过括号或者优先运算规则对操作符进行组合）

Three notations, just as in arithmetic:

Sequences of assignment statements.
Expressions with several operators.
Expression trees.

Sequences of Assignments

Create temporary relation names.
Renaming can be implied by giving relations a list of attributes.
Example:

R3 := R1 ⋈ C R2

can be written:

R4 := R1 Χ R2

R3 := σ C (R4)

Expressions in a Single Assignment

Example:

the theta-join R3 := R1 ⋈C R2

can be written:

R3 := σC (R1 Χ R2)

Precedence of relational operators:

[σ, π, ρ] (highest).

[Χ, ⋈].

∩.

[∪, —]

Expression Trees

Leaves are operands --- either variables standing for relations or particular constant relations.（叶子结点是操作数，可以是标识关系的变量也可以是常量）
Interior nodes are operators, applied to their child or children.（内部结点是操作符，作用于子结点）

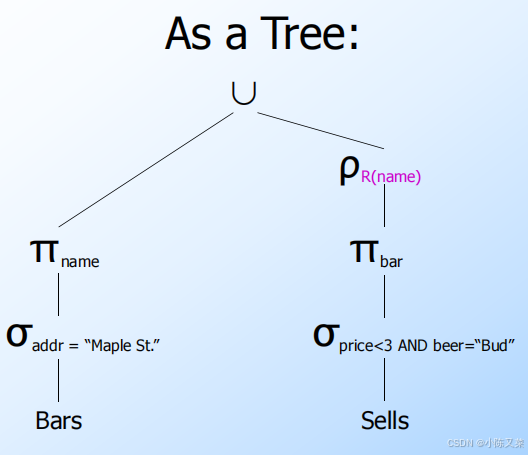
Example: Tree for a Query

Using the relations Bars(name, addr) and Sells(bar, beer, price), find the names of all the bars that are either on Maple St. or sell Bud for less than $3.

Example: Self-Join

Using Sells(bar, beer, price) , find the bars that sell two different beers at the same price.

Strategy :

by renaming, define a copy of Sells, called S(bar, beer1, price).
The natural join of Sells and S consists of quadruples (bar, beer, beer1, price)
such that the bar sells both beers at this price.

先通过重命名得到一个Sells的副本，然后将原表与副本进行自连接，自连接的条件是price相同，然后进行选择，最后投影出name

Operations on Bags

Selection applies to each tuple, so its effect on bags is like its effect on sets.
Projection also applies to each tuple, but as a bag operator, we do not eliminate duplicates.
Products and joins are done on each pair of tuples, so duplicates in bags have no effect on how we operate.